
Задача № 6
Исследовать
функцию
![]() и построить схематично её график.
и построить схематично её график.
Решение.
Областью определения данной функции являются все действительные значения аргумента
 ,
кроме тех, при которых знаменатель
дроби обращается в ноль:
,
кроме тех, при которых знаменатель
дроби обращается в ноль:
![]() ;
;
![]() .
.
![]() .
.
Определим точки пересечения графика функции с осями координат:
с осью
 график функции не пересекается, так
как
график функции не пересекается, так
как
 ;
;
с осью
 при
при
 :
:
 ;
;
 ;
;
![]() ;
;
![]() .
.
Точка
![]() – точка пересечения графика функции
с осью
.
– точка пересечения графика функции
с осью
.
Функция
 не является ни чётной, ни нечётной
так как
не является ни чётной, ни нечётной
так как
![]() и
и
![]() ,
,
![]() .
.
Определим точки возможного экстремума, то есть точки из
 ,
в которых производная
,
в которых производная
 либо не существует.
либо не существует.

![]() .
.
![]() существует при всех
существует при всех
![]() ,
то есть при
,
то есть при
![]() .
.
Точка
![]() ,
в которой
не существует, не является точкой
возможного экстремума, поскольку не
входит в область определения
функции
.
,
в которой
не существует, не является точкой
возможного экстремума, поскольку не
входит в область определения
функции
.
при
![]() ,
то есть при
,
то есть при
![]() ;
;
![]() .
.
Значит
– единственная точка возможного
экстремума, которая разбивает
![]() на три интервала:
на три интервала:
![]() ,
,
![]() и
и
![]() .
.
Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:
-

+
–
0
+
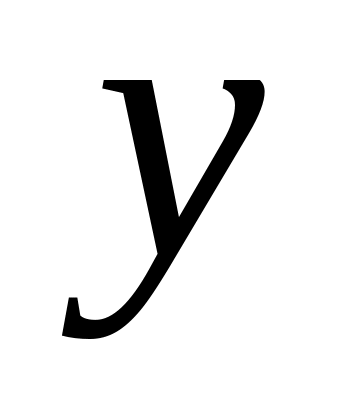

Функция убывает при
![]() и возрастает при
и возрастает при
![]() .
.
При переходе через точку меняет знак, значит функция имеет экстремум в точке .
При переходе через точку меняет знак с «–» на «+», значит является точкой минимума функции.
![]() ,
,
![]() .
.
Точка
![]() – точка минимума функции
.
– точка минимума функции
.
Определим точки возможного перегиба, то есть точки из , в которых вторая производная либо не существует.
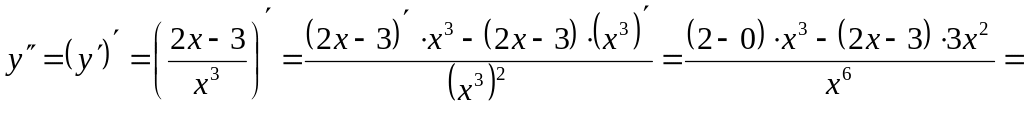
![]() .
.
![]() существует при всех
,
то есть при
существует при всех
,
то есть при
![]() .
.
Точка , в которой не существует, не является точкой возможного перегиба, поскольку не входит в область определения функции .
при
![]() ,
то есть при
,
то есть при
![]() ;
;
![]() ;
;
![]() .
.
Значит
– единственная точка возможного
перегиба, которая разбивает
на три интервала:
,
![]() и
и
![]() .
.
Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:
-
х

+
+
0
–
у



При
![]() график функции вогнутый, а при
график функции вогнутый, а при
![]() – выпуклый.
– выпуклый.
При переходе через точку меняет знак, значит график функции имеет перегиб в точке .
![]() ,
,
![]() .
.
Точка
![]() – точка перегиба графика функции
.
– точка перегиба графика функции
.
Функция непрерывна на своей области определения, то есть при .
В точке функция не определена, а значит имеет разрыв.
Предел слева
![]() ,
,
предел справа
![]() ,
,
значит – точка разрыва 2-го рода.
Исследуем функцию на наличие у её графика асимптот.
Прямая является вертикальной асимптотой графика функции , так как – точка разрыва 2-го рода.
Проверим наличие у графика функции невертикальных (наклонных, горизонтальных)
асимптот вида
![]() ,
где
,
где
![]() ,
,
![]() .
.
 ;
;
![]() ,
,
следовательно, прямая
![]() ,
то есть прямая
,
то есть прямая
![]() ,
совпадающая с осью
,
является горизонтальной асимптотой
графика функции
.
,
совпадающая с осью
,
является горизонтальной асимптотой
графика функции
.
Строим график функции , нанеся предварительно на плоскость найденные точки , и , а также асимптоты – прямую , совпадающую с осью , и прямую , совпадающую с осью .
Кроме того, возьмём для уточнения дополнительную точку:
![]() ,
тогда
,
тогда
![]() .
Точка
.
Точка
![]() .
.

|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
-4 |
|
-3 |
|
-2 |
|
-1 |
|
О |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНТРОЛЬНУЮ РАБОТУ № 2 ВАРИАНТ 10 – можно приобрести за отдельную плату.
Цена 500 рублей.
Оплата принимается через webmoney и яндекс.деньги
(т.е. электронными деньгами или через терминалы связи)
Для покупки обращайтесь – vzfeiextra@yandex.ru
КР №2, Вар 10 (Демо версия)
Задача № 1
Найти
неопределённый интеграл:
![]() .
.
Решение.
Сделаем замену переменной:
![]() .
.
Тогда
![]() ,
откуда
,
откуда
![]() ……
……
Задача № 2
Вычислить
определённый интеграл
![]() .
.
Решение.
Сделаем замену переменной:
![]() .
.
![]() .
.
Тогда
![]() ,
…
,
…
Задача № 3
Вычислить
определённый интеграл
![]() .
.
Решение.
Воспользуемся формулой
![]() интегрирования по частям, взяв….
интегрирования по частям, взяв….
Задача № 4
Решить
дифференциальное уравнение:
![]() .
.
Решение.
Заданное уравнение является дифференциальным уравнением первого порядка…..
Задача № 5
Вычислить
площадь фигуры, ограниченной линиями
![]() ,
,
![]() .
.
Решение.
Найдём точки пересечения параболы и прямой , для чего
решим систему их уравнений: …
Задача № 6
Экспериментальные данные о значениях переменных х и у приведены в таблице:
|
1 |
1,5 |
2 |
2,5 |
3 |
|
2,2 |
3,9 |
5,8 |
8,8 |
12,3 |
В результате их выравнивания получена
функция
![]() .
Используя метод наименьших квадратов,
аппроксимировать эти данные линейной
зависимостью
.
Используя метод наименьших квадратов,
аппроксимировать эти данные линейной
зависимостью
![]() (найти параметры a
и b). Выяснить, какая
из двух линий лучше (в смысле метода
наименьших квадратов) выравнивает
экспериментальные данные. Сделать
чертёж.
(найти параметры a
и b). Выяснить, какая
из двух линий лучше (в смысле метода
наименьших квадратов) выравнивает
экспериментальные данные. Сделать
чертёж.
Решение.
В соответствии с методом наименьших
квадратов искомая линейная зависимость
имеет уравнение
![]() ,
где…
,
где…
