
Контрольная работа по математическом анализу для ВЗФЭИ по методическим указаниям 2009 года. Выполнено авторским коллективом ООО «Взфэи-архив.рф» © 2010. Avzfei.ru. Авторские права на данную работу зарегистрированы Российским авторским обществом КОПИРУС совместно с Федеральным государственным учреждением Российская государственная библиотека - РГБ.
© ООО «ВЗФЭИ-АРХИВ.РФ», 2010
Электронная версия данного текстовой работы предназначена исключительно для ознакомления. Незаконное распространение, публикация (в том числе и на интернет-ресурсах), передача третьим лицам текста данной работы, либо фрагментов текста данной работы без прямой цитаты и согласования с правообладателем преследуется по закону, а лица виновные в данных правонарушениях несут ответственность, предусмотренную главой 4 Гражданского Кодекса РФ.
Если Вы обнаружили данную работу на каком-либо сайте, кроме avzfei.ru, взфэи.su, взфэи-архив.рф – немедленно сообщите об этом на адрес электронной почты: vzfeiextra@ya.ru – Вознаграждение сообщившему гарантируется!
Вариант 2
Задача № 1
По
формулам Крамера решить систему линейных
уравнений
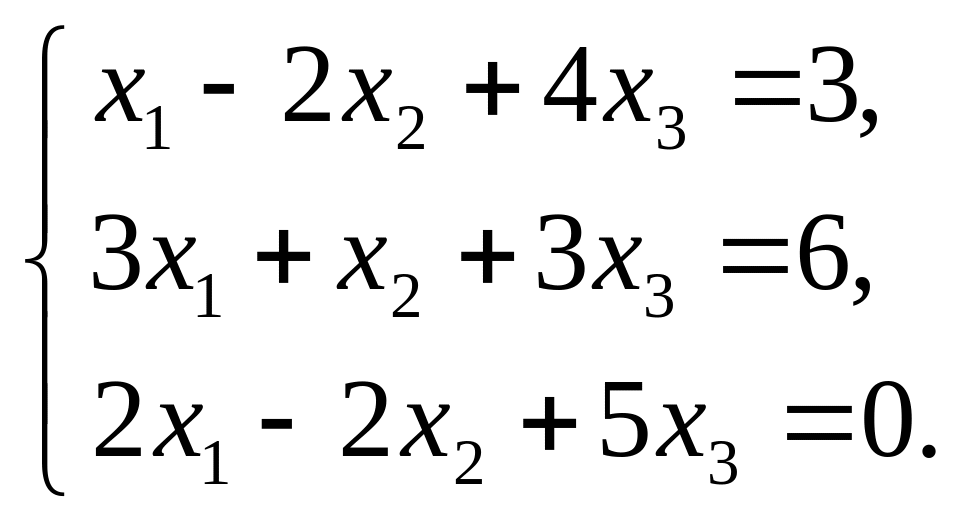
Решение.
Найдём определитель системы:
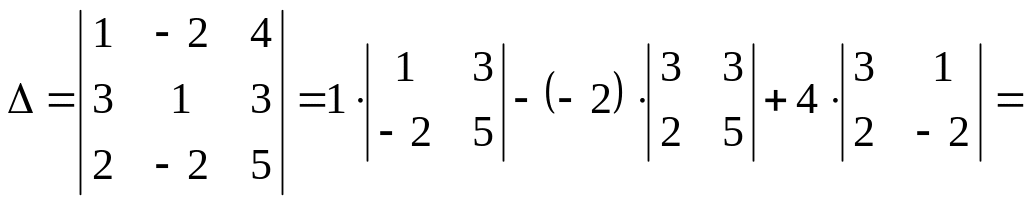
![]() .
.
![]() ,
следовательно, система имеет единственное
решение, которое можно найти по формулам
Крамера:
,
следовательно, система имеет единственное
решение, которое можно найти по формулам
Крамера:
![]() ,
,
![]() ,
,
![]() .
.
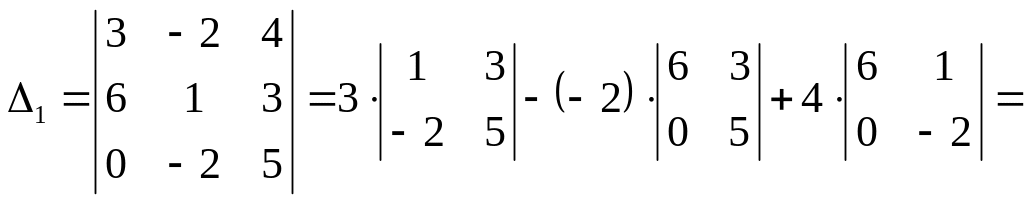
![]() ;
;
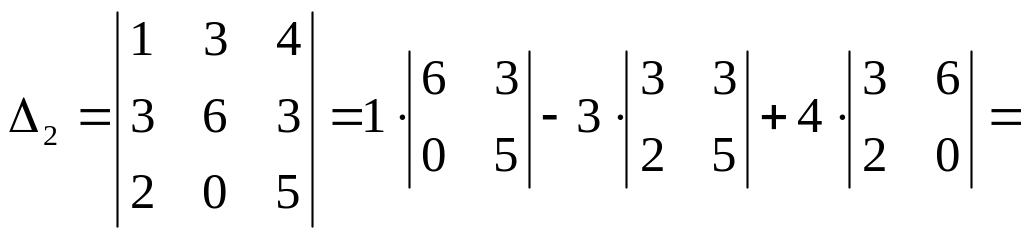
![]() ;
;
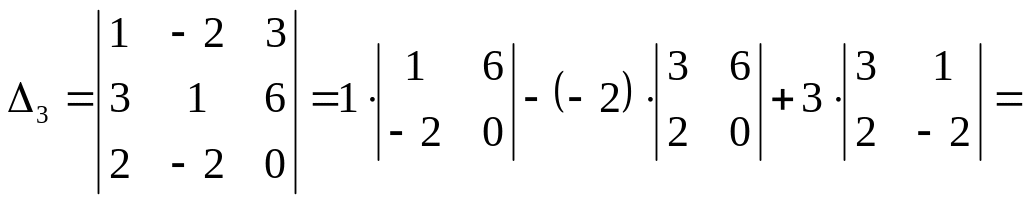
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
![]() – решение заданной системы.
– решение заданной системы.
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Задача № 2
Найти
предел
![]() .
.
Решение.
Имеем неопределённость
вида
![]() .
.
Для раскрытия
этой
неопределённости умножим и разделим
выражение в скобках на сопряжённое
выражение
![]() :
:
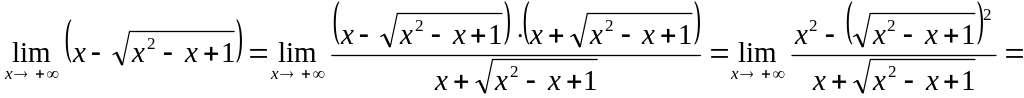
![]()

Получили
неопределённость
вида
![]() .
.
Для раскрытия этой неопределённости
вынесем за скобки в числителе и в
знаменателе дроби наивысшую степень
аргумента, то есть
![]() ,
а затем сократим дробь:
,
а затем сократим дробь:
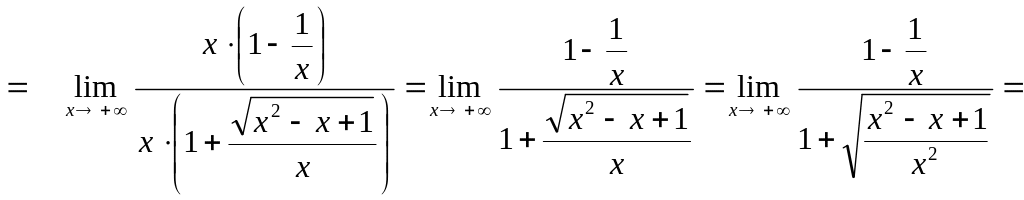
 ,
,
так как
при
![]()
![]() и
и
![]() .
.
Ответ: 0,5.
Задача № 3
Найти
производную функции
![]() .
.
Решение.
Воспользуемся свойствами производной:
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
где
,
где
![]() – константа, а также таблицей
– константа, а также таблицей
производных:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где С – константа.
,
где С – константа.

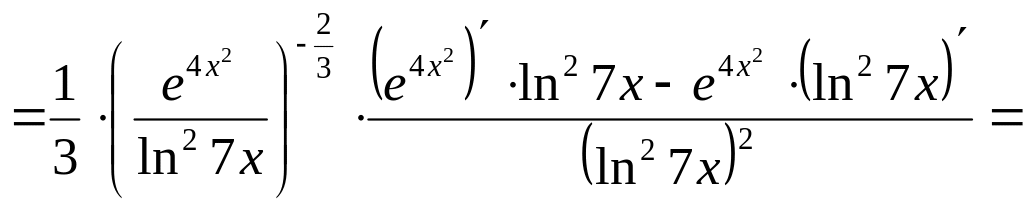
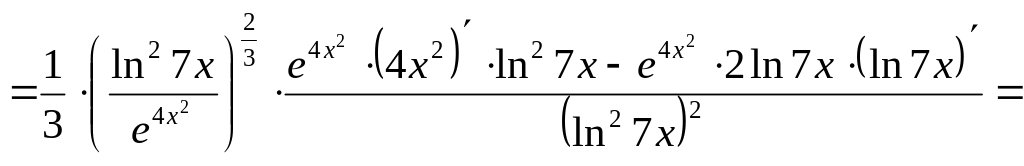
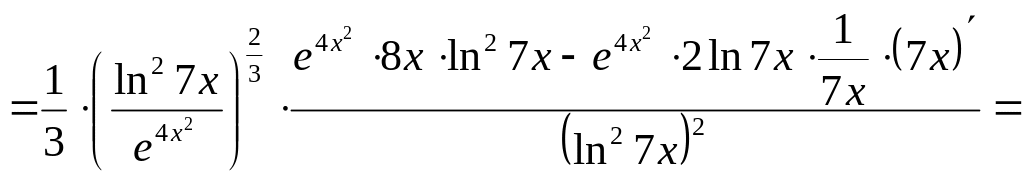
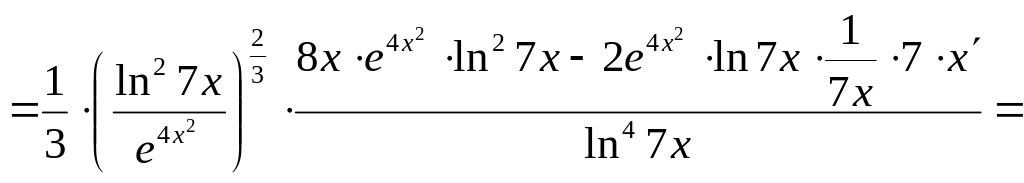
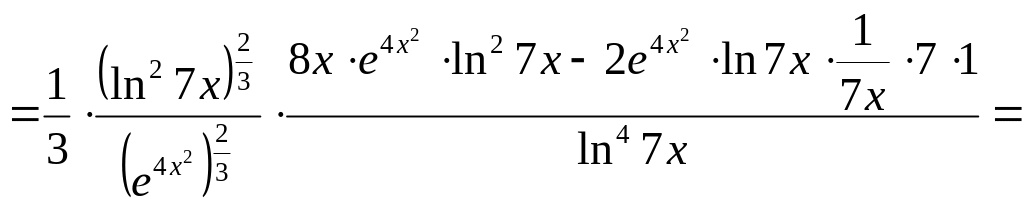
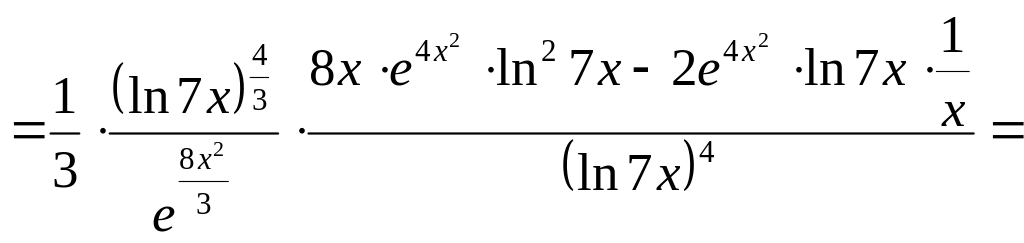
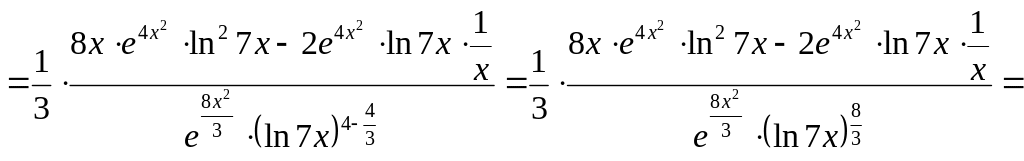
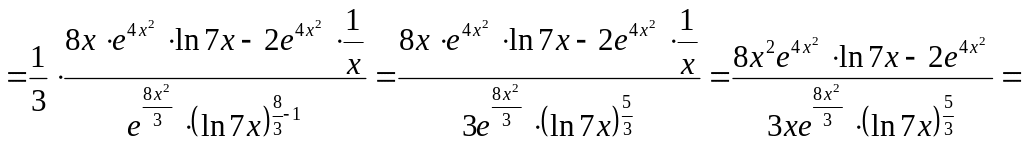

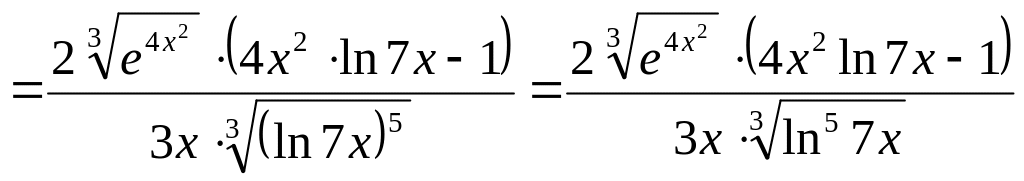 .
.
Ответ:
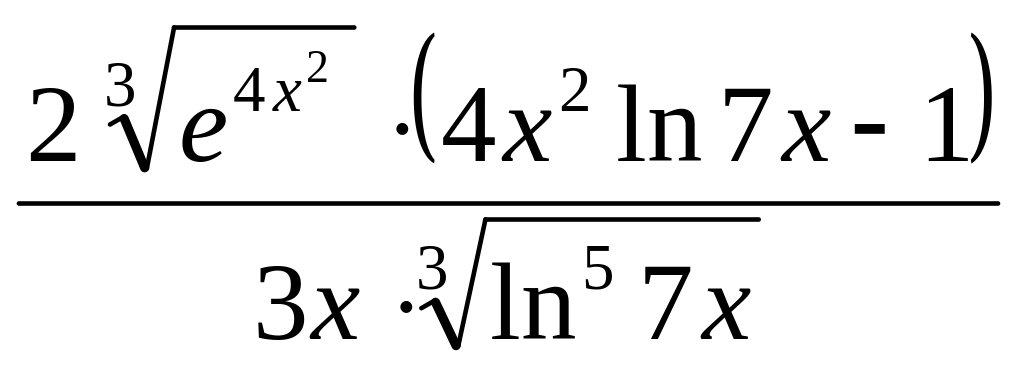 .
.
Задача № 4
Какую наибольшую площадь может иметь прямоугольный треугольник, сумма квадратов катетов которого равна 18?
Решение.
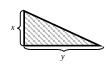
Обозначим через
и
![]() катеты прямоугольного треугольника.
катеты прямоугольного треугольника.
По условию сумма квадратов треугольника
равна 18, то есть
![]() .
Выражая из последнего равенства
,
получаем:
.
Выражая из последнего равенства
,
получаем:
![]() ;
;
![]() .
.
Очевидно,
![]() ,
следовательно,
,
следовательно,
![]() .
.
Площадь данного прямоугольного
треугольника равна произведению длин
катетов этого треугольника:
![]() .
.
Область
определения функции
![]() :
:
![]() ;
;
![]() ;
;
;
;
![]() ;
;
![]() .
.
Исследуем на экстремум функцию
![]() площади прямоугольного треугольника.
площади прямоугольного треугольника.
Определим точки возможного экстремума,
то есть точки из
![]() ,
в которых производная
,
в которых производная
![]() либо не существует.
либо не существует.
![]()
![]()
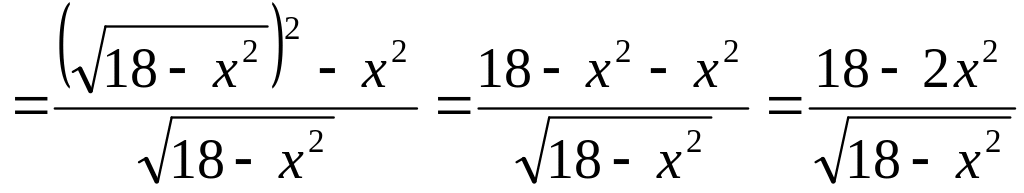 .
.
![]() существует при всех
существует при всех
![]() ,
то есть при
,
то есть при
![]() .
.
при
![]() ,
то есть при
,
то есть при
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
Значит
.
Значит
![]() – единственная точка возможного
экстремума, которая разбивает
на два интервала:
– единственная точка возможного
экстремума, которая разбивает
на два интервала:
![]() и
и
![]() .
.
Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:
-
3

+
0
–
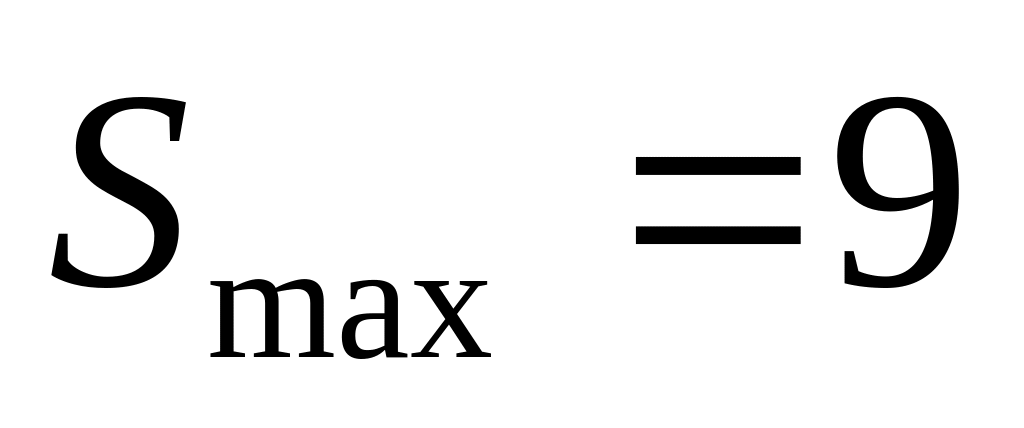

Функция
![]() возрастает при
возрастает при
![]() и убывает при
и убывает при
![]() .
.
При переходе через точку меняет знак, значит функция имеет экстремум в точке .
При переходе через точку меняет знак с «+» на «–», значит является точкой максимума функции.
![]() ,
,
![]() (кв. ед.).
(кв. ед.).
Таким образом, наибольшую площадь
![]() (кв. ед.) имеет прямоугольный треугольник
с катетами
и
(кв. ед.) имеет прямоугольный треугольник
с катетами
и
![]() ,
сумма квадратов катетов которого равна
18.
,
сумма квадратов катетов которого равна
18.
Ответ: прямоугольный треугольник, сумма квадратов катетов которого равна 18, будет иметь наибольшую площадь 9 (кв. ед.), если его катеты равны соответственно 3 и 3.
Задача № 5
Составить уравнения касательных к
графику функции
![]() ,
проведённых в точках её пересечения
с прямой
,
проведённых в точках её пересечения
с прямой
![]() .
Сделать чертёж.
.
Сделать чертёж.
Решение.
Найдём точки пересечения параболы
![]() и прямой
и прямой
![]() ,
для чего
,
для чего
решим систему их уравнений:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
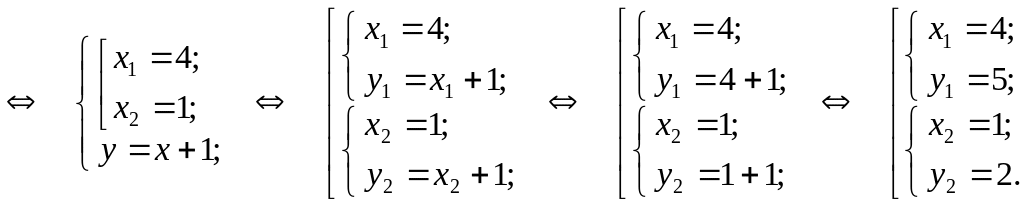
Итак, парабола
и прямая
пересекаются в двух точках:
![]() и
и
![]() .
.

|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
-6 |
|
-4 |
|
-2 |
|
О |
|
2 |
|
4 |
|
6 |
|
8 |
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение касательной к кривой
![]() в точке
в точке
![]() имеет вид
имеет вид
![]() .
.
Найдём
![]() :
:
![]() .
.
![]() ;
;
![]() .
.
Уравнение касательной к кривой в точке имеет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Уравнение касательной к кривой в точке имеет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, касательные, проведённые
к графику функции
,
в точках её пересечения с прямой
,
имеют уравнения
![]() и
и
![]() .
.
Ответ: и .
