
Контрольная работа по математическом анализу для ВЗФЭИ по методическим указаниям 2008 года. Выполнено авторским коллективом ООО «Взфэи-архив.рф» © 2010. Avzfei.ru. Авторские права на данную работу зарегистрированы Российским авторским обществом КОПИРУС совместно с Федеральным государственным учреждением Российская государственная библиотека - РГБ.
© ООО «ВЗФЭИ-АРХИВ.РФ», 2010
Электронная версия данного текстовой работы предназначена исключительно для ознакомления. Незаконное распространение, публикация (в том числе и на интернет-ресурсах), передача третьим лицам текста данной работы, либо фрагментов текста данной работы без прямой цитаты и согласования с правообладателем преследуется по закону, а лица виновные в данных правонарушениях несут ответственность, предусмотренную главой 4 Гражданского Кодекса РФ.
Если Вы обнаружили данную работу на каком-либо сайте, кроме avzfei.ru, взфэи.su, взфэи-архив.рф – немедленно сообщите об этом на адрес электронной почты: vzfeiextra@ya.ru – Вознаграждение сообщившему гарантируется!
Вариант 10
Задача № 1
Найти матрицу ●·
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение.
Для матрицы транспонированной является матрица
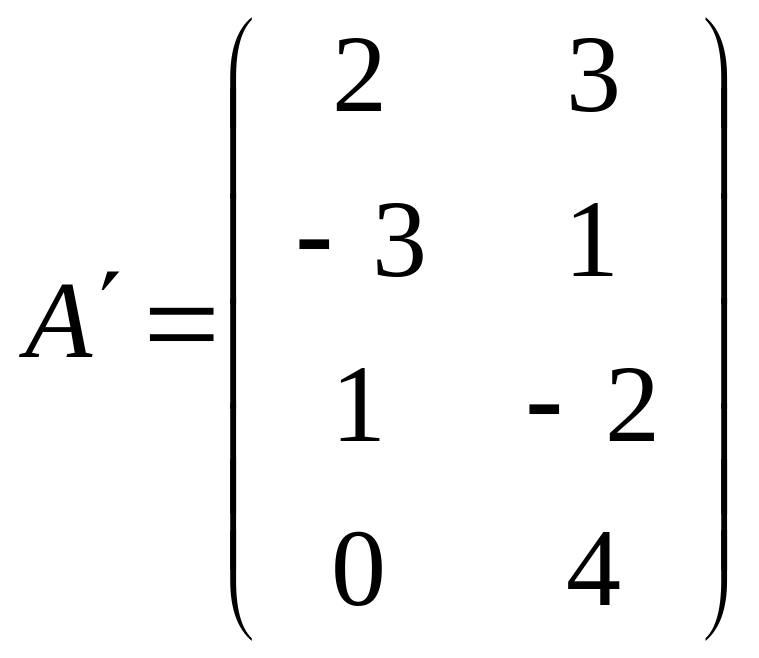 .
.
Число столбцов матрицы
![]() (равно 4) равно числу строк матрицы
(равно 4) равно числу строк матрицы
![]() ,
то есть матрица
согласована с матрицей
,
следовательно определено произведение
,
то есть матрица
согласована с матрицей
,
следовательно определено произведение
![]() .
.
Произведением матрицы
размера
![]() на матрицу
на матрицу
![]() размера
размера
![]() называется такая матрица
называется такая матрица
![]() размера
размера
![]() ,
каждый элемент которой
,
каждый элемент которой
![]() равен сумме произведений элементов
равен сумме произведений элементов
![]() -ой
строки матрицы
на соответствующие элементы
-ой
строки матрицы
на соответствующие элементы
![]() -го
столбца матрицы
:
-го
столбца матрицы
:
![]() ,
,
![]() ;
;
![]() .
.
В нашем
случае

![]() .
.
Найдём матрицу
,
где
![]() – единичная матрица:
– единичная матрица:
![]()
![]() .
.
Ответ:
![]() .
.
Задача № 2
Найти
предел
![]() .
.
Решение.
Имеем неопределённость
вида
![]() .
.
Функции
![]() и
и
![]() дифференцируемы в некоторой окрестности
точки
дифференцируемы в некоторой окрестности
точки
![]() ,
причём
,
причём
![]() .
Воспользуемся правилом Лопиталя:
.
Воспользуемся правилом Лопиталя:
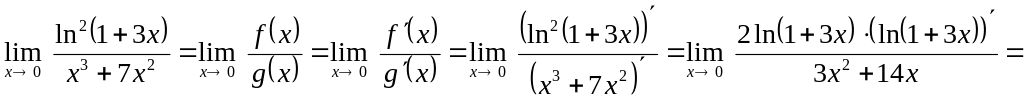
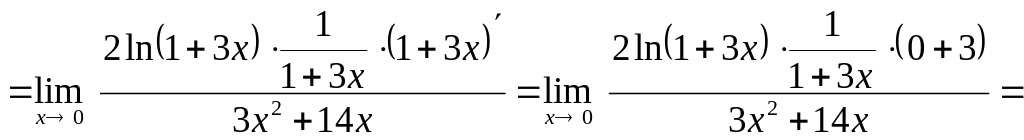
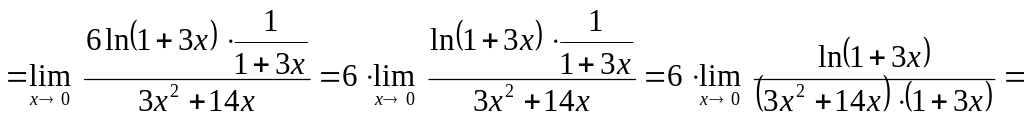

![]()
Снова воспользуемся правилом Лопиталя:
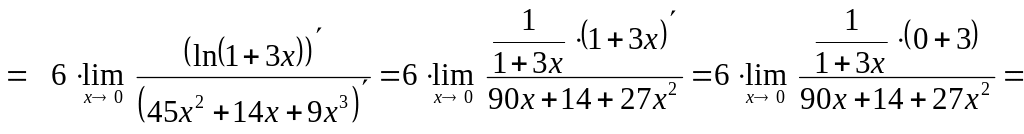

![]() .
.
Ответ:
![]() .
.
Задача № 3
Найти
производную функции
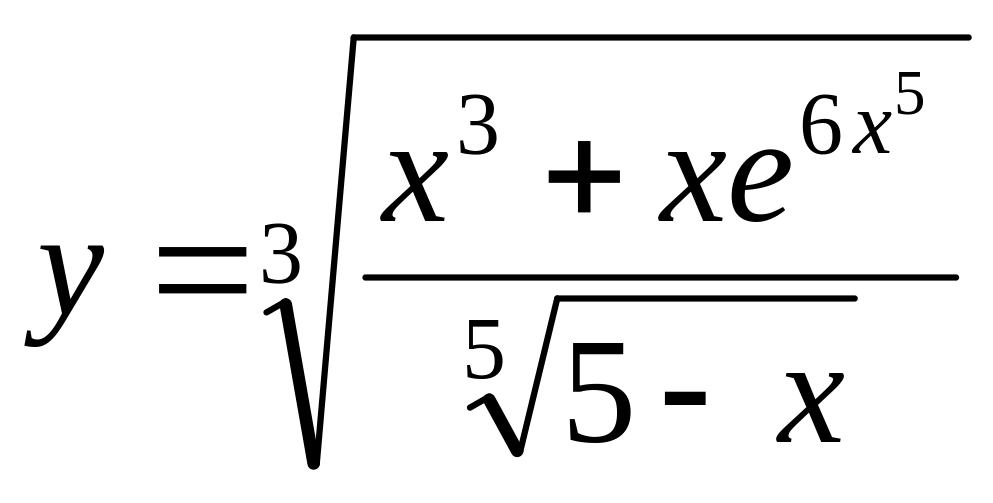 .
.
Решение.
Воспользуемся свойствами производной:
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
где
,
где
![]() – константа, а также таблицей
– константа, а также таблицей
производных:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где С – константа.
,
где С – константа.

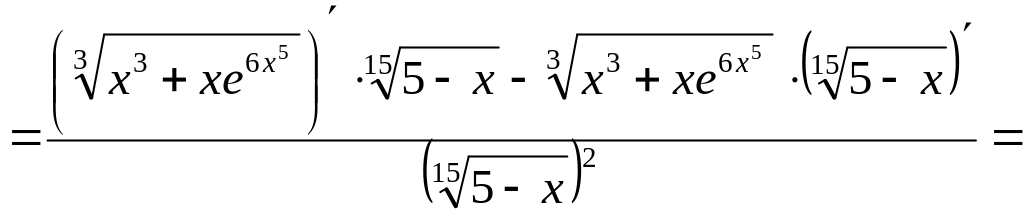
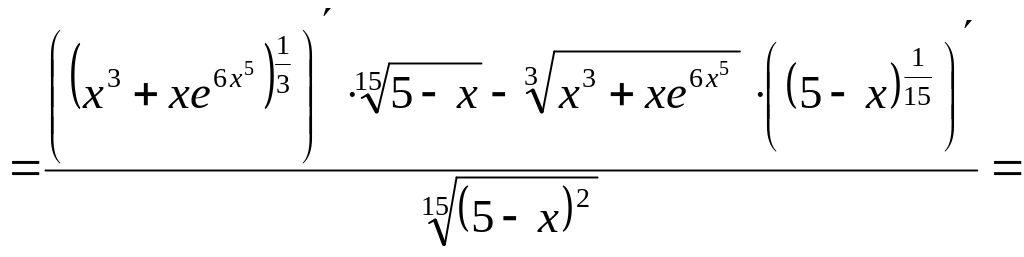
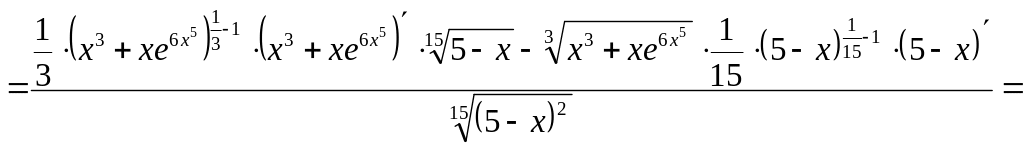
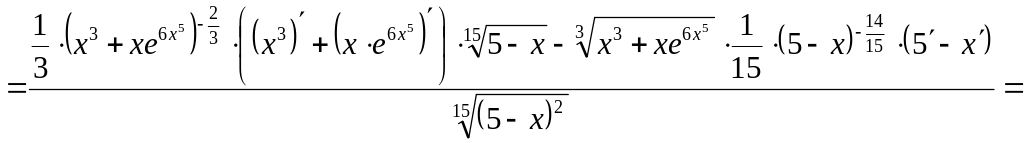
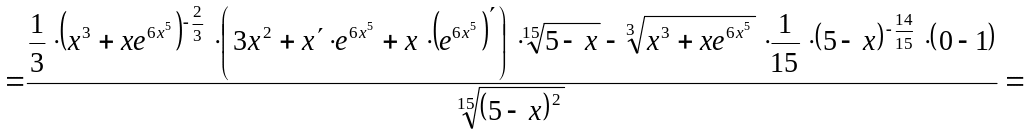
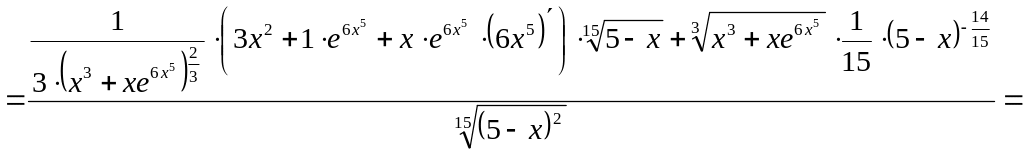
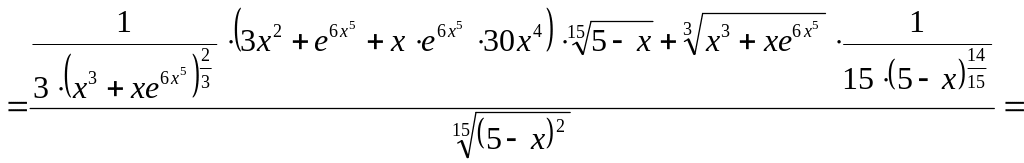
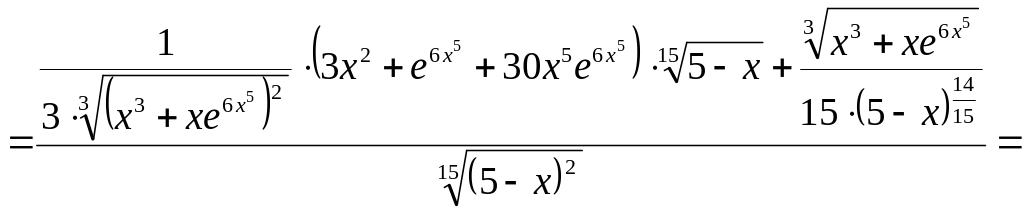
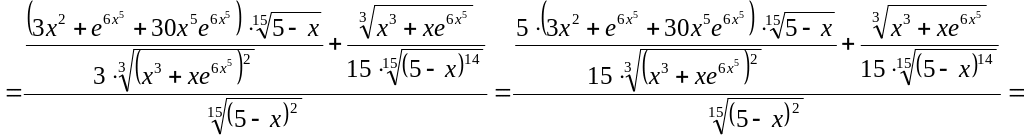
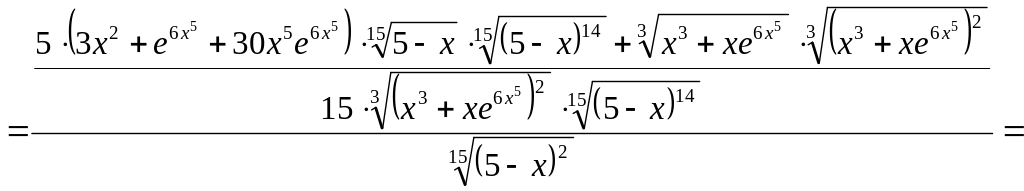
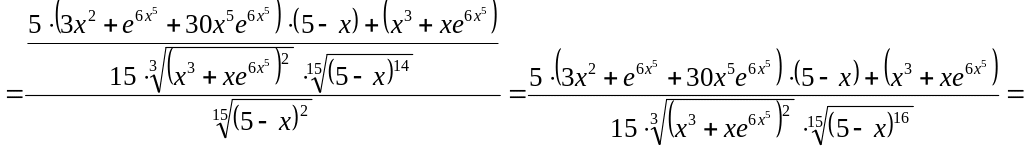
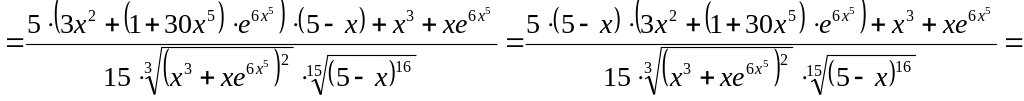
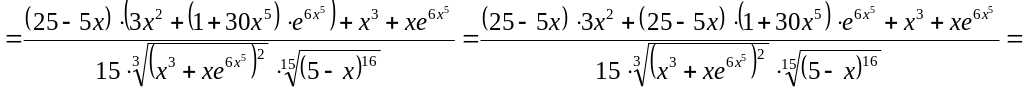
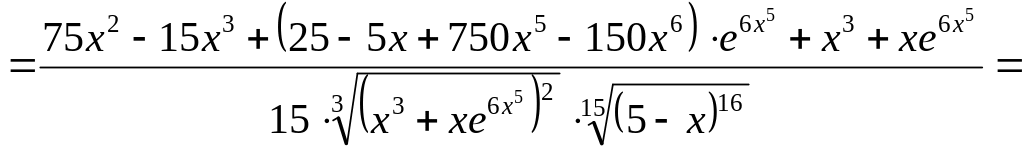
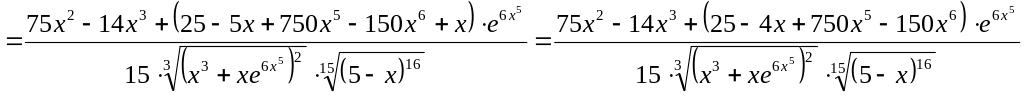 .
.
Ответ:
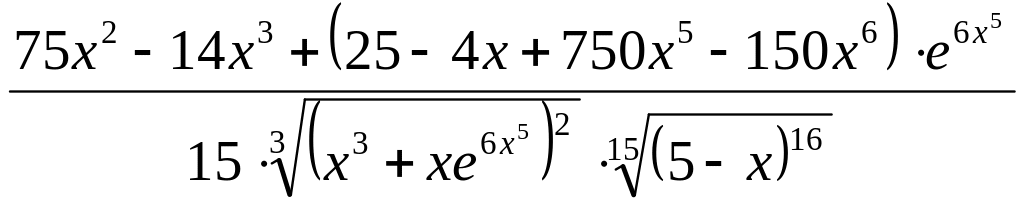 .
.
Задача № 4
Требуется изготовить открытый цилиндрический бак ёмкостью 1000 см3. При каком радиусе основания на изготовление бака уйдёт наименьшее количество материала?
Решение.
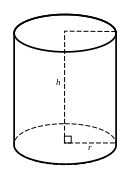
Обозначим:
![]() – радиус основания цилиндра (бака),
– радиус основания цилиндра (бака),
![]() – высоту цилиндра (бака).
– высоту цилиндра (бака).
Объём
бака
![]() .
.
По
условию
![]() (см3), откуда
(см3), откуда
![]() ;
;
![]() .
.
Боковая поверхность бака (цилиндра)
![]() (см2).
(см2).
Площадь
основания цилиндра (дна бака)
![]() (см2).
(см2).
Следовательно,
площадь поверхности бака
![]() .
.
Область
определения функции
![]() :
:
![]() .
.
Исследуем на
экстремум функцию
![]() площади поверхности бака.
площади поверхности бака.
Определим точки возможного экстремума,
то есть точки из
![]() ,
в которых производная
,
в которых производная
![]() либо не существует.
либо не существует.
![]()
![]() .
.
![]() существует при всех
существует при всех
![]() ,
то есть при
,
то есть при
![]() .
.
при
![]() ,
то есть при
,
то есть при
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
Значит
.
Значит
![]() – единственная точка возможного
экстремума, которая разбивает
на два интервала:
– единственная точка возможного
экстремума, которая разбивает
на два интервала:
![]() и
и
![]() .
.
Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:
-


–
0
+
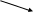
Функция
убывает при
![]() и возрастает при
и возрастает при
![]() .
.
При переходе через точку меняет знак, значит функция имеет экстремум в точке .
При переходе через точку меняет знак с «–» на «+», значит является точкой минимума функции.
![]() ,
,
 (см2).
(см2).
Таким образом, наименьшую площадь
поверхности (наименьшее количество
материала)
![]() (см2) имеет бак, радиус основания
которого
(см2) имеет бак, радиус основания
которого
![]() (см).
(см).
Ответ: чтобы на изготовление
открытого цилиндрического бака ёмкостью
1000 см3 ушло наименьшее количество
материала, радиус основания этого бака
должен быть
![]() (см).
(см).
Задача № 5
Составить уравнения касательных к
графику функции y=(2x+5)/(x+2)
![]() ,
перпендикулярных прямой, проходящей
через точки (0;3) и (1;7)
,
перпендикулярных прямой, проходящей
через точки (0;3) и (1;7)
![]() и
и
![]() .
Сделать чертёж.
.
Сделать чертёж.
Решение.
Уравнение прямой, проходящей через две
заданные точки плоскости
![]() и
и
![]() имеет вид:
имеет вид:
![]() .
.
Воспользовавшись этой формулой, найдём
уравнение прямой, проходящей через
точки
![]() и
и
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() – уравнение прямой, проходящей через
точки
и
.
– уравнение прямой, проходящей через
точки
и
.
Угловой коэффициент
![]() прямой
прямой
![]() найдём, записав полученное уравнение
в виде
найдём, записав полученное уравнение
в виде
![]() уравнения прямой с заданным угловым
коэффициентом:
уравнения прямой с заданным угловым
коэффициентом:
![]() ,
откуда
,
откуда
![]() .
.
Воспользуемся условием
![]() перпендикулярности двух прямых,
заданных уравнениями
перпендикулярности двух прямых,
заданных уравнениями
![]() и
и
![]() .
.
Пусть
![]() – угловой коэффициент искомых
касательных к кривой
.
– угловой коэффициент искомых
касательных к кривой
.
Поскольку искомые касательные к
гиперболе
перпендикулярны прямой
,
получаем:
![]() .
.
Итак, угловой коэффициент искомых
касательных
![]() .
.
С другой стороны, угловой коэффициент
искомых касательных к гиперболе
в точке
![]() равен
равен
![]() .
.
Найдём
![]() :
:
![]() ;
;
![]() .
.
Таким образом,
и
![]() ,
откуда
,
откуда
![]() ;
;
![]() ;
;
![]() ;
;
![]() или
или
![]() ;
;
![]()
![]() .
.
Соответственно при
получаем:
![]() ;
;
![]() ,
,
а при
получаем:
![]() ;
.
;
.
Значит искомые касательные – это
касательные графику функции
в точках
![]() и
и
![]() .
.
Уравнение касательной к кривой
![]() в точке
в точке
![]() имеет вид
имеет вид
![]() .
.
Уравнение касательной к гиперболе в точке имеет вид:
![]() ;
;
![]() ;
;
![]() .
.
Уравнение касательной к гиперболе в точке имеет вид:
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, касательные, проведённые к графику функции , перпендикулярные прямой, проходящей через точки и , имеют уравнения и .

|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
-6 |
|
-4 |
|
-2 |
|
О |
|
2 |
|
4 |
|
6 |
|
8 |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
![]() и
.
и
.
