- •III осенний семестр Лекция №1 Числовые ряды
- •Лекция №2 Сходимость положительных рядов
- •Лекция №3 Сходимость положительных рядов (продолжение)
- •Лекция №4 Сходимость положительных рядов (продолжение)
- •Ряды с членами произвольного знака
- •Лекция №5 Ряды вида
- •Лекция №6 Перестановки числовых рядов
- •Лекция №6 Перестановки числовых рядов (продолжение)
- •Лекция №8 Умножение рядов (продолжение)
- •Двойные ряды
- •Лекция №9 Двойные ряды (продолжение)
- •Бесконечные произведения
- •Лекция №10 Бесконечные произведения (продолжение)
- •Лекция №11 Функции, представляющиеся в виде бесконечных произведений
- •Функциональные последовательности и ряды
- •Лекция №12 Функциональные последовательности и ряды (продолжение)
- •Лекция №13 Функциональные последовательности и ряды (продолжение)
- •Лекция №14 Свойства предельной функции и сумма функционального ряда в случае равномерной сходимости
- •Лекция №15 Пространства и сходимость в них
- •Степенные ряды
- •Лекция №16 Степенные ряды (продолжение)
- •Лекция №17 Разложение функций в степенные ряды
- •Лекция №18 Ряды Фурье
- •Лекция №19 Ряды Фурье (продолжение)
- •Лекция №20-21 Ряды Фурье (продолжение)
- •Лекция №22 Ряды Фурье (продолжение)
- •Лекция №23 Ряды Фурье (продолжение)
- •Лекция №24 Ряды Фурье (продолжение)
- •Лекция №25 Ряды Фурье (продолжение).
- •Лекция №26 Поточечная сходимость тригонометрического ряда Фурье
- •Лекция №27 Поточечная сходимость тригонометрического ряда Фурье (продолжение)
- •Лекция №28 Собственные интегралы, зависящие от параметра
- •Несобственные интегралы, зависящие от параметра
- •Лекция №29 Несобственные интегралы, зависящие от параметра (продолжение)
- •Лекция №30 Свойства несобственных интегралов, зависящих от параметра
- •Свойства гамма-функции
- •Лекция№31 Преобразование Фурье
- •Разложение в ряд Тейлора-Маклорена некоторых элементарных функций
Лекция №23 Ряды Фурье (продолжение)
Исследуем достаточные условия сходимости тригонометрического ряда Фурье. Для этого определим следующий класс функций.
2-периодическую
функцию
![]() назовём
кусочно-непрерывно-дифференцируемой,
если тор, или период, можно разбить на
конечное число дуг или отрезков, на
каждой из которых функция является
непрерывно дифференцируемой.
назовём
кусочно-непрерывно-дифференцируемой,
если тор, или период, можно разбить на
конечное число дуг или отрезков, на
каждой из которых функция является
непрерывно дифференцируемой.
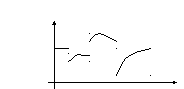

Функция называется кусочно-непрерывно-дифференцируемая, если она кусочно-непрерывно-дифференцируемая и непрерывна на всём периоде.
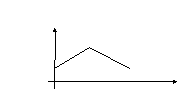
непрерывная кусочно-дифференцируемая функция
Теорема. Тригонометрический ряд Фурье непрерывной кусочно-непрерывной дифференцируемой функции сходится к ней равномерно.
Доказательство.
Для простоты
рассмотрим случай
![]()
В ыразим
коэффициенты Фурье функцииf
через коэффициенты её производной, и
для доказательства равномерной сходимости
воспользуемся признаком Вейерштрасса.
Т.к. из равномерной сходимости вытекает
среднеквадратичная, а тригонометрический
ряд Фурье в среднеквадратичном сходится
именно к функции, то он будет равномерно
сходится к этой функции.
ыразим
коэффициенты Фурье функцииf
через коэффициенты её производной, и
для доказательства равномерной сходимости
воспользуемся признаком Вейерштрасса.
Т.к. из равномерной сходимости вытекает
среднеквадратичная, а тригонометрический
ряд Фурье в среднеквадратичном сходится
именно к функции, то он будет равномерно
сходится к этой функции.
Имеем:
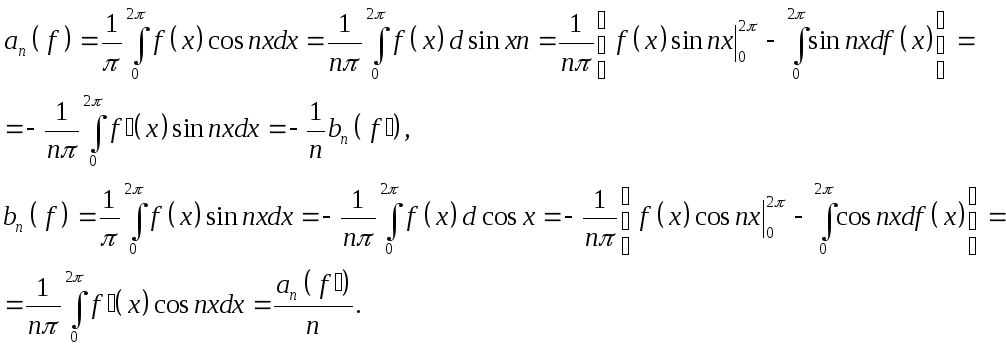
Итак,
![]()
Далее
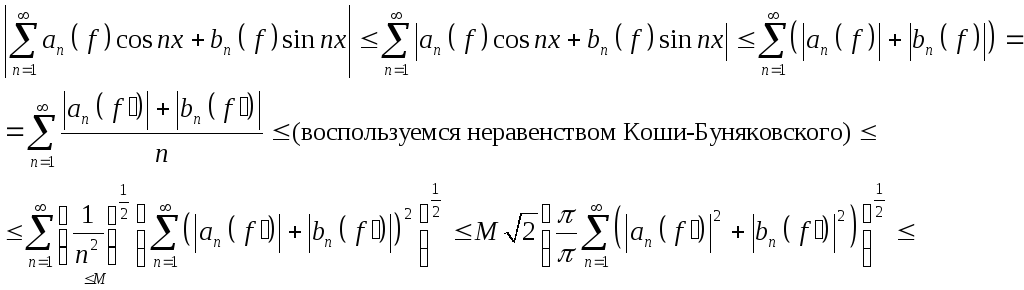
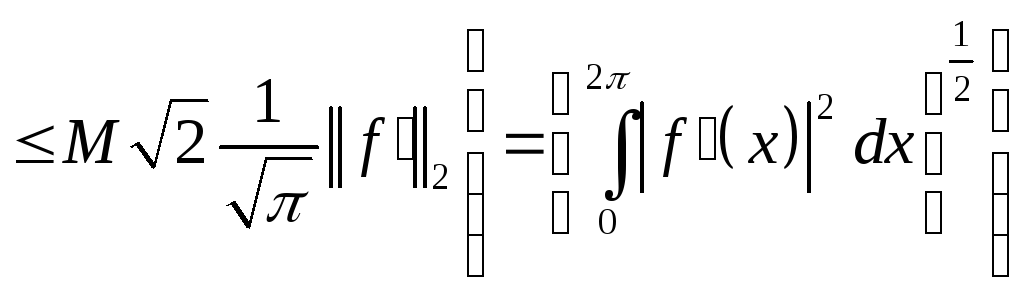 и
по признаку Вейерштрасса тригонометрический
ряд Фурье сходится равномерно.
и
по признаку Вейерштрасса тригонометрический
ряд Фурье сходится равномерно.
Доказано.
Построим суммы к бесконечным частичным суммам ряда Фурье, но обладающие свойством равномерной сходимости для произвольной непрерывной функции. Определим эти суммы следующим образом:
![]() суммы
Фейера (по
имени Л. Фейера), являющиеся тригонометрическим
полиномом порядка п,
в интегральном представлении которых
участвует ядро, называемое ядром
Фейера.
суммы
Фейера (по
имени Л. Фейера), являющиеся тригонометрическим
полиномом порядка п,
в интегральном представлении которых
участвует ядро, называемое ядром
Фейера.
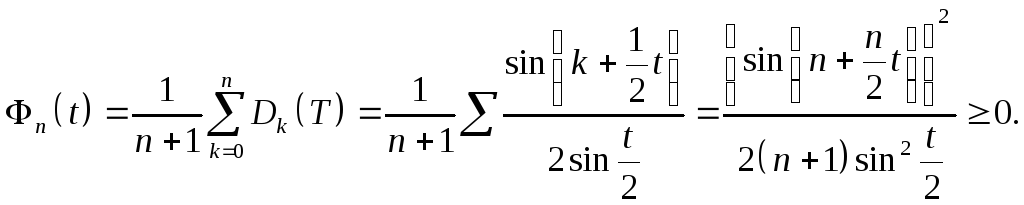
Другая запись ряда Фейера имеет вид:

разрыв
Пример 1. Ряд
![]() расходится,
расходится,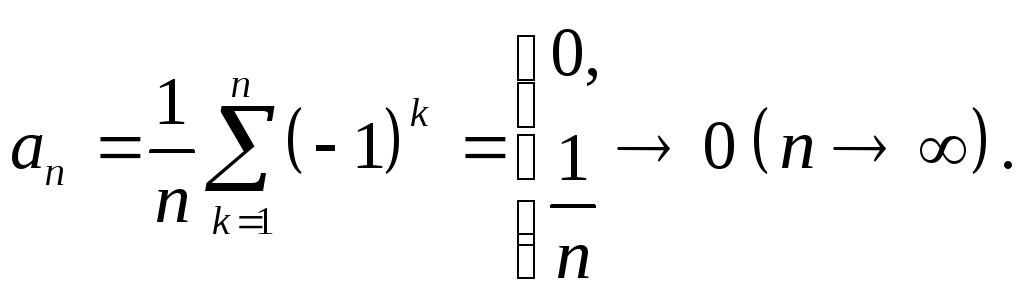
Пример 2.
![]() «скорость»
приближения функции.
«скорость»
приближения функции.
Лекция №24 Ряды Фурье (продолжение)
Проверим, что для сумм Фейера выполнены оба условия в теореме Банаха-Штейнгауза. Это будет означать, что сумма Фейера равномерно сходится к любой непрерывной функции. Имеем:
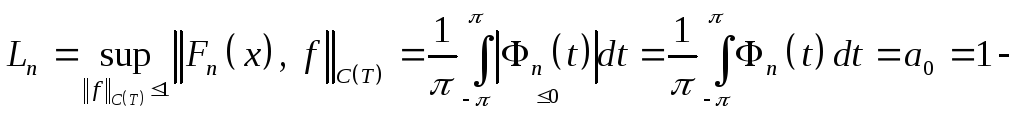 ограничены;
ограничены;сходимость на плотном множестве тригонометрических полиномов. Достаточно проверить сходимость
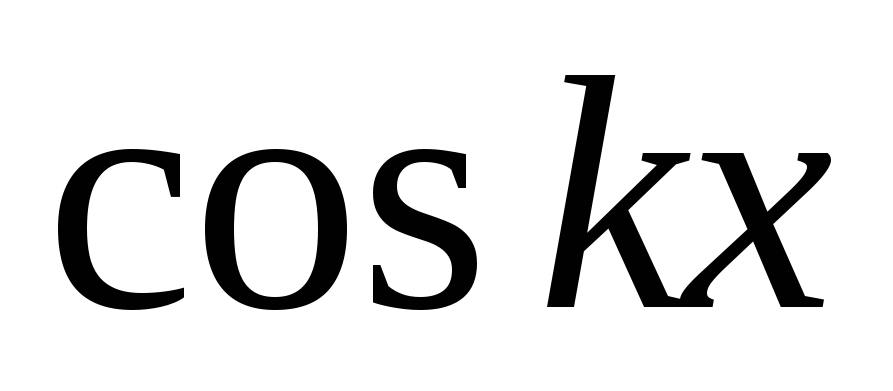 и
и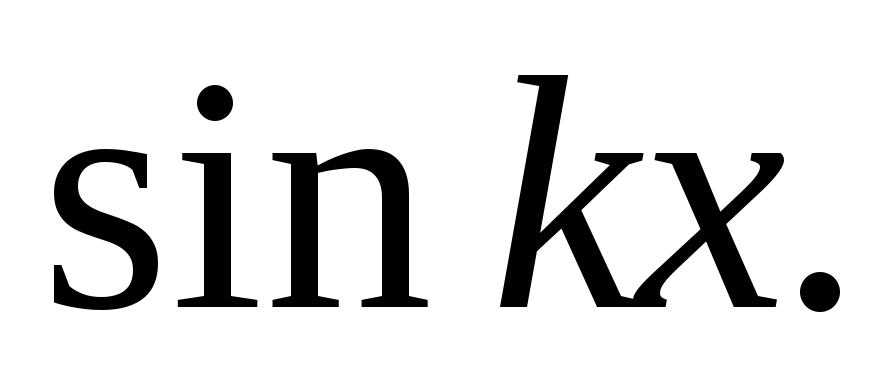
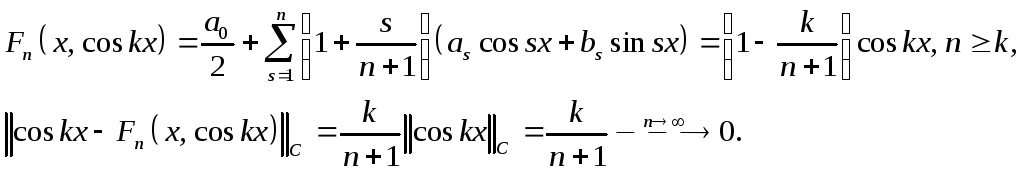
Аналогично
доказывается равномерная сходимость
для
![]()
Предложим и другие доказательство равномерной сходимости сумм Фейера.
Теорема.
![]()
Доказательство. Имеем:

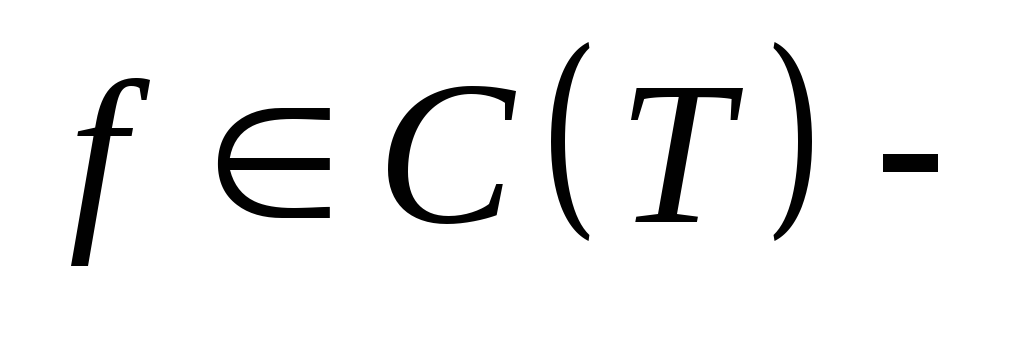 равномерно
непрерывна и ограничена, т.е.
равномерно
непрерывна и ограничена, т.е.
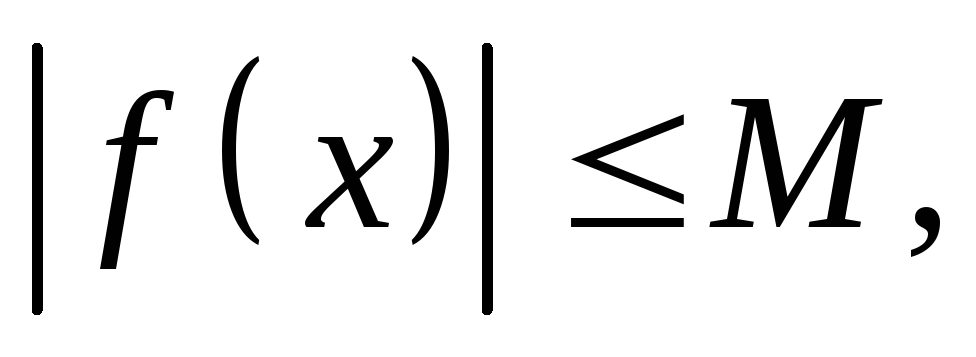 Т
– тор, компактное множество.
Т
– тор, компактное множество.
Имеем:
![]()
![]()
![]()
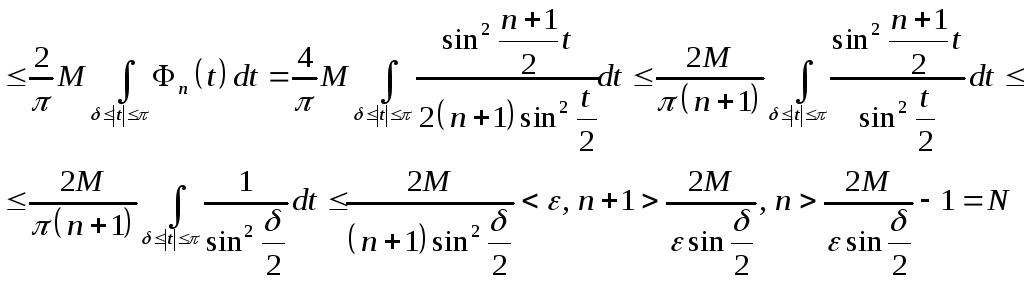
и для этих п
будет
![]()
Окончательно,
![]()
Доказано.
Следствием этой теоремы является теорема Вейерштрасса о возможности равномерного приближения любой непрерывной периодической функции тригонометрическими полиномами. Эта теорема была сформулирована при доказательстве замкнутости в среднеквадратичном тригонометрической системы.
В качестве следствия из этой теоремы можно получить и другую теорему Вейерштрасса.
Теорема
Вейерштрасса.
Множество алгебраических многочленов
плотно в пространстве
![]() Это
означает, что
Это
означает, что![]() некоторой
степени, такой, что
некоторой
степени, такой, что![]()
Лекция №25 Ряды Фурье (продолжение).
Теорема Вейерштрасса-Стоуна
Пусть
![]() компактное
множество,
компактное
множество,![]() множество
всех непрерывных функций наК,
множество
всех непрерывных функций наК,
![]() непрерывна,
если
непрерывна,
если![]()
Пространство
![]() являетсяполным
линейным нормированным пространством
с нормой
являетсяполным
линейным нормированным пространством
с нормой
![]()
Множество
![]() назовём
плотным в
назовём
плотным в![]() если
если![]()
![]()
Подмножество
![]() назовёмалгеброй,
если
назовёмалгеброй,
если
![]() будет:
будет:
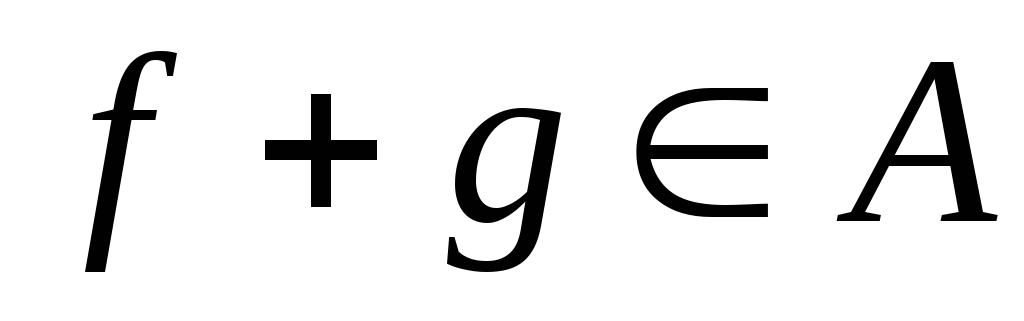 (замкнуто
относительно суммы);
(замкнуто
относительно суммы);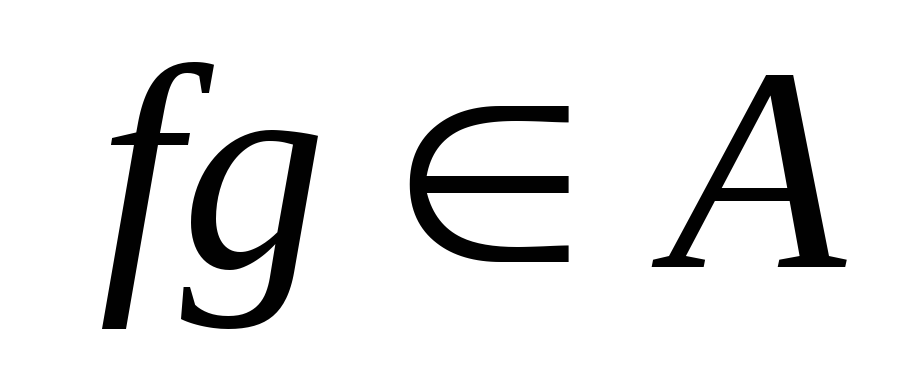 (замкнуто
относительно произведения);
(замкнуто
относительно произведения);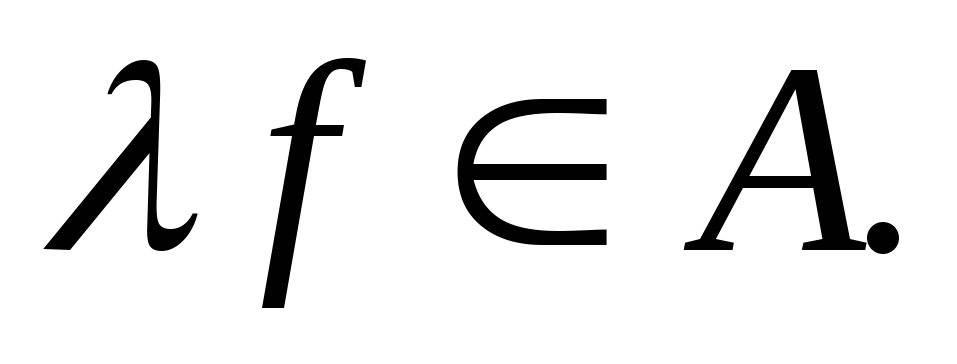
Примерами алгебр являются множества всех алгебраических многочленов Р, множество всех тригонометрических полиномов M.
Будем говорить,
что алгебра А
разделяет точки компакта К,
если
![]() АлгебрыР
и M
разделяют точки своих компактов.
АлгебрыР
и M
разделяют точки своих компактов.
Будем говорить,
что алгебра не исчезает ни в одной точке
компакта К,
если
![]() АлгебрыР
и M
не исчезают ни в одной точке.
АлгебрыР
и M
не исчезают ни в одной точке.
Теорема
Вейерштрасса-Стоуна. Любая
алгебра
![]() разделяющая
точки компактаК
и не исчезающая ни в одной точке компакта
К,
образует плотное множество в
разделяющая
точки компактаК
и не исчезающая ни в одной точке компакта
К,
образует плотное множество в
![]()
Примем без доказательства.
По аналогии с
многочленами от одной переменной можно
определить многочлены от п
переменных как конечные линейные
комбинации функций вида
![]() Такая
функция называетсямамоном.
Мамон является многочленом степени
Такая
функция называетсямамоном.
Мамон является многочленом степени
![]() Степенью
произвольного многочлена называют
наибольшую степень мамона, входящую в
этот многочлен.
Степенью
произвольного многочлена называют
наибольшую степень мамона, входящую в
этот многочлен.
Пример. Степень
многочлена
![]() равна
3, т.е. это мамон 3-ей степени.
равна
3, т.е. это мамон 3-ей степени.
Показать
самостоятельно, что эта алгебра разделяет
точки произвольного компакта
![]() и
не исчезает ни в одной точке компактаК.
Поэтому из теоремы Вейерштрасса-Стоуна
сразу получаем, что
и
не исчезает ни в одной точке компактаК.
Поэтому из теоремы Вейерштрасса-Стоуна
сразу получаем, что
![]() плотно
в
плотно
в![]()
Задача. Пусть
![]() Показать,
чтоА
– алгебра и найти необходимое и
достаточное условие, чтобы эта алгебра
разделяла точки отрезка
Показать,
чтоА
– алгебра и найти необходимое и
достаточное условие, чтобы эта алгебра
разделяла точки отрезка
![]() и
не исчезала ни в одной точке
и
не исчезала ни в одной точке![]() т.е.
была бы плотна в пространстве
т.е.
была бы плотна в пространстве![]()
Алгебра А
разделят точки тогда и только тогда,
когда функция строго монотонна на
![]() Действительно,
если
Действительно,
если![]() например,
строго возрастающая, то
например,
строго возрастающая, то![]()
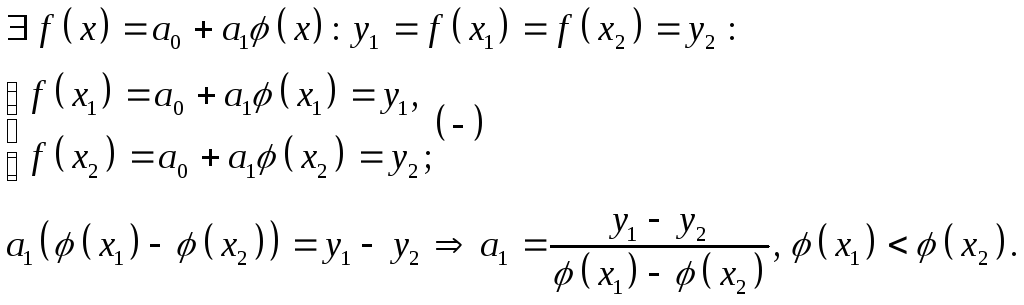
Следовательно,
![]()
Если
![]() не
является строго монотонной, то
не
является строго монотонной, то![]() в
которых функция принимает одинаковые
значения. Тогда
в
которых функция принимает одинаковые
значения. Тогда![]() и
точки
и
точки![]() и
и![]() не
разделяются.
не
разделяются.
Убедимся на примерах, что в теореме Вейерштрасса-Стоуна оба дополнительных условия являются важными.
Пример 1. Укажем
алгебру в пространстве
![]() не
разделяющую точки и не плотную в
не
разделяющую точки и не плотную в![]() Такая
алгебра может быть выбрана как подалгебраР.
Тривиальный пример – константы. Менее
тривиальный пример – множество всех
чётных многочленов
Такая
алгебра может быть выбрана как подалгебраР.
Тривиальный пример – константы. Менее
тривиальный пример – множество всех
чётных многочленов
![]() Это
множество не является плотным в
пространстве
Это
множество не является плотным в
пространстве![]()
Пример 2. Укажем
алгебру (подалгебру) многочленов на
![]() исчезающую
в некоторой точке. В качестве такой
алгебры можно взять множество всех
нечётных многочленов
исчезающую
в некоторой точке. В качестве такой
алгебры можно взять множество всех
нечётных многочленов
![]() Все
эти функции исчезают в нуле, и эти функции
не приближают
Все
эти функции исчезают в нуле, и эти функции
не приближают
![]() т.к.
т.к.![]()