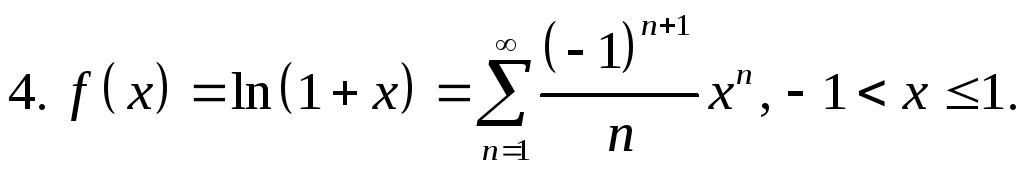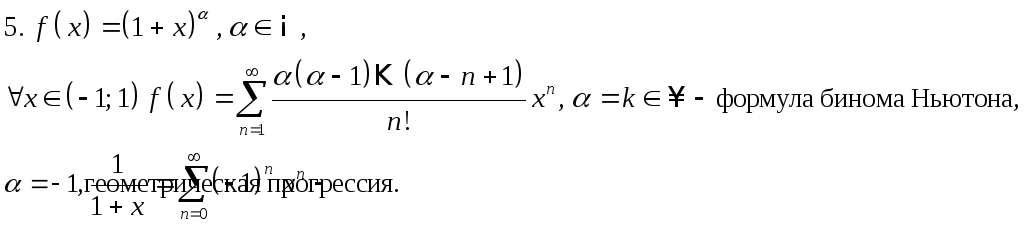Степенные ряды

1. Определение степенного ряда

Степенным рядом называется ряд вида коэффициенты степенного ряда,

Нашей основной задачей будет исследование области поточечной сходимости, равномерной сходимости и свойств суммы (1).

Положительное число называетсярадиусом сходимости ряда (1), если при ряд (1) сходится, а приЧислоназывается интервалом сходимости.

Теорема 1(об области поточечной сходимости). Любой ряд вида (1) имеет радиус сходимости 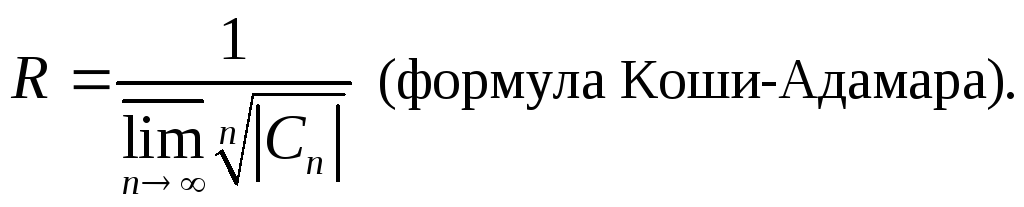Точнее:

1. если 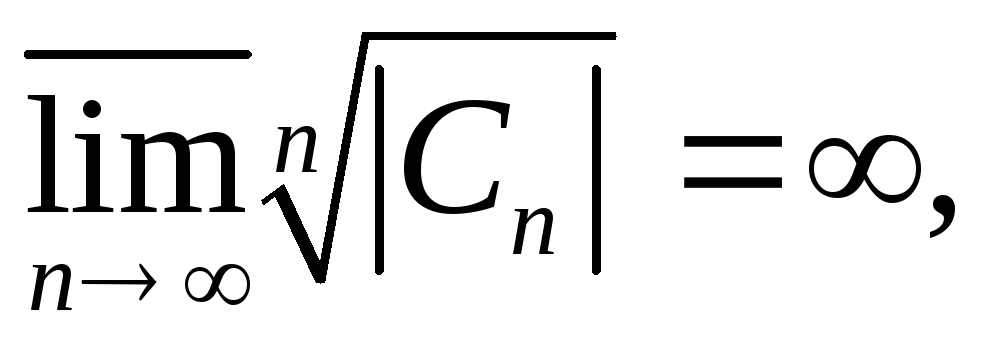то область сходимости

2. если

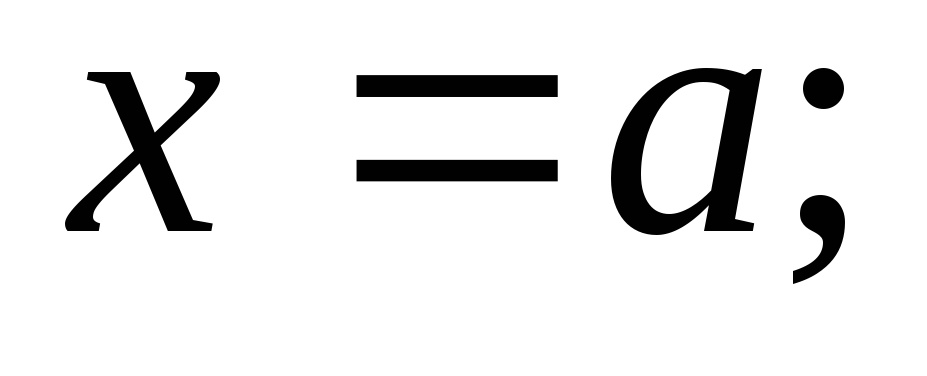
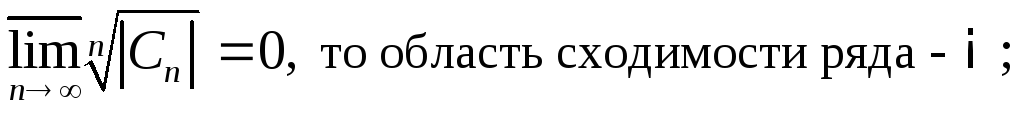
3. есл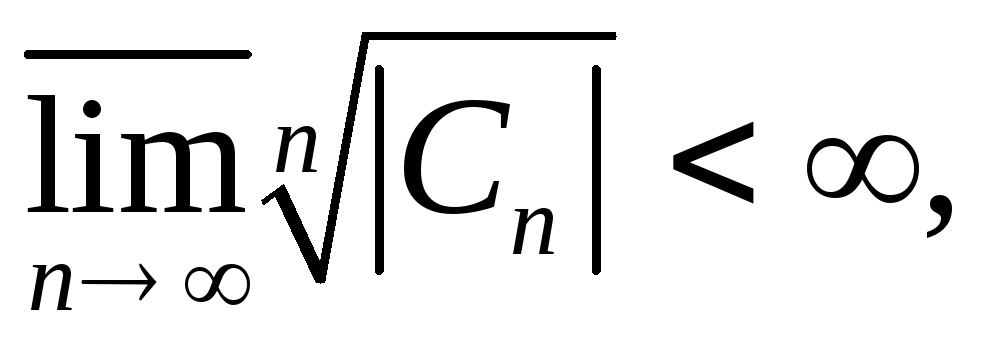и то при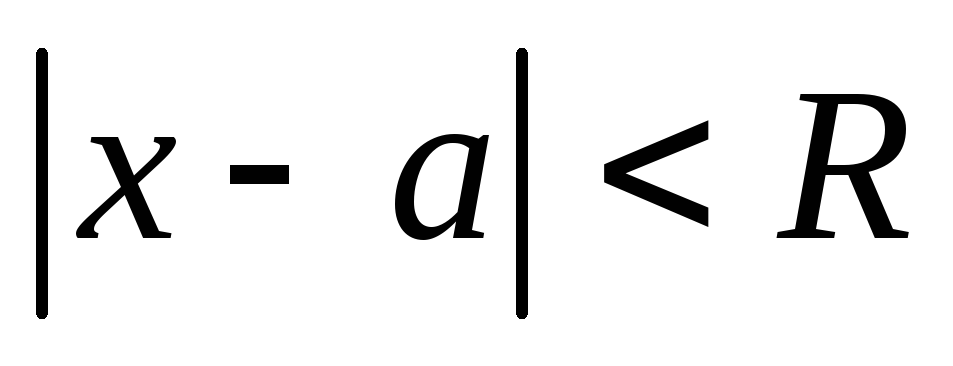ряд (1) сходится, а при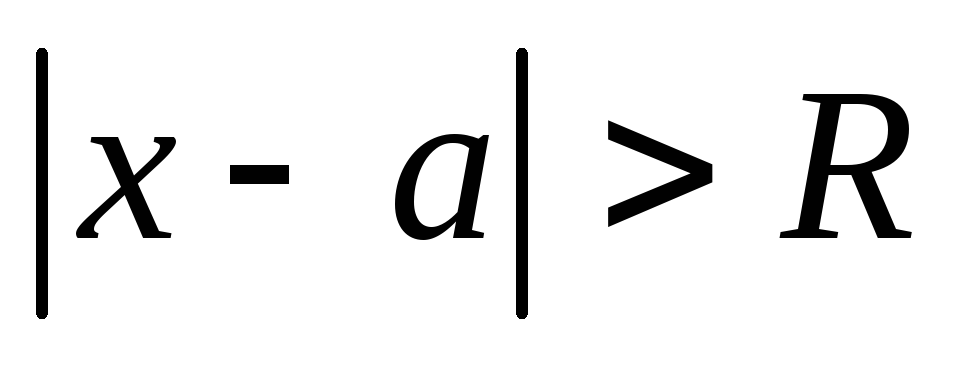ряд (1) - расходится, причём в интервале сходимости ряд (1) будет сходиться абсолютно.

Доказательство. При доказательстве будем использовать радикальный признак Коши в следующей форме:

1. если 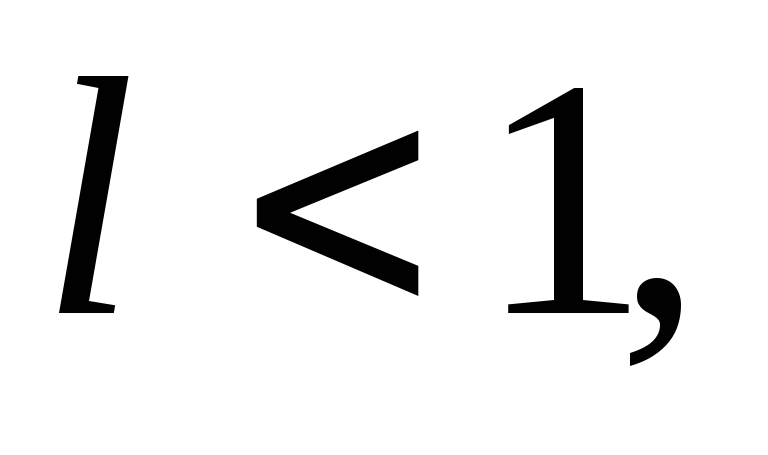то ряд (2) сходится;

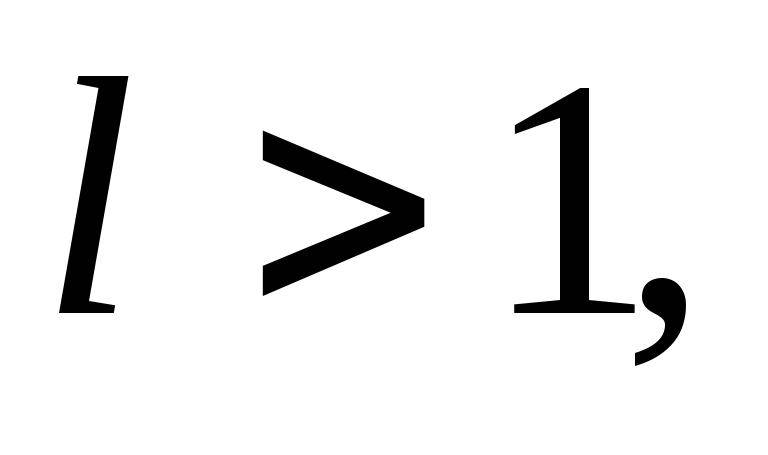2. если то ряд (2) расходится и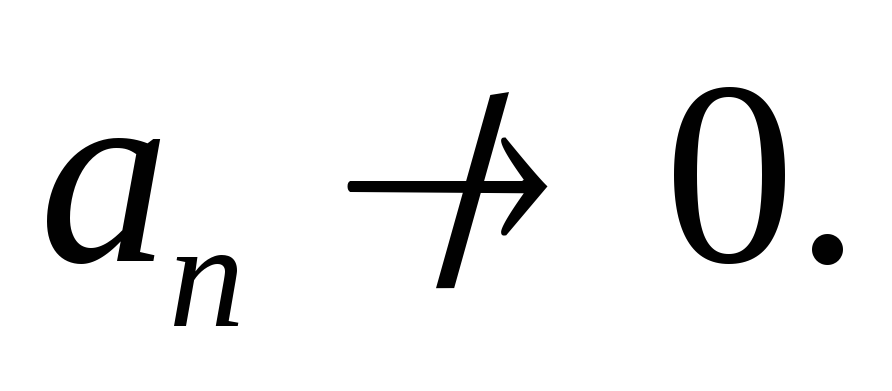

Исследуем абсолютную сходимость ряда (1):

1. 

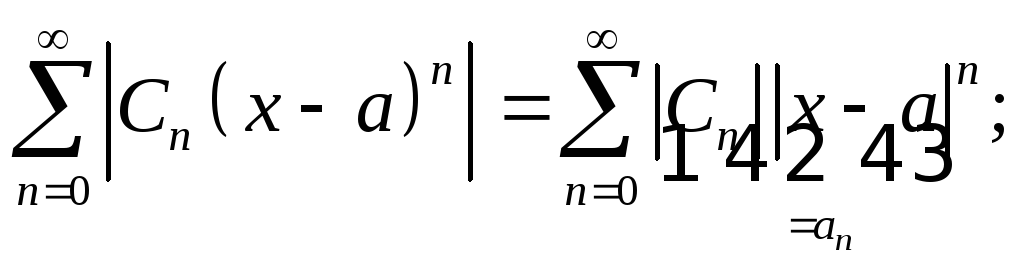
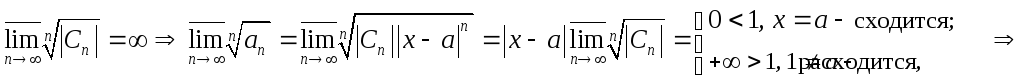
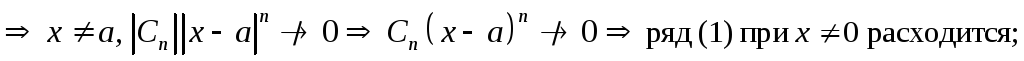
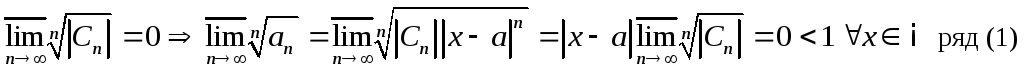2. сходится абсолютно.

Доказано.

Пример. Исследовать сходимость ряда

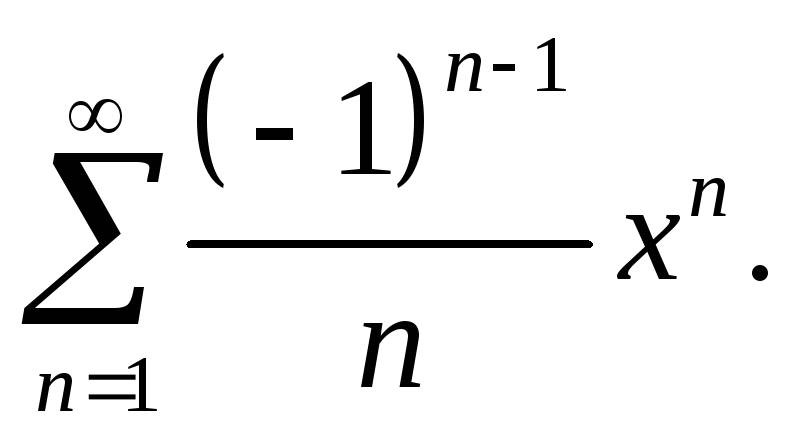
Исследуем абсолютную сходимость ряда.

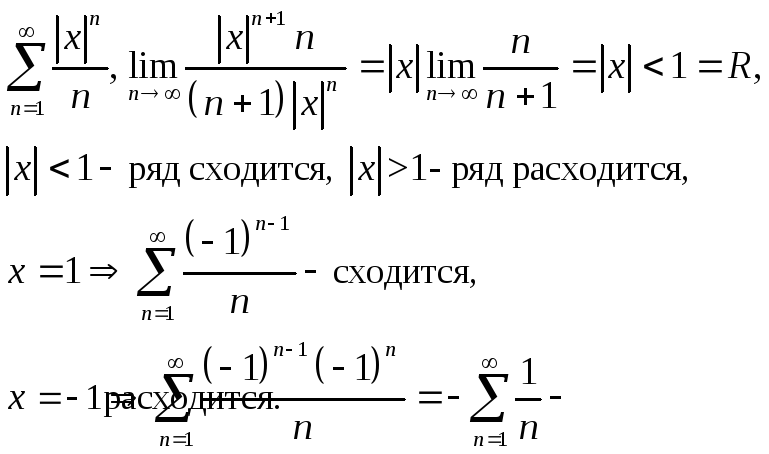
Итак, область абсолютной сходимости - область сходимости ряда -

Лекция №16 Степенные ряды (продолжение)

Теорема 2 (область равномерной сходимости). Степенной ряд (1) сходится равномерно на любом отрезке, лежащим в интервале сходимостиЕсли ряд (1) сходится пригдеЕсли ряд (1) сходится прито он сходится равномерно на любом отрезке вида

Доказательство. Пусть (1) сходится в интервале Покажем, что ряд (1) сходится равномерно на отрезкеТ.к. ряд (1) сходится приабсолютно, то мы можем воспользоваться признаком равномерной сходимости Вейерштрасса.

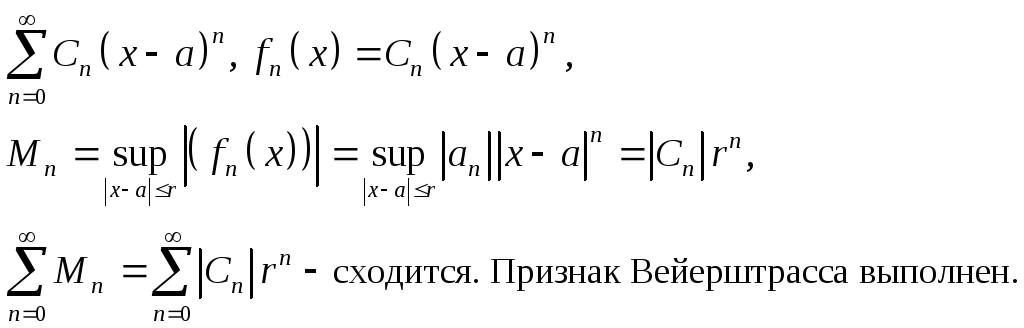
Пусть (1) сходится при Достаточно доказать равномерную сходимость на отрезкеВоспользуемся признаком равномерной сходимости Абеля:

1. 

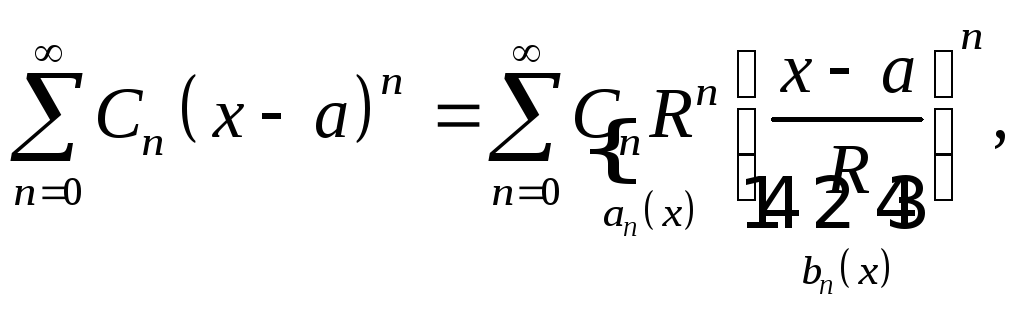
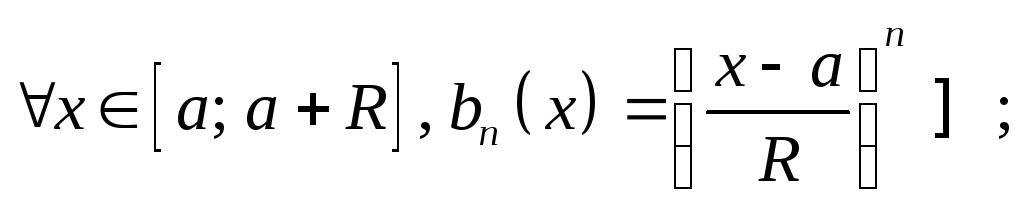
2. равномерная ограниченность

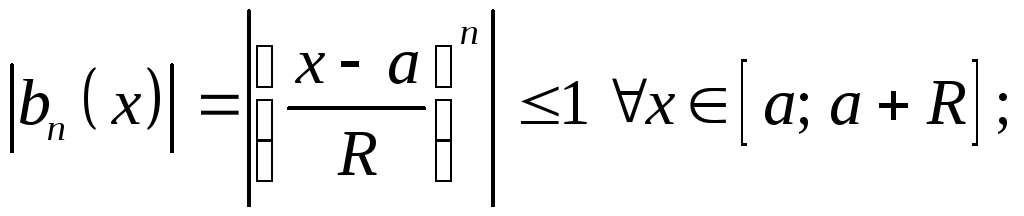
3. ряд

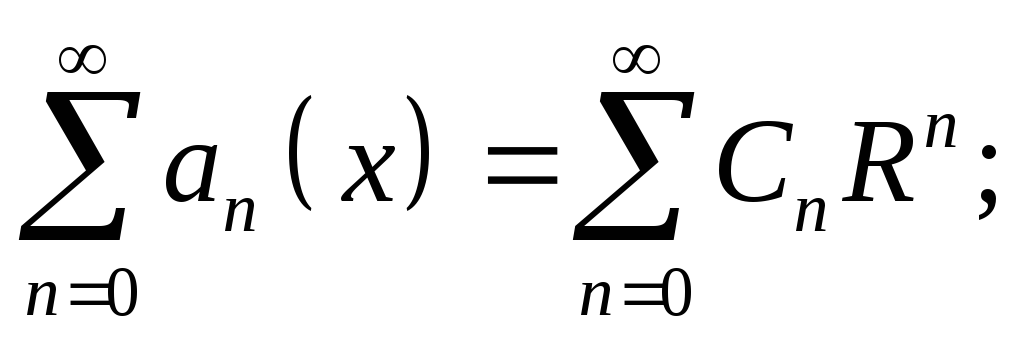
Условия выполнены и значит ряд (1) сходится равномерно на

Доказано.

Теорема 3. Степенной ряд в интервале сходимости является бесконечно дифференцируемой функцией и его можно дифференцировать и интегрировать в интервале сходимости:

Доказательство вытекает из описания области равномерной сходимости степенного ряда, трёх теорем о свойствах суммы функционального ряда и того, что при почленном интегрировании радиус сходимости не меняется: 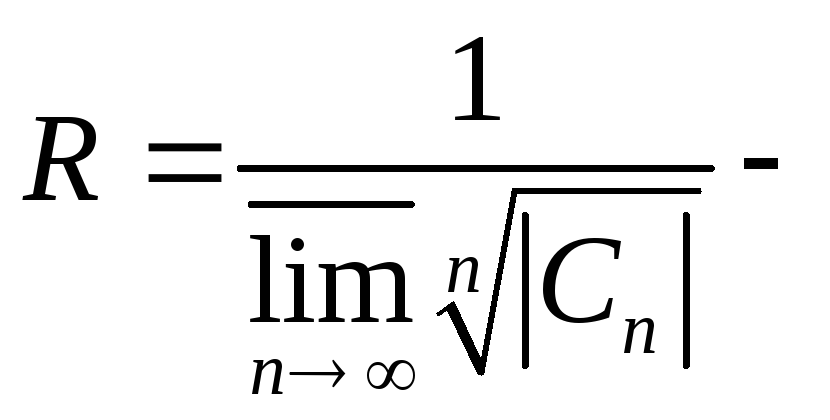радиус сходимости ряда (1).

радиус сходимости продифференцированного ряда (1).

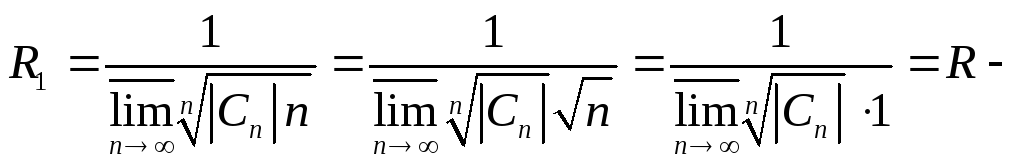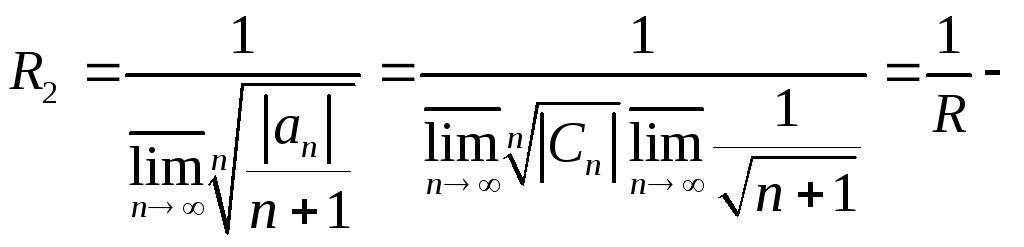радиус сходимости проинтегрированного ряда (1), т.е. радиус сходимости не изменился.

Доказано.

Замечание. Непрерывность суммы степенного ряда можно гарантировать на множестве если в область сходимости входят точкиНапример:

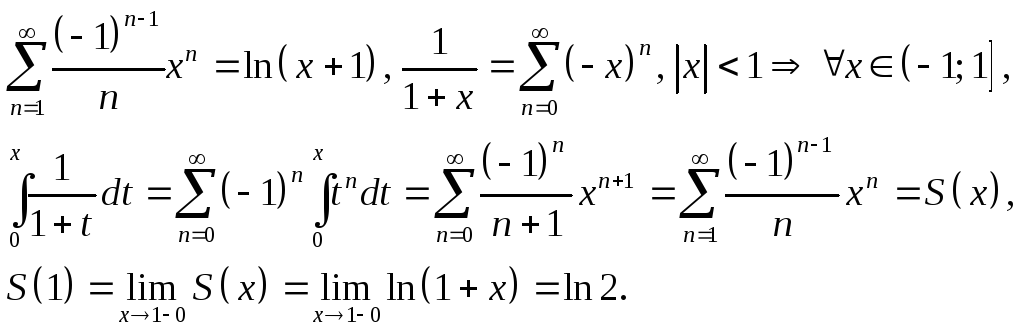
Лекция №17 Разложение функций в степенные ряды

Если функция раскладывается в степенной ряд (1) в некоторой окрестности точки а, то эта функция является бесконечно дифференцируемой в этой окрестности.

Пример.

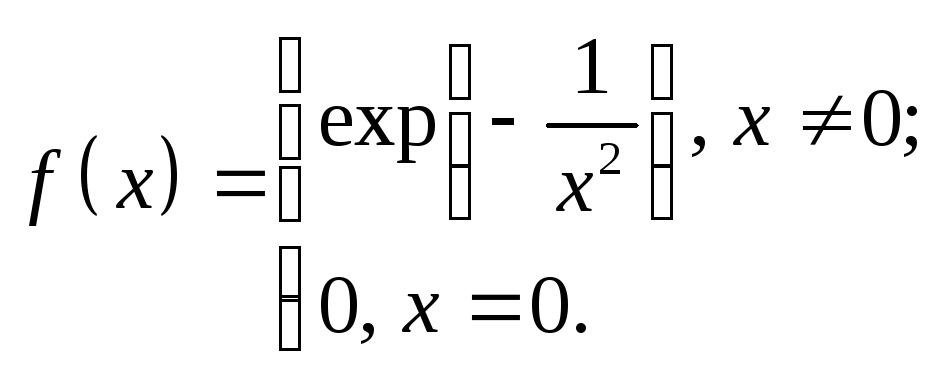
непрерывна и имеет производные любого порядка и при

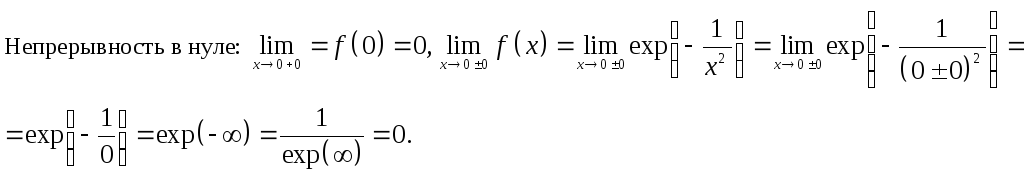
Производная в нуле:

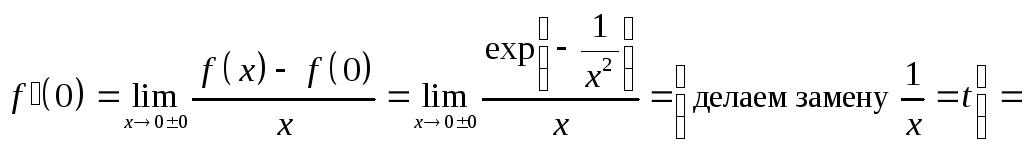
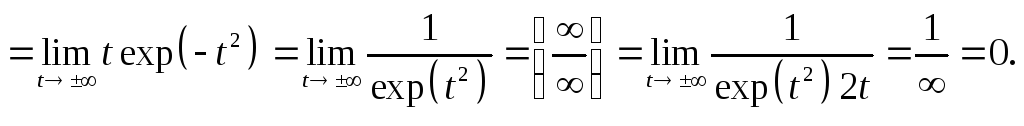
Теорема (о единственности разложения функции в степенной ряд). Если в некоторой окрестности точки а

Степенной ряд вида называетсярядом Тейлора в окрестности точки а. Таким образом, если функция раскладывается в степенной ряд, то он является рядом Тейлора. Например:

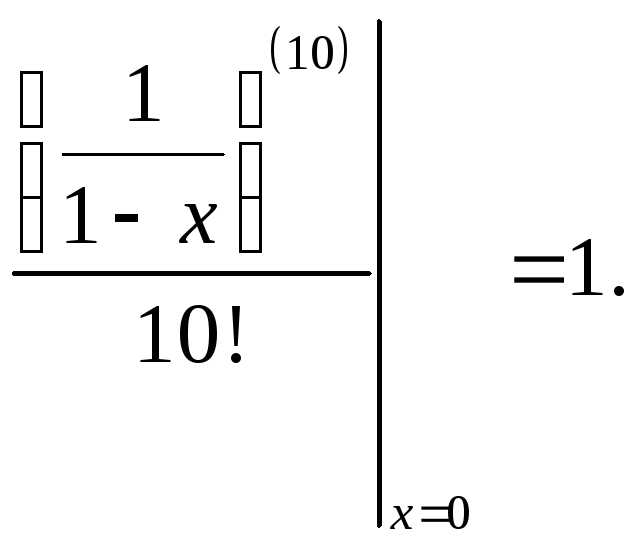
Доказательство.

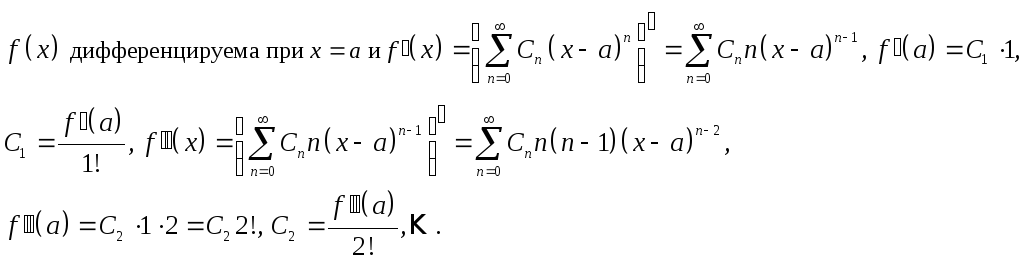
Доказано.

Вернёмся к предыдущему примеру. Если ранее введённая функция раскладывается в степенной ряд в некоторой окрестности точки противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.

Исследуем условия разложимости функции в степенной ряд. Для этого воспользуемся формулой Тейлора:

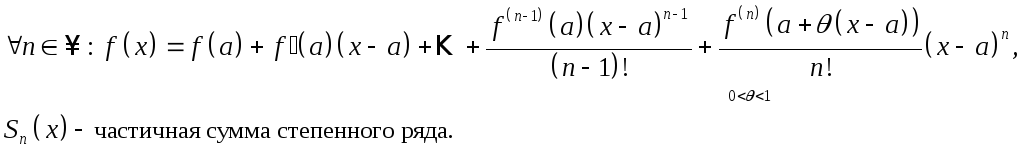
Отсюда, раскладывается в степенной ряд в точкеа тогда и только тогда, когда:

Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд.

Теорема. Если то

.

Доказательство.

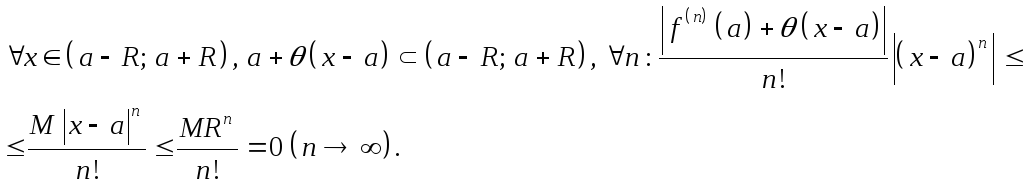
Убедимся, что Удобнее всего для этого рассмотреть ряд и доказать сходимостьПо признаку Даламбера получаем:

ряд сходится, и в таком случае предел общего члена равен нулю.

3. Разложение элементарных функций в ряды Тейлора-Маклорена.

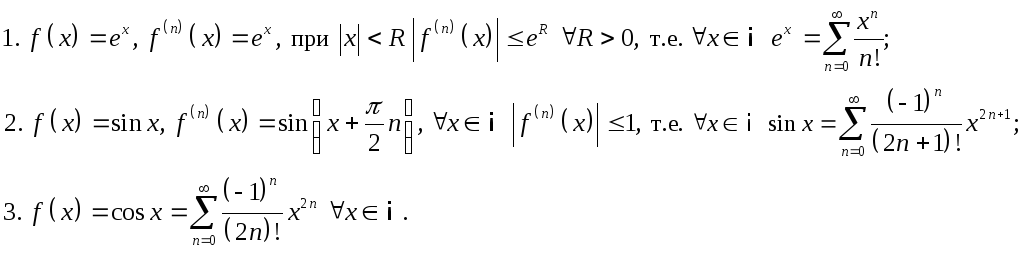
Последнее разложение получено почленным дифференцированием предыдущего разложения.