
Критерий ско
СКО
= ![]()
mi - центр i-ого кластера
wi – iый кластер. Чем меньше СКО, тем более компактны кластеры, тем лучше качество кластеризации, но слишком маленькое тоже не подходит.
Математическое обоснование данного метода заключается в том, что точки, принадлежащие одному кластеру расположены близко друг к другу, а точки принадлежащие другому кластеру далеко. Соответственно, исходя из этого, формирование кластеров будет осуществляться следующим образом. Перебирая все возможные варианты, группируем точки в кластеры и вычисляем СКО для каждого кластера и суммируем их. Затем, отслеживая изменение значения суммарного СКО по кластерам, ищем момент, когда оно было минимальным. В рамках нашей задачи формирование кластеров облегчается тем, что нам не надо перебирать все варианты, а ограничиваемся лишь двумя кластерами, которые расположены последовательно, т.е. к кластерам поочередно относим часть точек начала выборки и оставшуюся часть.
∇CKO
[0] c←k CKO x;m1;m2;s1;s2
[1] m1←+/k↑x÷k
[2] m2←+/k↓x÷(⍴x)-k
[3] s1←+/+/¨((k↑x)-m1)*2
[4] s2←+/+/¨((k↓x)-m2)*2
[5] c←s1+s2
[6] ∇
ck←(⍳58)CKO¨⊂⊂[2]s
ck⍳⌊/ck
34 – все спектры до 34 относятся к 1-му классу, после – ко 2-му.
ap207.plot ck
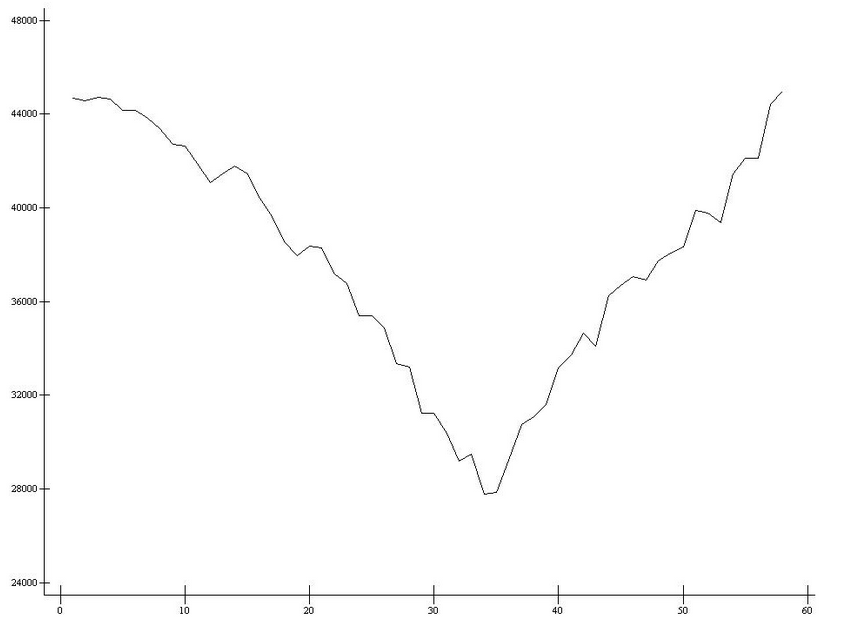
Метод k-средних
Алгоритм
метода:
![]() -
выборка из N векторов. Число кластеров
k. Начальные центры кластеров выбираются
случайным образом:
-
выборка из N векторов. Число кластеров
k. Начальные центры кластеров выбираются
случайным образом:
![]() (k
случайных точек выборки).
(k
случайных точек выборки).
Данные N векторов относим к k классам по минимальным расстояниям.
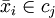 если
если
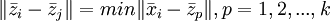 cj-j-ый
кластер,p-номер центра.
cj-j-ый
кластер,p-номер центра.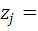
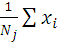 -
переоценка
центров.
-
переоценка
центров.
Шаги 2 и3 выполняем до того момента, когда центры перестанут меняться.
В нашем случае дана выборка из N точек (спектров(N=40)). Каждая из них обладает 200 признаками (200 частот). Число кластеров заранее известно - «норма» и «кризис» (к=2). Выбирая любые точки выборки, задаем начальные центры этих кластеров. Точки, оказавшиеся ближе к одному из центров, относим в соответствующий кластер. Ищем центр уже среди набранных точек. Смотрим, какие точки отнеслись к новым центрам. Снова пересчитываем центры. Совершаем процедуру до тех пор, пока центры перестанут меняться.
∇Kmean
[0] M←k Kmean x;c;M1;r
[1] M1←x[k?⍴x]
[2] L:M←M1
[3] R←+/¨(x∘.-M)*2
[4] c←(⊂[2]R)⍳¨⌊/R
[5] c←(⍳k)∘.=c
[6] M1←(⊂[2]c+.×⊃x)÷+/c
[7] →(~M≡M1)/L
[8] ∇
∇Class
[0] c←m Class x;r
[1] r←+/¨(x∘.-m)*2
[2] c←(⊂[2]r)⍳¨⌊/r
[3] ∇
m←2 Kmean⊂[2]s – результат – вектор векторов
+ck←m Class ⊂[2]s
2 2 1 1 1 2 1 1 1 1 1 1 2 2 1 1 1 1 1 2 2 1 1 1 2 1 1 2 1 2 1 1 2 1 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
+/1 2∘.=ck
24 35
ap207. plot(⍳↑⍴s)c(-ck)
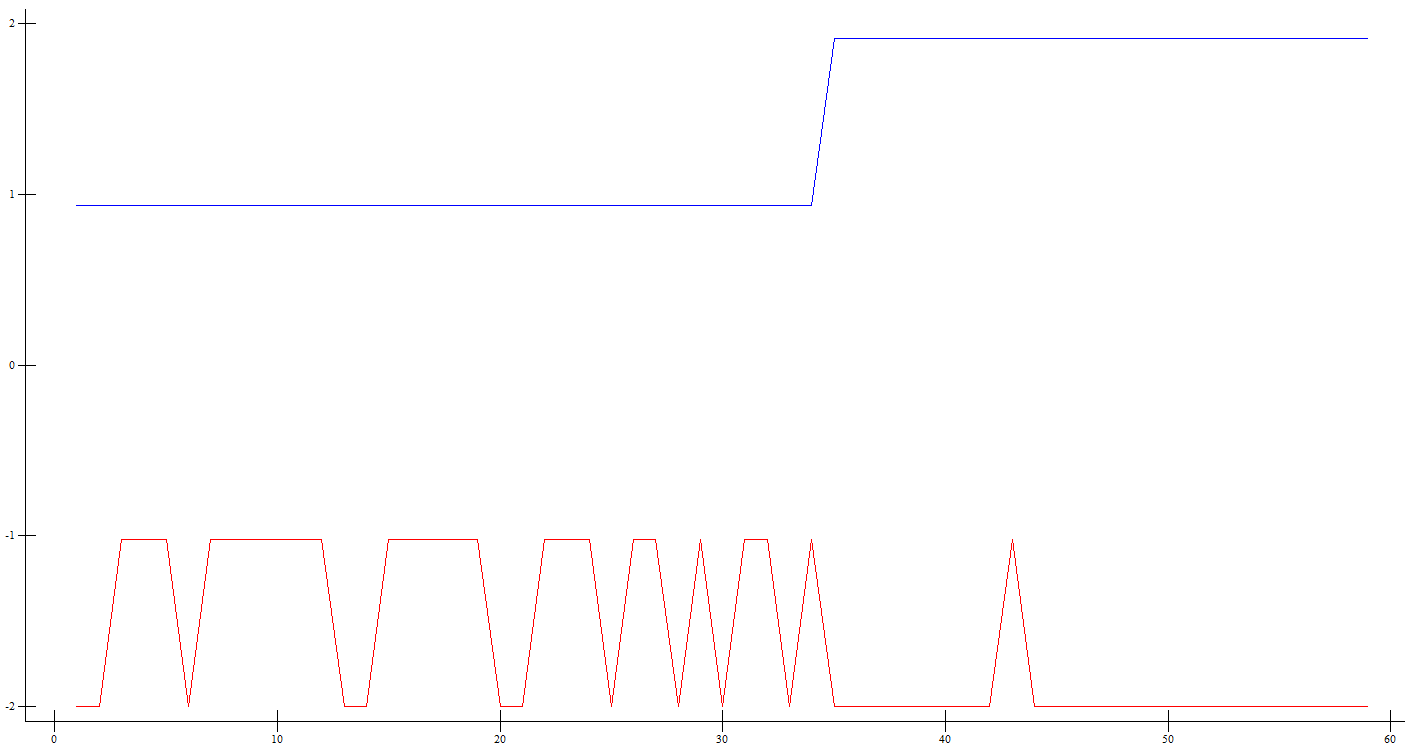
c≡ck
0
+/c≠ck
12 – ошибок
Форель
Предположительно кластер близок по распределению точек в пространстве к сферической форме. Поэтому алгоритм Форель (Центроидный метод) основывается на постепенном улучшении положение центра кластера. В этом алгоритме на каждом шаге строится сфера определенного заранее радиуса, выделяются элементы кластеризуемой совокупности, попадающие в эту сферу, и новый центр кластера строится как центр тяжести выделенных элементов. Алгоритм заканчивает классификацию, когда центр кластера приобретает устойчивую структуру (перестаёт двигаться), точки на этот момент попавшие в сферу и составляют кластер (исключаются из основной выборки). При анализе алгоритма «Форель» возникает проблема: завершится ли процесс улучшения положения центра кластера через конечное число шагов или же он может быть бесконечным т.к. центры новых сфер определяются как квадрат евклидова расстояния. В нашей задаче это не сказывается по причине малого объема данных.
В нашем случае таких кластеров 2: "Норма" и "Кризис". Берем нашу функцию и меняя значение левого аргумента, добиваемся того, чтобы в результате функция дала 2 центра (2 200-мерные точки, они же 2 спектра)
∇Forel
[0] M←R Forel X;I;M1;r
[1] M←X[1]
[2] L:M1←M
[3] r←R≥(+/¨(X-M1)*2)*0.5
[4] M←+/(r/X)÷+/r
[5] →(~M1≡M)/L
[6] →(0=⍴X←(~r)/X)/0
[7] M←M,R Forel X
[8] ∇
∇fclass
[0] c←R fclass x;m
[1] (x m)←x
[2] c←⍳0
[3] L:c←c,⊂((R*2)≥+/¨(x-m[1]*2))/⍳⍴x
[4] →(0<⍴m←1↓m)/L
[5] ∇
∇c←R FClassV x;M;c1;v
[1] (xM)←x
[2] c←⍳0
[3] L: c1←((R*2)≥+/¨(x-⊂↑M)*2)/⍳⍴x
[4] c←c,⊂c1~∊c
[5] →(0<⍴M←1↓M)/L
[6] c←((∊⍴¨c)\⍳⍴c)[⍋∊c]
∇
⍴f←40 Forel ⊂[2] s
2
⍴f←37 Forel ⊂[2] s
4
⍴f←38 Forel ⊂[2] s
2
⍴f←55 Forel ⊂[2] s
2
Как видим, при значениях радиуса гипер-сферы, начиная с 38 и заканчивая 55, у нас получается 2 центра. Это то, что нам нужно. Берем средний радиус. Например, 45,и подставляем этот результат в функцию FClass, чтобы оценить, какие точки (спектры) к какому класу отнеслись.
cf← 80 FClass (⊂[2]s)f
⊃⍕¨cf
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 45 46 47 48 49 50 51 52 53 55 56 58 59
