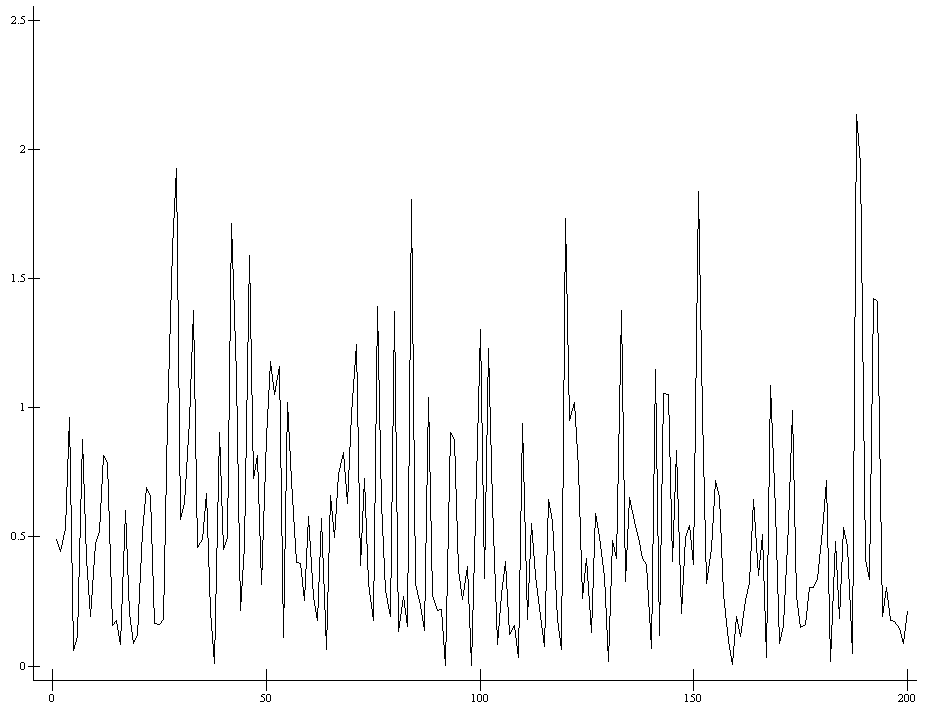
Пики по второй пройзводной.

∇deriv2ls

[0] y←n deriv2ls x;t;k

[1] t←(⍳n)-0.5×n+1

[2] k←(+/t*2)-n×t*2

[3] k←2×k÷((+/t*2)*2)-n×+/t*4

[4] y←k+.×(-n-1)↓[2](¯1+⍳n)⌽(n,⍴x)⍴x

[5] n←0.5×n-1

[6] y←(n⍴↑y),y,n⍴¯1↑y

[7] ∇

ap207.plot (⍳⍴s1) s1 (5 deriv2ls s1)

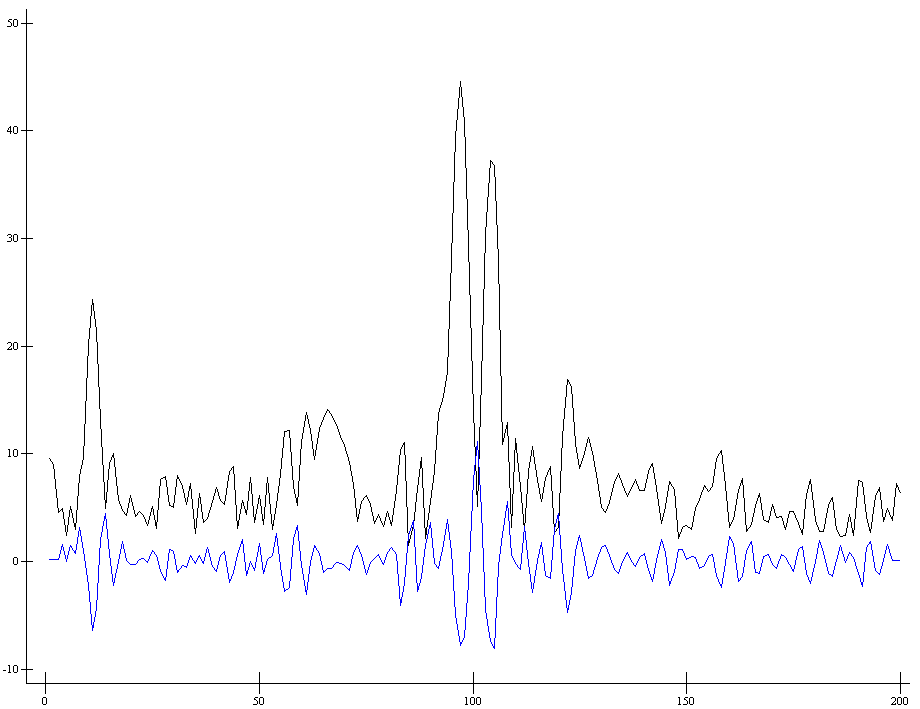
ap207.plot (⍳⍴s1) s1 (11 deriv2ls s1)

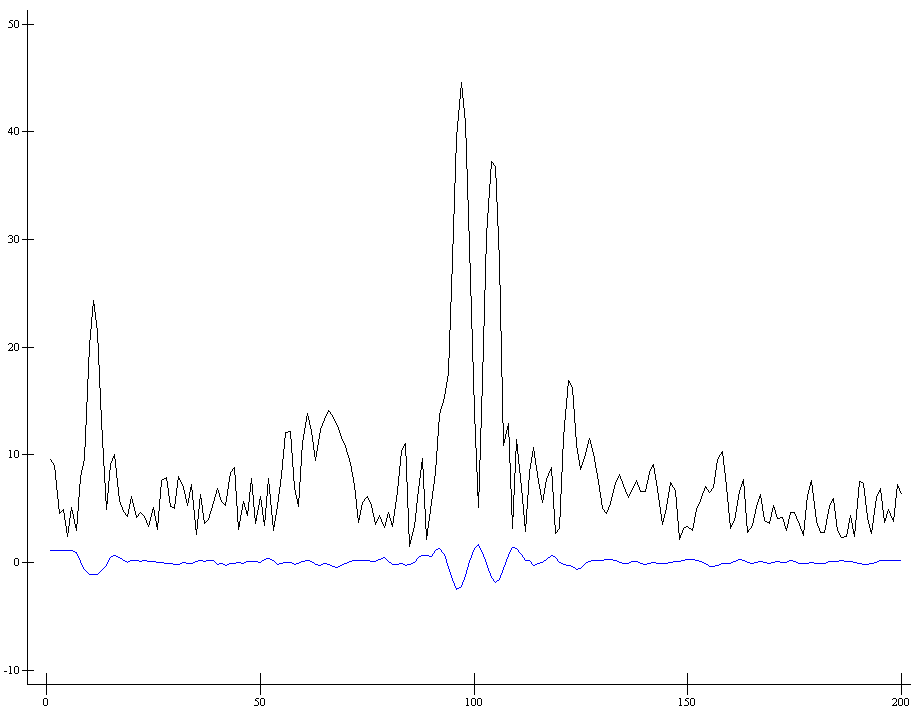
d←⊃5 deriv2ls¨⊂[2]s

+/∨⌿¯3>d

39

f←( ∨⌿¯3>d)/⍳200

m1←+⌿34↑[1]s÷+/c=1

m2←+⌿34↓[1]s÷+/c=2

Ослабить требования к «на всех нормах» «ни на одном кризисе»

i←⊃3(⍴ GoodPeaks) ¨⊂[2]s

j←⊃10(+/ GoodPeaks) ¨⊂[2]s

A←+⌿34↑[1]i

B←+⌿34↓[1]i

f←20↑⍒|A-B

6 наилучших частот

6↑⍒|A-B

141 94 125 20 56 96

f←6↑⍒|A-B

0 ap207.plot ((⍳k)(k↑s[;94]))((k↓⍳↑⍴s)(k↓s[;94]))

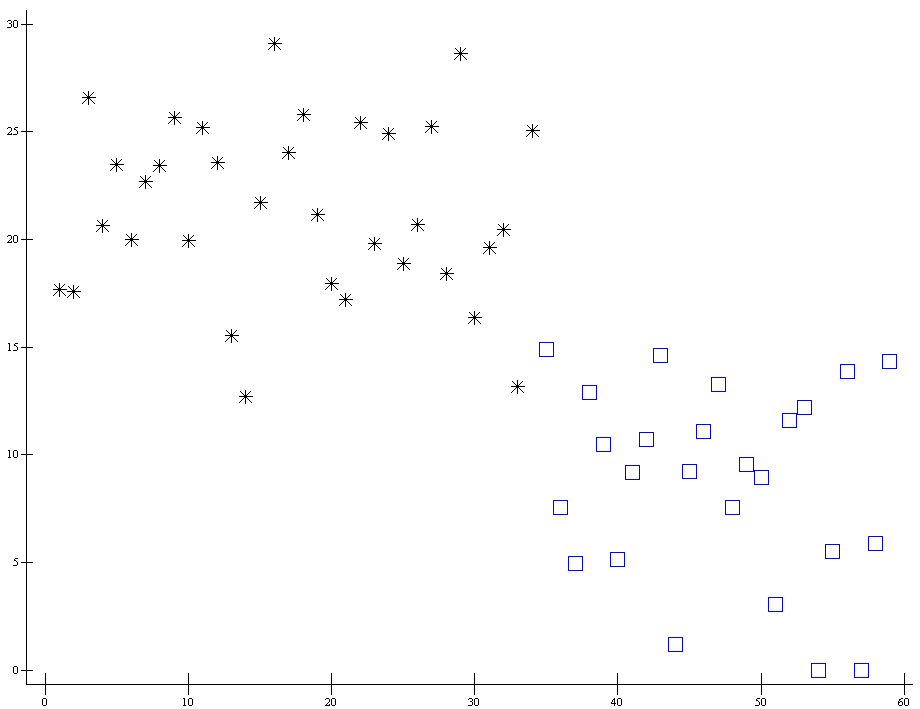
0 ap207.plot (⊂[1]k↑[1]s[;94 141])(⊂[1]k↓[1]s[;94 141])

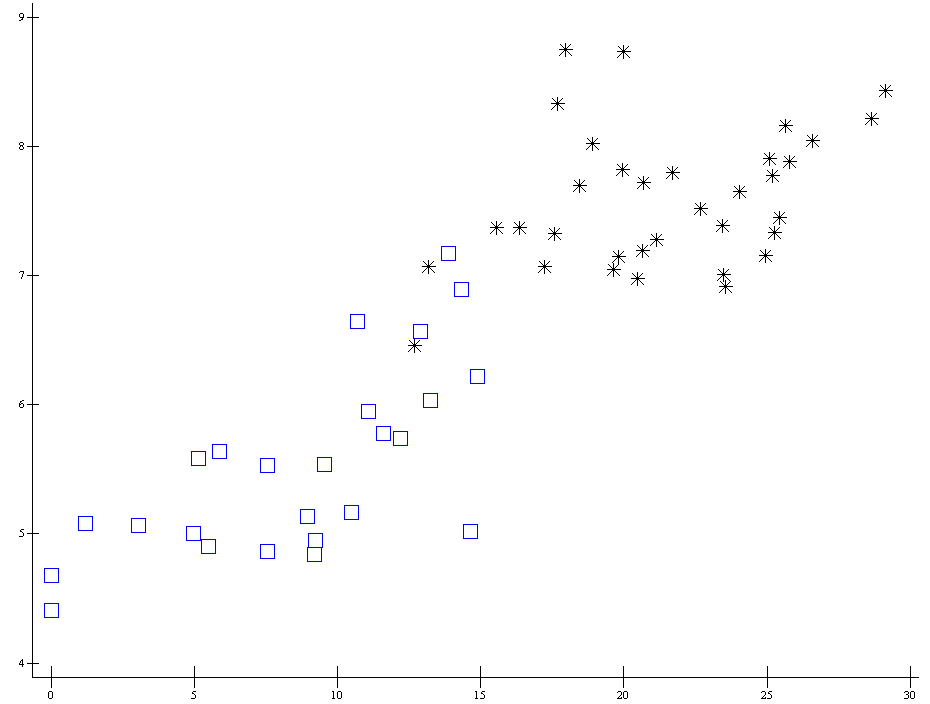
Фишер

Одномерный Фишер:

∇fisher1

[0] f←a fisher1 b;m1;m2;s1;s2

[1] m1←+/a÷⍴a

[2] s1←+/(a-m1)*2

[3] m2←+/b÷⍴b

[4] s2←+/(b-m2)*2

[5] f←((m1-m2)*2)÷s1+s2

[6] ∇

ap207.plot (⊂[1]34↑[1]s) fisher1¨⊂[1]34↓[1]s

∇fisher2

[0] f←a fisher2 b;m1;m2;s1;s2

[1] m1←0.5 quint a

[2] s1←(0.75 quint a)-0.25 quint a

[3] m2←0.5 quint b

[4] s2←(0.75 quint b)-0.25 quint b

[5] f←(|m1-m2)÷s1+s2

[6] ∇

ap207.plot (⊂[1]34↑[1]s) fisher2¨⊂[1]34↓[1]s

f1←(⊂[1]34↑[1]s) fisher1¨⊂[1]34↓[1]s

f2←(⊂[1]34↑[1]s) fisher2¨⊂[1]34↓[1]s

10 наилучших частот(на которых критерии Фишера максимальны):

10↑⍒f1

188 189 28 29 42 76 84 120 46 151

10↑⍒f2

188 189 29 151 84 120 42 28 46 192

(10↑⍒f1)∩10↑⍒f2

188 189 28 29 42 84 120 46 151

0 ap207.plot(34↑¨(s[;188])(s[;189]))(34↓¨(s[;188])(s[;189]))

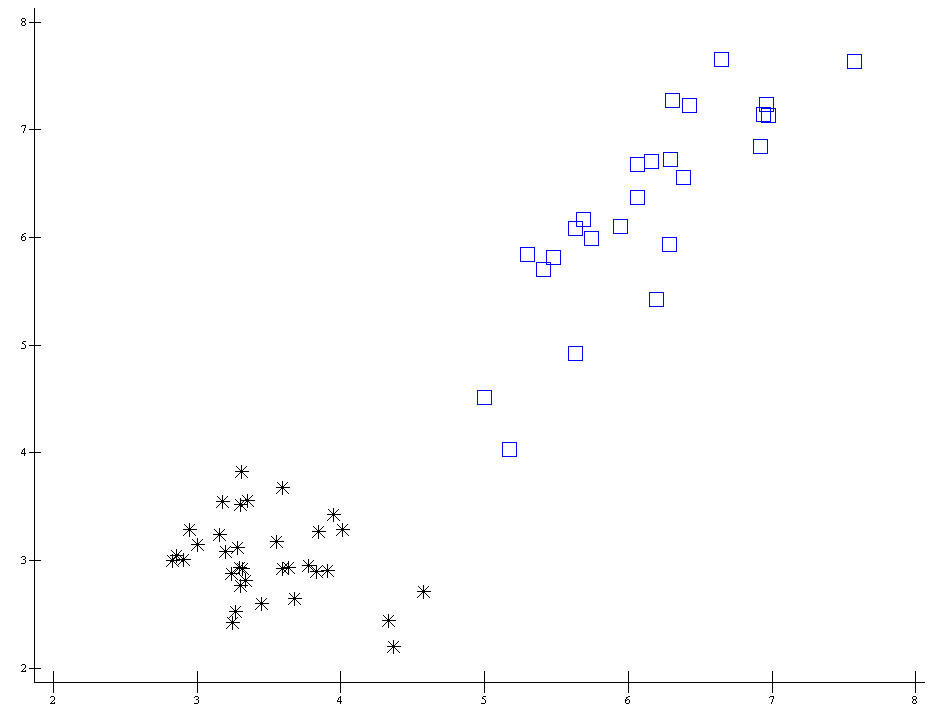
сравнение параметрического и непараметрического:

∇norm

[0] y←norm x

[1] y←x÷⌈/x

[2] ∇

ap207.plotn (⊂⍳200),norm¨f1 f2

Многомерный критерий Фишера:

∇fisher

[0] d←y fisher x;s1;s2;m1;m2

[1] m1←(+⌿x)÷↑⍴x

[2] m2←(+⌿y)÷↑⍴y

[3] s1←(⍉s1)+.×s1←x-(⍴x)⍴m1

[4] s2←(⍉s2)+.×s2←y-(⍴y)⍴m2

[5] d←(m1-m2)+.×⌹s1+s2

[6] ∇

do←(c=1)⌿s

po←(c=2)⌿s

Понижаем размерность признаков:

⍴s1←+/34 10 20 ⍴do

34 10

⍴s2←+/25 10 20 ⍴po

25 10

fi←s1 fisher s2 -координаты вектора в 10-ти мерном пространстве

30 ap207.hist2(fi+.×⍉s1)(fi+.×⍉s2) – гистограмма значений проекций в 10-ти мерном пространстве

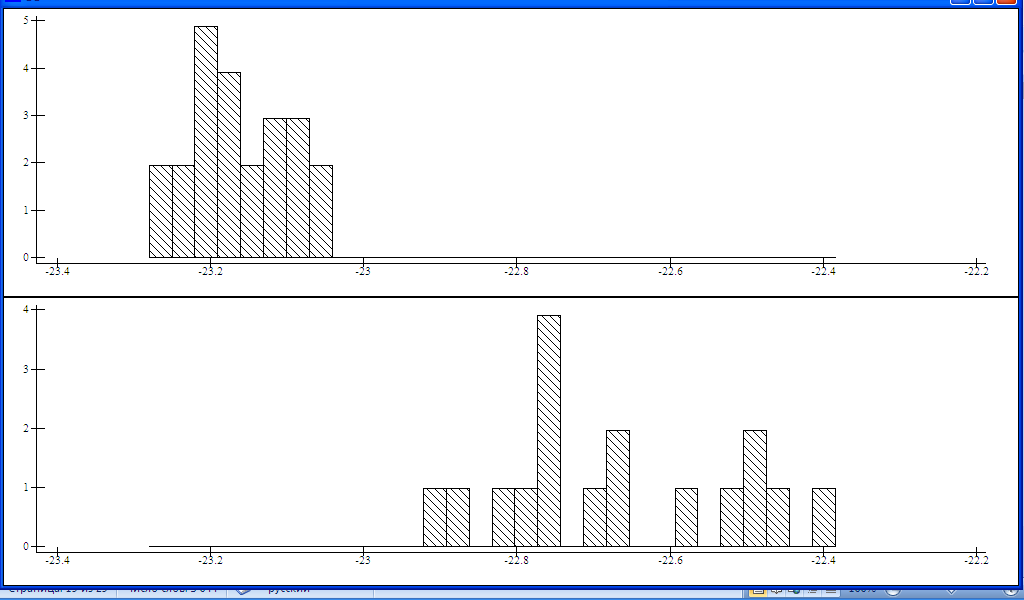
Расстояние от двух фиксированных точек

Расстояние от 2-х фиксированных точек-метод классификации данных.

Алгоритм:

1.Вычисляем центры классов (средние значения нормы и кризиса).

2.Для каждого спектра вычисляем расстояние до центров классов, спектры, соответствующие норме должны быть ближе к среднему по норме, спектры, соответствующие кризису должны быть ближе к среднему по кризису.

Функция dist вычисляет расстояние между средним спектром и вектором векторов всех спектров.

∇dist

[0] r←y dist x

[1] r←(+/¨(y-⊂x)*2)*0.5

[2] ∇

a←⊂[2]34↑[1]s

b←⊂[2]34↓[1]s

m1←↑+/a÷⍴a

m2←↑+/b÷⍴b

m1 и m2 – средние значения по всем спектрам до и после – фиксированные точки.

data_a←(a dist m1) (a dist m2)

data_b←(b dist m1) (b dist m2)

0 ap207.plot data_a data_b

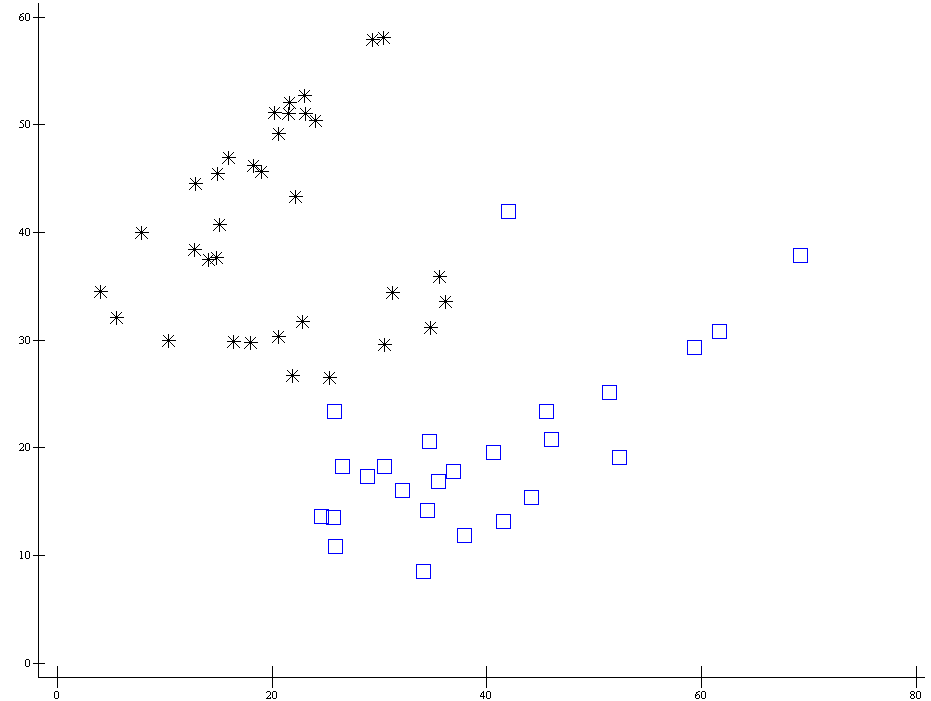
Линейное шкалирование Орлочи

Первая ось Орлочи - линия, соединяющая две самые удалённые точки неклассифицированных данных.

x←⊂[2]s

r←+/¨(x∘.-x)*2

1+(⍴r)⊤¯1+(,r)⍳⌈/,r

6 37– минимальный и максимальный спектры

m1←↑x[6]

m2←↑x[37]

datax←(x dist m1) – ось абсцисс

datay←(x dist m2) - ось ординат

Проекция на плоскость Орлочи:

Вторая ось – перпендикулярна к первой оси и максимально от неё удалена.

∇Orloci

[0] r←Orloci x;a;i;j;k

[1] r←+/¨(x∘.-x)*2

[2] (i j)←1+(⍴r)⊤¯1+(,r)⍳⌈/,r

[3] x←x-x[i]

[4] a←(+/¨x×x[j])÷+/↑x[j]*2

[5] r←+/¨(x-aרx[j])*2

[6] x←x-x[j]×a[k←r⍳⌈/r]

[7] r←+/¨x[j,k]∘.×x

[8] ∇

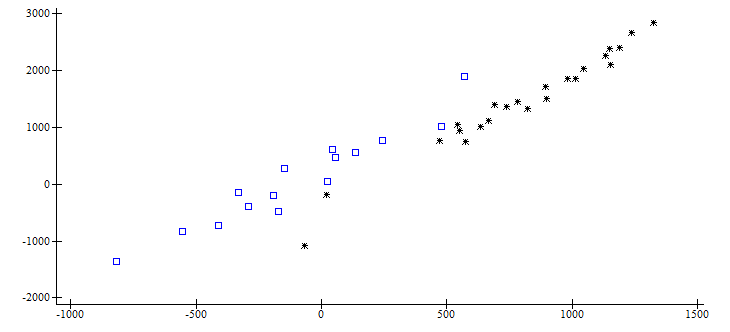0 ap207.plot (34↑¨⊂[2] Orloci x ) (34↓¨⊂[2] Orloci x )

Метод Главных компонент

Метод Главных Компонент — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных.

 - оси координат в данном пространстве

 - вектора в данном пространстве

Условия ортогональности осей:

 

  

 - сумма всех векторов - 0-вектор(центрирование)

-нормирование

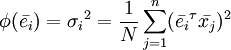 - вес оси 

Задача метода - повернуть систему координат так, чтобы распределение весов было максимально неравномерно.

Энтропия - лучшая мера изменчивости весов. Она уменьшается с увеличением неравномерности, значит нужно минимизировать энтропию.

Максимальная энтропия соответствует равномерному распределению.

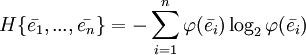
Минимальная энтропия достигается, если в качестве координат взять собственные вектора корреляционной матрицы.

Найдём:

l- вектор собственных значений

V - собственные вектора

Pr - проекцию с помощью функции Selfic.

s←+/59 10 20 ⍴s

e←mds.(CORM SELFIC) s

l←↑e

⍴e

3

+\l÷+/l

0.575209861 0.9082808202 0.9878576379 0.9998139832 0.9999837411 0.9999929794 0.9999999241 1 1 1

0 ap207.plot 100 × +\l÷+/l

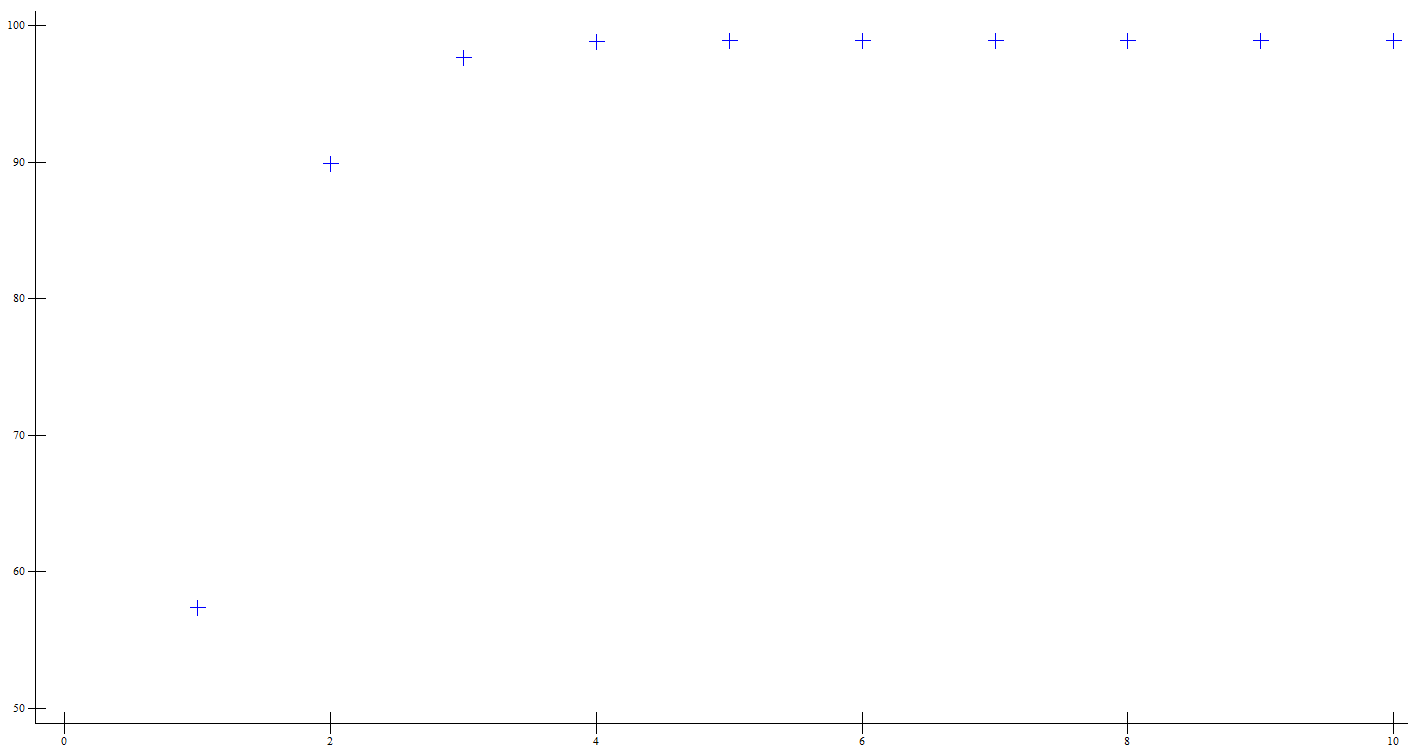
Возьмём проекции

Pr←3⊃e

⍴Pr

59 10

Строим проекции на плоскости двух главных компонент:

0 ap207.plot k {(⍺↑¨⍵)(⍺↓¨⍵)}⊂[1]Pr[;1 2]