
Линейные операции:
Сложение: сумма двух векторов – третий вектор, направленный из начала первого вектора в конец второго.
Умножение вектора на число – вектор, параллельный первому вектору, модуль его равен модулю, умноженному на число и если число отрицательное, то меняется направление вектора.
18
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.
Векторы коллинеарны, если существует прямая которой они параллельны.
Лемма:
если вектор b
коллинеарен ненулевому вектору a,
то
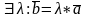
Если
вектор b
компланарен с некоторыми векторами
a1,a2,
то существует единственное разложение
в виде линейной комбинации векторов
a1,a2
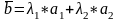
Доказательство: существование:

Рассмотрим
OP
и OQ,
 по
правилу параллелограмму,
по
правилу параллелограмму,
 //
//
 ,
,
 по
лемме
по
лемме
 .
Аналогично,
.
Аналогично,
 .
.
Единственность:
предположим, что

Тогда
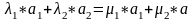 ,
,
 .
Т.к. разложение различное, то одна из
скобок отлична от нуля. Пусть это будет
первая скобка, разделим на неё, получим:
.
Т.к. разложение различное, то одна из
скобок отлична от нуля. Пусть это будет
первая скобка, разделим на неё, получим:
 ,
что противоречит условию. Доказано.
,
что противоречит условию. Доказано.
Если
a1,a2,a3
– некомпланарные вектора, то для любого

 разложение
в виде линейной комбинации векторов
a1,a2,a3,
т.е.
разложение
в виде линейной комбинации векторов
a1,a2,a3,
т.е.
 .
Доказательство: Во многом похоже на
предыдущее.
.
Доказательство: Во многом похоже на
предыдущее.
19
Базис на плоскости – упорядоченная пара неколлинеарных векторов.
Базис в пространстве – упорядоченная тройка неколлинеарных векторов.
Орт – единичный вектор.
Совокупность т.O и ортонормированного базиса i,j,k, приложенного к т.O, называют прямоугольным(декартовым) системой координат, т.O – начало координат, а базисные векторы задают направления осей.
Деление отрезка в заданном отношении:

 -
известно.
-
известно.
 ,
,
 .
.

20
Проекция вектора a равна произведению длины вектора на косинус угла между вектором и направляющим вектором.
прea=
 .
.
Доказательство: возможны три случая:
Угол острый:
п рL
рL ,
из треугольника
ABB1:
,
из треугольника
ABB1:
Угол прямой:

прL
Угол тупой:
п рL
рL
21
Скалярным
произведением
вектора a
на вектор b
называется число(скаляр)

Свойства скалярного произведения:
1.
( )≥0.
Доказательство: (
)
=
)≥0.
Доказательство: (
)
=
 *
*Cos0
=
2≥0.
Доказано.
*
*Cos0
=
2≥0.
Доказано.
2.
( )
= (
)
= ( ).
Доказательство: очевидно.
).
Доказательство: очевидно.
3. (a,b+c)=(a,b)+(a,c). Доказательство: воспользуемся связью между проекциями: (a,b+c)=|a|*прa(b+c)=|a|*(прab+прac)=|a|*прab+|a|*прac=(a,b)+(a,c).
4.
 Доказательство: воспользуемся связью
между проекциями:
Доказательство: воспользуемся связью
между проекциями:
 .
.
22
Векторным
произведением
вектора a
на вектор b
называется вектор c
=

Свойства векторного произведения:
[a,a] = 0.
[a,b]=-[b,a].
[(a+b),c]=[a,b]+[a,c].
[a,[b,c]]=b(a,c)-c(a,b).
23
Смешанное
произведение
– скалярное произведение вектора a
на векторное произведение вектора b
на вектор c.
 .
.
Свойства смешанного произведения:
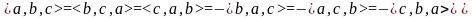

Если 3 вектора коллинеарные (т.е. лежат в одной плоскости), то их смешанное произведение равно 0.
24
Прямая на плоскости:
Общее уравнение: Ax+By+C=0, координаты вектора нормали (A,B).
Уравнение
прямой в отрезках:
 .
.
Нормальное
уравнение прямой:
 ,
где
,
где
 -
угол между прямой и осью икс,
-
угол между прямой и осью икс,
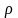 -
расстояние от начала координат.
-
расстояние от начала координат.
Каноническое
уравнение прямой:

Уравнение
прямой через две точки:

Уравнение
прямой по точке и угловому коэффициенту:
 или y
= kx
+ b.
или y
= kx
+ b.
Параметрическое
уравнение прямой:

25
Взаимное расположение прямых:
Лежат
на одной прямой,
если
 .
.
Параллельны,
если

Пересекаются,
если
 .
.
Угол
между прямыми
фактически равен углу между нормалями
прямых:
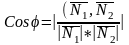 ,
,
 .
.
Условия
перпендикулярности:
прямые перпендикуляры, если перпендикулярны
их нормали, т.е. если

Расстояние
от точки до прямой на плоскости:

26
Плоскость в пространстве:
Общее уравнение: Ax+By+Cz+D=0, координаты нормали (A,B,C).
Уравнение
плоскости в отрезках:
 .
.
Каноническое
уравнение плоскости:

Уравнение
плоскости через две точки:
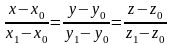
Параметрическое
уравнение плоскости:

27
Взаимное расположение плоскостей:
Лежат
в одной плоскости,
если
 .
.
Параллельны,
если

Пересекаются,
если

Угол
между плоскостями:
фактически равен углу между нормалями
плоскостей:

Условия
перпендикулярности:
плоскости перпендикуляры, если
перпендикулярны их нормали, т.е. если

Расстояние
от точки до плоскости в пространстве:
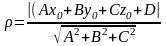
28
Прямая в пространстве:
Общее уравнение: Ax+By+Cz+D=0, координаты нормали (A,B,C).
Уравнение прямой в отрезках: .
Каноническое уравнение прямой:
Уравнение прямой через две точки:
Параметрическое уравнение прямой:
29
Расстояние от точки до прямой в пространстве:
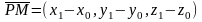


Расстояние между скрещивающимися прямыми:


Угол между прямыми в плоскости фактически равен углу между направленными векторами:

Угол между прямой и плоскостью:


30
Линейное векторное пространство – это непустое множество L элементов, в котором:
Для любых x,y определена сумма, принадлежащая этому пространству.
Для любого x и , принадлежащим этому пространству, определено
 ,
при этом накладываются следующие
условия:
,
при этом накладываются следующие
условия:
 ,
для любых
,
для любых  (коммутативность
сложения);
(коммутативность
сложения); ,
для любых
,
для любых  (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что  для
любого
для
любого  (существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;
(существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;для любого существует такой элемент
 ,
что
,
что  (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения). (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр); (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Свойства линейного векторного пространства:
Нейтральный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
. для
любых
для
любых  и
.
и
. для
любого
.
для
любого
.
31
Линейная зависимость векторов линейного пространства:
Размерность линейного пространства: линейное пространство V называется n-мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n + 1 векторов линейно зависима.
Базис - любая упорядоченная система e1,e2,…,en из n линейно независимых векторов пространства Vn.
32
Базис - любая упорядоченная система e1,e2,…,en из n линейно независимых векторов пространства Vn.
33
Подпространство линейного пространства – не пустое подмножество L1 его элементов, само являющееся линейным пространством относительно введенных в L операций сложения векторов и умножения на число.
Для
проверки того, что подмножество L1
является подпространством множества
L
необходимо и достаточно убедиться, что

34
Пусть
L
– линейное пространство. Скажем, что в
L
задано скалярное
произведение,
если в каждой паре векторов x,y,
принадлежащих этому линейному
пространству, поставлено в соответствие
скалярное произведение x,y
принадлежащих R
так, что
 выполняются
условия:
выполняются
условия:

Евклидовым
линейным пространством
называется пространство со скалярным
произведением, удовлетворяющим условию:
 и
равенства
и
равенства

Теорема
Пифагора:
если векторы x,y
ортогональны, то квадрат нормы
 .
.
Доказательство:
т.к. x┴y,
то (x,y)=0,
тогда
 Неравенство
Коши-Буняковского:
в любом евклидовом пространстве
Неравенство
Коши-Буняковского:
в любом евклидовом пространстве
 выполняется
неравенство
выполняется
неравенство
 .
.
Доказательство:
пусть
 .
Тогда для вектора
.
Тогда для вектора


Получим
квадратных трехчлен относительно
.
Он должен быть ≥0, значит он не может
иметь двух различных корней, => D
≤0 =>

Доказано.
Неравенство
треугольника:
в евклидовом пространстве для

Доказательство:
 по
неравенству Коши-
Буняковского
по
неравенству Коши-
Буняковского
 .
Извлечем корень, получим
.
Извлечем корень, получим
 .
Доказано.
.
Доказано.
35
Базис e1,e2,…,en евклидового пространства L называется ортонормированным, если (ei,ej)=0 при i≠j.
Линейная независимость системы попарно ортогональных ненулевых векторов: попарно ортогональные и отличные от нуля векторы линейно независимы.
Доказательство:
