
Разложение определителя:
Минором Mij называется aij определителя n-ого порядка называется определитель n-1 порядка, полученного из исходного определителя путем вычеркивания i-ой строки и j-ого столбца.
Алгебраическим дополнением Aij элемента aij называется его минор, взятый со знаком (-1)i+j.
по элементам i-й строки:
![]()
по элементам j-го столбца:
![]()
8
Обратная матрица – такая матрица, которая при умножении на саму матрицу дает единичную матрицу (A * A-1 = E).
Единственность – если матрица не вырождена (т.е. определитель не равен нулю), то для неё существует одна обратная матрица.
Доказательство: Пусть матрицы B и C - обратные матрицы для A. Тогда:
BAC = (BA)C = EC = C
BAC = B(AC) = BE = B => B = C. Доказано.
Критерий обратимости – чтобы матрица была обратима, необходимо и достаточно, чтобы она была не вырождена.
Доказательство:
необходимость: матрица А обратима, т.е.
существует A-1
такая, что A
* A-1
= A-1
*
А = Е. Надо доказать, что det
A
≠ 0. Рассмотрим
det(A * A-1)
= det(A-1
*
А)
= det E = 1. det A * det A-1
= 1 det
A ≠ 0, det A-1
≠ 0.
det
A ≠ 0, det A-1
≠ 0.
Достаточность:
Пусть А не вырождена, т.е. det
A
≠ 0. Рассмотрим
 Докажем, что матрица В есть обратная
матрица А, т.е. А * В = В * А = Е.
Докажем, что матрица В есть обратная
матрица А, т.е. А * В = В * А = Е.


9
Обратная матрица – такая матрица, которая при умножении на саму матрицу дает единичную матрицу (A * A-1 = E).
Некоторые свойства обратной матрицы:
E-1 = E, т.к. E * E = E
det(A-1) =
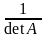
(A-1)-1=A, т.к. A-1*А= А* A-1=E.
(AT)-1=(A-1)T, т.к. (A-1)T*AT= (A*A-1)T=ET=E;
AT*(A-1)T=(A*A-1)T=E.
(A*B)-1=B-1*A-1,т.к. (B-1*A-1)*AB= B-1*A-1*A*B=B-1*E*B=E;
AB*(B-1*A-1)= A*B * B-1*A-1 =A-1*E*A=E.
Вычисление с помощью элементарных преобразований:
Если определитель исходной матрицы не равен нулю, то
Вычисляем алгебраические дополнения Aij.
Составляем присоединенную матрицу C =

Находим
 =
CT
=
CTA-1=1/detA*
Если определитель исходной матрицы равен нулю, то обратной матрицы нет.
10
Рангом матрицы А называют наивысший порядок, отличный от нуля минора этой матрицы (лекции).
Ранг матрицы А равен k, если среди миноров этой матрицы есть по крайней мере один отличный от нуля минор k-ого порядка, а все её миноры порядка k+1 и выше либо равны 0, либо не существуют.
Ранг ступенчатой матрицы равен числу её строк.
Доказательство:
Рассмотрим матрицу А:

Составим минор порядка m, выбрав столбцы, нулевые элементы которых стоят внутри ступенек. Получим минор M размера mxm:
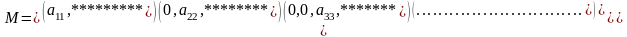
r(A) = m, т.е. числу ступенек.
При элементарных преобразованиях над строками/столбцами матрицы её ранг не изменяется.
Доказательство: рассмотрим каждое элементарное преобразование в отдельности. При умножении любой строки на число, не равное нулю, миноры этой матрицы не изменяются и очевидно, что наивысший порядок в минорах не изменится. При перестановке 2х строк местами изменившиеся миноры поменяют знак. При умножении одной строки на любое число и добавления её к другой строке:

Пусть
ранг А = k,
покажем, что ранг B k.
Для этого достаточно показать, что
каждый минор матрицы В порядка выше,
чем k
= 0. Пусть D
– минор матрицы В порядка выше, чем k.
Возможны 3 различных случая:
k.
Для этого достаточно показать, что
каждый минор матрицы В порядка выше,
чем k
= 0. Пусть D
– минор матрицы В порядка выше, чем k.
Возможны 3 различных случая:
Детерминант минора не содержит i-ой строки матрицы В. В этом случае D совпадает с соответствующим минором матрицы А, т.к. ранг матрицы А = k, то D = 0.
D содержит i и j строки: По 9 свойству детерминанта(детерминант не изменится, если к любой строке добавить другую строку, умноженную на число) определитель(минор) не изменится, т.е. равен соответствующему минору матрицы А = 0.
D содержит i строку и не содержит j строку. Тогда по свойству D = D1+D2. D1 совпадает с минором матрицы А и равен нулю. А D2 – то, что осталось от остальных слагаемых и равен соответствующему минору матрицы А, умноженной на
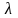 и
равно 0 => D
= 0 => r(B)
= r(A)
= k.
Доказано.
и
равно 0 => D
= 0 => r(B)
= r(A)
= k.
Доказано.
11
Строки
 матрицы
А линейно
зависимы,
если можно подобрать такие числа
k1,k2,…,kn,
не равные нулю одновременно, что
матрицы
А линейно
зависимы,
если можно подобрать такие числа
k1,k2,…,kn,
не равные нулю одновременно, что
 ,
где 0 – нулевая строка.
,
где 0 – нулевая строка.
Теорема о ранге матрицы: Если ранг матрицы А равен k, то в этой матрице можно найти k линейно независимых строк, через которые линейно выражаются все остальные строки.
Доказательство:
пусть дана матрица А mxn
и пусть r(A)
= k
и пусть D
– минор k-ого
порядка ≠ 0. Такой минор называется
базисным. Для определенности будем
считать, что он расположен в левом
верхнем углу. Покажем, что первые k
строк матрицы А линейно независимые.
Предположим противное, что одна из строк
линейно выражается через остальные,
т.е.
 .
Умножим первую строку на (-c1)
и прибавим её к k-ой
строке. Умножим вторую строку на (-c2)
и прибавим её к k-ой
строке. И так далее до k-ой
строки. В итоге получим, что определитель
базисного минора равен нулю, что
противоречит условию. Доказано.
.
Умножим первую строку на (-c1)
и прибавим её к k-ой
строке. Умножим вторую строку на (-c2)
и прибавим её к k-ой
строке. И так далее до k-ой
строки. В итоге получим, что определитель
базисного минора равен нулю, что
противоречит условию. Доказано.
12
Правило Крамера:
Если определитель квадратной матрицы не равен нулю, то её решение можно найти по формуле Крамера:

13
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Теорема Кронекера-Капелли. Произвольная система линейных уравнений совместна тогда и только тогда, когда r(A) = r( ).
Доказательство:
Необходимость:
Пусть система совместна и x1
=
 ,
x2
=
,
x2
=
 ,…,
xn
=
,…,
xn
=
 - некоторые решения, подставив
,
,…,
- получим тождество:
- некоторые решения, подставив
,
,…,
- получим тождество:

Столбцы
свободных членов являются линейной
комбинацией столбцов матрицы А системы.
Прибавим к последнему столбцу матрицы
 её первый столбец, умноженный на (-
),
умножим второй столбец на (-
)
и добавим к последнему и так далее до n
включительно. В итоге получим матрицу
С вида:
её первый столбец, умноженный на (-
),
умножим второй столбец на (-
)
и добавим к последнему и так далее до n
включительно. В итоге получим матрицу
С вида:

r(C)
= r( ),
r(C) = r(A) => r(
)
= r(A).
),
r(C) = r(A) => r(
)
= r(A).
Достаточность: пусть r( ) = r(A) = k. Для определенности предположим, что определитель k-ого порядка не равен 0 и расположен в левом верхнем углу:

Тогда первые k строк матриц А и линейно независимые, а остальные можно выбросить, т.к. они являются их линейной комбинацией.
Возможно два случая:
1. k = n. Тогда можно решить методом Крамера.
2. k<n. Тогда в левой половине оставим k неизвестных, а остальные перенесем вправо. Неизвестные этого минора мы назовем базисными, а остальные - свободные. Свободным неизвестным можно давать любые значения, получая при этом значения базисных решений. Доказано.
14
Метод Гаусса:
Привести матрицу (расширенную) к ступенчатому виду с помощью элементарных преобразований и вычеркиванием нулевых строк. Неизвестные, соответствующие базисному минору, называются базисные, остальные неизвестные – свободные.
Все свободные неизвестные перенести в правую часть каждого из уравнений.
Совершая элементарные преобразования над строками матрицы снизу вверх, превращаем матрицу в диагональную, а потом в единичную.
Таким образом базисные элементы не зависят друг от друга .
15
Однородная система - система линейных алгебраических уравнений с нулевой правой частью.
Свойства решений системы линейной однородных уравнений:
Пусть
e1 и e2
и e2 -
два любых решения однородной системы.
-
два любых решения однородной системы.
A*e1=0, A*e2=0, следовательно c*e1 – тоже решение и e1+e2 тоже решение.
Доказательство:
A*(c*e)= c (A*e) = c * 0 = 0;
A*(e1 + e2) = A*e1 + A*e2 = 0 + 0 = 0. Доказано.
Если e1,e2,…,en – произвольные решения системы, то линейные комбинации c1*e1 + c2*e2 +…+ cnen тоже будут решением.
Фундаментальная система решения (ФСР) – линейно независимые решения системы уравнений e1,e2,…,en, удовлетворяющих уравнению A*x = 0.
Теорема о существовании ФСР:
Если r(A) = k < n, то система A*x = 0 обладает ФСР.
Доказательство:
Пусть А – матрица системы:
 ,
,

Уравнения от k до n являются следствием первых k уравнений, поэтому оставим первые k уравнений. Перенесем все неизвестные за знак равенства, получим:

Пусть
 ,
тогда
,
тогда
 ,
получим:
,
получим:
( )
)
Пусть
 ,
тогда
,
тогда
 ,
получим:
,
получим:
( )
)
Пусть
 ,
тогда
,
тогда
 ,
получим:
,
получим:
( )
)
Получим n-k решений, запишем их по строке:

Минор справа не равен 0, а значит все решения линейно независимые.
Докажем, что любое решение, деленое на e будет являться линейной комбинацией:
e1 = ;
e2 = ;
……………………..........
en = ;
e0
=

Рассмотрим
матрицу e0
=
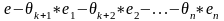 (1)
(1)
 тоже
решение.
тоже
решение.

e0 = (0;0;…;0). Подставим в (1), получим:
0
=

 ,
доказано.
,
доказано.
16
Общее решение неоднородной системы = частное решение неоднородной системы + общее решение однородной системы.
17
Вектор – направленный отрезок, один из концов которого – начало, другой – конец.
