Числовые и функциональные ряды Числовые ряды

1. Определить сходимость числового ряда

                                                    .                                               

Решение. Данный числовой ряд – сумма всех членов геометрической прогрессии с первым членом  и знаменателем   Вычисляя сумму первых  чисел, получаем:

 или .

Переходя к вычислению предела, заметим, что в зависимости от значений  и  частичная сумма ряда принимает различные значения.

1). Если , то  при 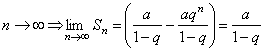. Значит, в случае ряд (98) сходится и его сумма .

2). Если , то  и тогда  при , т.е.  не существует. Таким образом, в случае  ряд (98) расходится.

3) Если , то ряд (98) имеет вид: . В этом случае , т.е. ряд расходится.

Если  то . В этом случае:

Следовательно, частичная сумма предела не имеет.

Таким образом, сумма членов геометрической прогрессии (с первым членом отличным от нуля) сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы. ►

2. Определить сходимость числового ряда .

Решение. Воспользуемся необходимым признаком сходимости ряда. Для данного числового ряда записываем формулу общего члена и вычисляем предел

.

Так как предел не равен нулю, то исходный ряд расходится. ►

Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, то есть из того, что n-й член ряда стремится к нулю, ещё не следует, что ряд сходится – ряд может и расходиться.

3. Определить сходимость числового ряда

                                                    .                                                       (104)

Решение. Для данного числового ряда записываем формулу общего члена и вычисляем предел . Необходимый признак выполнен. Докажем, однако, что исходный ряд расходится. Распишем его подробнее:

                                   (105)

и составим вспомогательный ряд:

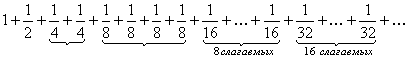              .                                   (106)

Ряд (106) строится следующим образом: его первый член равен 1, второй – , третий и четвёртый равны , члены с пятого по восьмой равны , члены с девятого по 16-й равны , с 17-го по 32-й – , и т.д.

Обозначим через Sn⁽¹⁾ сумму первых n членов гармонического ряда (105), а через Sn⁽²⁾ сумму первых n членов ряда (106). Так как каждый член ряда (105) больше соответствующего члена ряда (106), то для (n  2) выполнено

                                                         .                                                                 (107)

Подсчитаем частичные суммы ряда (106) для значений n равных степеням двойки: 2¹, 2², 2³, 2⁴, 2⁵ и т.д. Имеем:

,

,

,

,

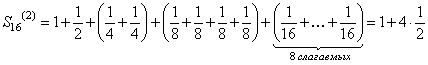Заметим, что , , и т.д. Следовательно , т.е. частичные суммы Sn⁽²⁾ при  неограниченно увеличиваются или . Но тогда из соотношения (107) следует, что . Таким образом, исходный числовой ряд расходится. Числовой ряд (104) часто называют гармоническим. ►

Пусть даны два ряда с положительными членами

                                                    ,                                                        (108)

                                                    .                                                         (109)

Для них справедливы следующие утверждения.

Теорема (Первый признак сравнения числовых рядов). Пусть члены ряда (108) не больше соответствующих членов ряда (109), т.е. при n=1, 2, ...

                                                              .                                                                   (110)

Тогда, если ряд (109) сходится, то сходится и ряд (108).