8. Центробежные моменты инерции. Эллипсоид инерции. Главные оси инерции.

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

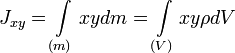
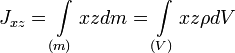
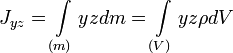
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Эллипсоид инерции

Момент инерции тела дается общей формулой:

Тензор инерции — в механике абсолютно твёрдого тела — величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью.

Тензор инерции для твердого тела представляется в виде симметричной матрицы

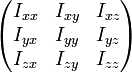
в которой элементы являются моментами инерции относительно различных осей:

Матрица тензора инерции может быть представлена в диагональном виде, и тогда диагональные элементы будут главными моментами инерции тела. Уравнение эллипсоида инерции тогда запишется как:

При этом координатные оси эллипсоида должны совпадать с главными осями тела.

Знание эллипсоида инерции позволяет найти момент инерции тела относительно любой оси, если только она проходит через центр эллипсоида. Для этого вдоль выбранной оси проводится радиус-вектор до пересечения с эллипсоидом инерции. Момент инерции тела относительно этой оси дается формулой: , где r - длина радиус-вектора.

9. Кинетический момент механической системы относительно центра и оси. Теорема об изменении кинетического момента механической системы.

Момент количества движения материально точки:

h - плечо

Кинетический момент или главный момент количества движения механической системы, состоящей их n точек относительно выбранного центра О равен геометрической сумме векторов моментов количества движения всех точек системы относительно этого центра:

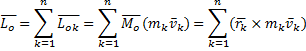
Кинетический момент системы состоящей из n точек, относительно оси равен алгебраической сумме векторов кинетических моментов всех точек системы относительно этой оси:

Теорема об изменении кинетического момента механической системы.

Производная по времени от кинетического момента механической системы относительно некоторого центра (оси) равна главному моменту внешних сил , действующих на систему , относительно этого же центра (оси).

10. Кинетический момент вращающегося тела относительно оси вращения. Вывод дифференциального уравнения вращательного движения.

Кинетический момент материальной точки относительно оси:

Если система материальных точек представляет собой абсолютно твёрдое тело, вращающееся вокруг оси, то скорость каждой точки может быть определена как v=ωh, тогда кинетический момент тела относительно оси:

Осевой момент инерции тела:

Тогда кинетический момент вращающегося тела относительно оси вращения:

Кинетический момент вращающегося тела равен произведению угловой скорости на момент инерции относительно оси вращения.

Дифференциальное уравнение вращательного движения:

11. Теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс. Дифференциальное уравнение плоскопараллельного движения твёрдого тела.

Для осей движущихся поступательно вместе с центром масс, теорема об изменении кинетического момента относительно центра масс, сохраняет тот же вид, что и относительно неподвижного центра.

Диф.ур. для плоскопараллельного движения:

12. Мощность и работа силы. Различные формулы для их вычисления.

Мощность:

Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.

,

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

P=F*v=F*v*cosa F- сила v-скорость a-угол между вектором скорости и силы

Мощность при вращательном движении: P=Mω=πMn/30

M-момент силы ω-угловая скорость n-число оборотов в минуту

Работа:

Работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы.

Работа силы - количественная мера превращения механического движения в другие виды движения.

Элементарная работа силы – это работа на бесконечно малом перемещении точки приложения силы:

δA=F ds cosϕ

Работа силы на конечном перемещении равна сумме элементарных работ:

Работа постоянной силы: A=Fs cosϕ

Работа переменной силы зависящей от перемещения:

Работа силы тяжести: A=±mgh

h-величина вертикального перемещения.

Работа сил упругости:

X1- конечная деформация пружины X0-начальная деформация пружины

Работа постоянной силы приложенной к вращающемуся телу:

Работа пары сил с моментом: M=const A=Mϕ

Работа пары сил с моментом, зависящим от угла поворота:

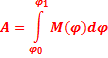
Работа силы положительна , если направление действия силы совпадает с направлением перемещения.

13. Работа силы тяжести и упругости.

Работа силы тяжести численно равна произведению силы тяжести на вертикальное перемещение точки ее приложения, не зависит от траектории перемещения, а только от расстояние между вертикальными проекциями начального и конечного положения точки:

Работа силы упругости численно равна произведению половины коэффициента жесткости на квадрат перемещения точки приложения силы, поскольку модуль силы упругости равен произведению коэффициента жесткости на удлинение:

.

14. Мощность и работа сил при поступательном и вращательном движении твёрдого тела.

Мощность при вращательном движении: P=Mω=πMn/30

M-момент силы ω-угловая скорость n-число оборотов в минуту

Работа постоянной силы приложенной к вращающемуся телу:

Работа пары сил с моментом: M=const A=Mϕ

Работа пары сил с моментом, зависящим от угла поворота:

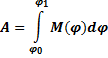
При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

15. Кинетическая энергия материальной точки и механической системы.

Теорема Кенига.

Кинетическая энергия материальной точки – скалярная положительная величина равная половине произведения массы точки на квадрат её скорости:

, [Дж], [Н·м]

Кинетическая энергия механической системы определяется как алгебраическая сумма кинетических энергий всех точек, образующих эту систему:

Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.

Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где T — полная кинетическая энергия, T₀ — энергия движения центра масс, T_r — относительная кинетическая энергия.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.

16. Кинетическая энергия механической системы. Кинетическая энергия твёрдого тела при различных движениях.

Кинетическая энергия механической системы определяется как алгебраическая сумма кинетических энергий всех точек, образующих эту систему: