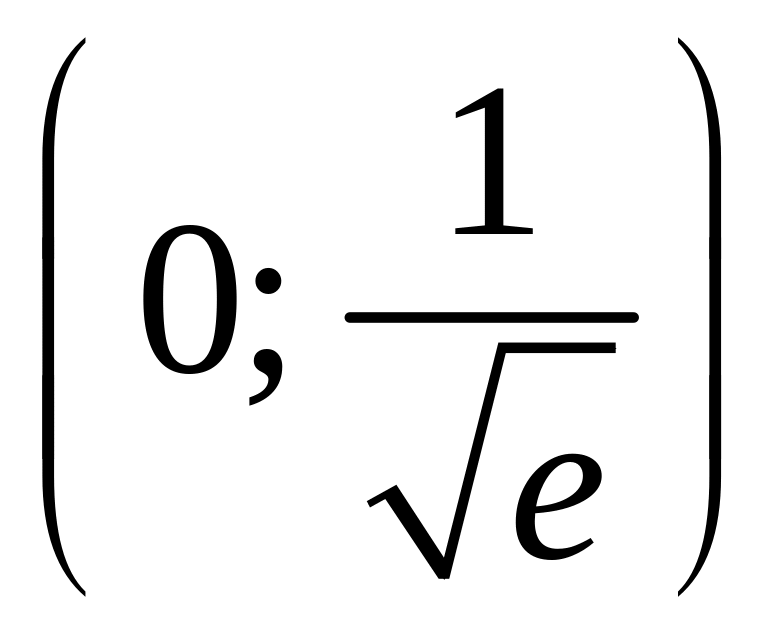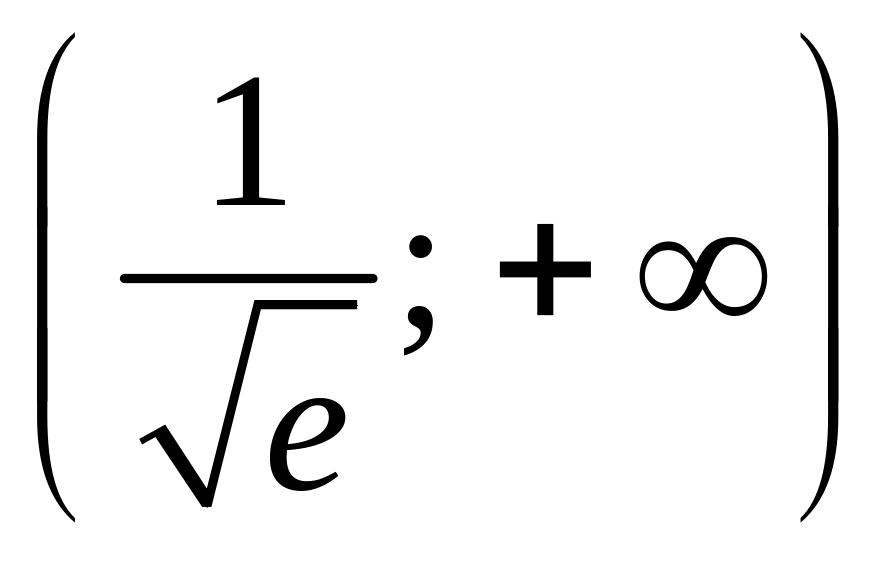- •Приложения производных
- •Задачи для самостоятельного решения
- •1.24. Уравнение касательной . Уравнение нормали . Графическая иллюстрация (рис.18).
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Формула Тейлора
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Вычислить предел функции с использованием правила Лопиталя.
1.27. ![]()
1.28. ![]()
Ответы
1.27.
![]() .
.
1.28.
![]() .
.
Формула Тейлора
Если функция
имеет непрерывные производные до
(n + 1)-го порядка включительно
в некоторой окрестности
![]() точки
,
то для всякого х из этой окрестности
справедлива формула Тейлора
точки
,
то для всякого х из этой окрестности
справедлива формула Тейлора
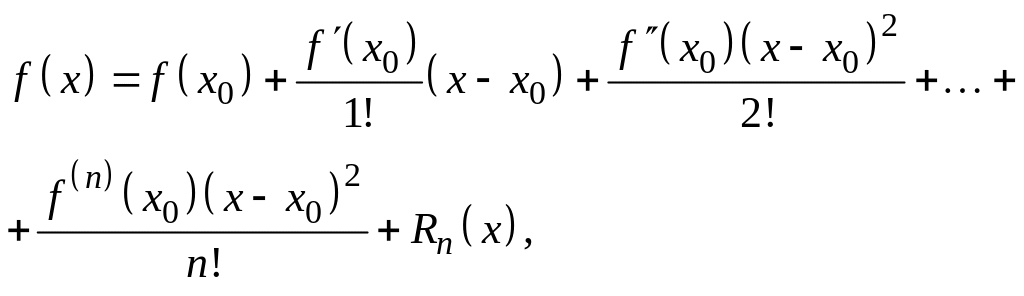
где остаточный
член
![]() в форме Лагранжа имеет вид:
в форме Лагранжа имеет вид:
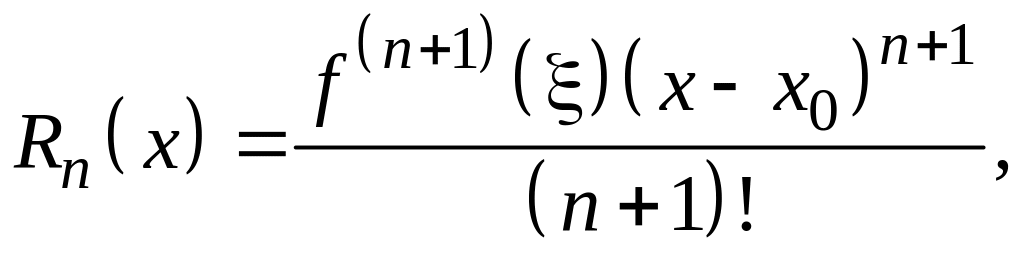
![]() или
или
![]()
Как видно, формула Тейлора позволяет представить функцию в виде суммы многочлена n-й степени и остаточного члена. Если то получается формула Маклорена
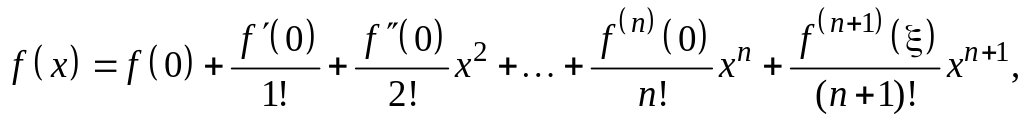
где или
Формула Тейлора используется для вычисления значений функции с заданной степенью точности и пределов функции, для доказательства достаточных условий экстремума и выпуклости (вогнутости) графика функции, используемых при исследовании функций.
Приведем разложения основных элементарных функций по формуле Маклорена:
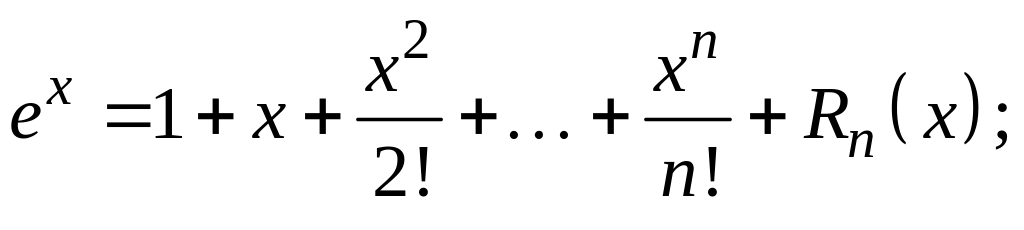
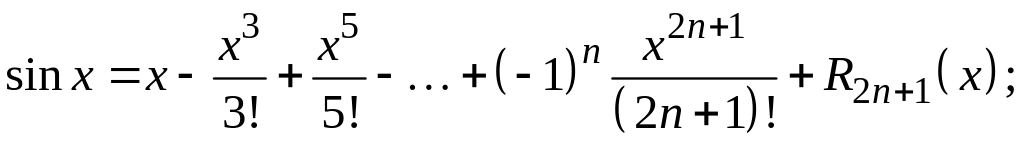
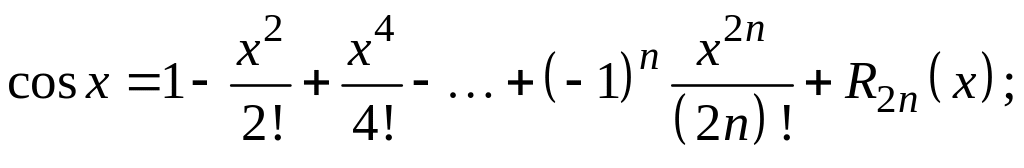
![]()
![]()

Рассмотрим задание:
разложить функции в ряд Тейлора по
степеням
![]() до члена
до члена
![]() включительно.
включительно.
Приведем решение примера.
Пример 1.46.
![]()
Решение.
Первый способ. Разложим линейную
функцию
![]() Это многочлен
первого порядка. Его разложение имеет
вид
Это многочлен
первого порядка. Его разложение имеет
вид
![]() так
как
так
как
![]() остальные производные равны нулю.
Разложим функцию
остальные производные равны нулю.
Разложим функцию
![]() Найдем
Найдем
![]()
![]() ,
следовательно,
,
следовательно,
![]() и
и
![]() Согласно формуле Тейлора искомое
разложение имеет вид:
Согласно формуле Тейлора искомое
разложение имеет вид:
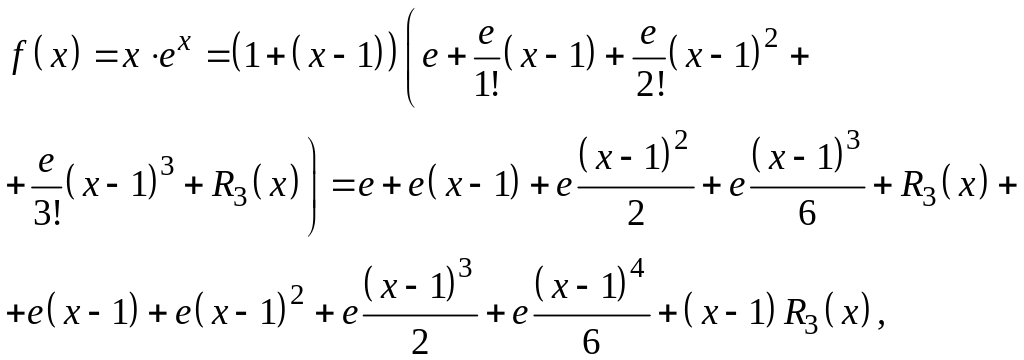
где
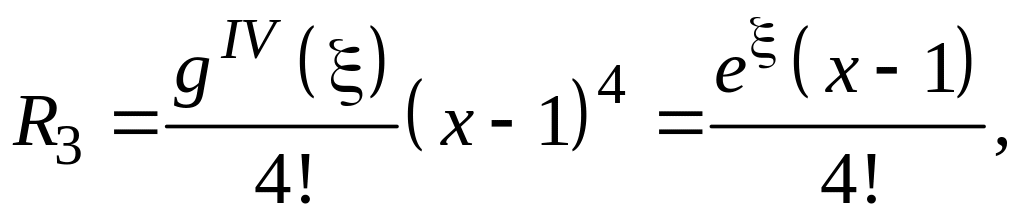
![]() при х > 1 или
при х > 1 или
![]() при х < 1.
при х < 1.
Величины
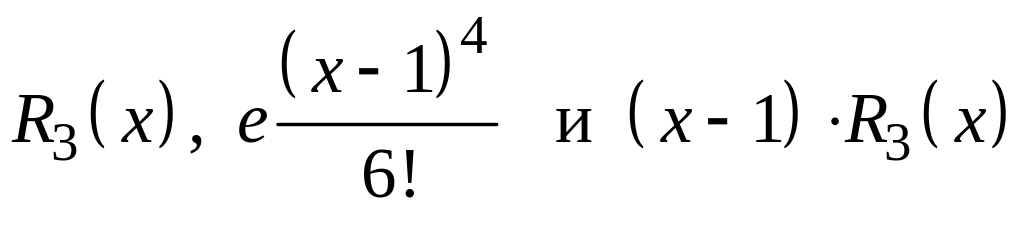 содержат
содержат
![]() в четвертой и пятой степени. Их сумму
можно объединить в остаточный член
в четвертой и пятой степени. Их сумму
можно объединить в остаточный член
![]() т.е.
т.е.
 тогда
окончательно получим:
тогда
окончательно получим:
![]()
Второй способ.
Найдем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Согласно формуле Тейлора
Согласно формуле Тейлора
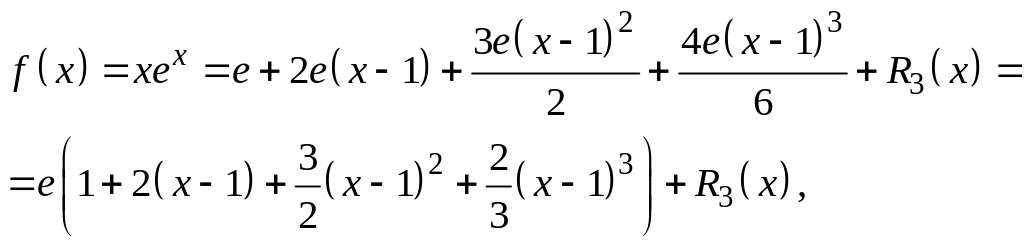
где остаточный
член
 при х > 1 или
при х < 1.
при х > 1 или
при х < 1.
Задачи для самостоятельного решения
Разложить функцию в ряд Тейлора по степеням до члена включительно.
1.29. ![]()
1.30. ![]()
Ответы
1.29.
![]() .
.
1.30.
![]() .
.
Исследование функций и построение графиков
Общая схема исследования функции и построения графика может быть укрупнённо разбита на три части (этапы исследования).
Первый этап - этап использования свойств самой функции. В него входят:
1) нахождение области определения функции;
2) нахождение нулей (корней) функции (точек пересечения графика функции с осью абсцисс), если эти корни возможно вычислить точно или приближенно;
3) проверка функции на четность или нечетность;
4) проверка непрерывности, нахождение и классификация точек разрыва в случае нарушения непрерывности;
5) вычисление пределов функции на границах области определения.
Второй этап - этап использования первой производной. Он включает:
6) вычисление первой производной;
7) нахождение критических точек;
8) нахождение точек экстремума;
9) определение промежутков возрастания и убывания.
Критическими точками функции называются внутренние точки области определения, в которых производная равна нулю или не существует.
Точками экстремума функции называются точки максимума или минимума.
Точка
называется точкой максимума, если
существует ее окрестность
![]() такая, что для любых
такая, что для любых
![]() выполняется неравенство
выполняется неравенство
![]() Аналогично, точка
называется точкой минимума, если
существует ее окрестность
Аналогично, точка
называется точкой минимума, если
существует ее окрестность
![]() такая, что для любых
выполняется неравенство
такая, что для любых
выполняется неравенство
![]()
Согласно необходимому условию экстремума (теорема Ферма) точки экстремума следует искать только среди критических точек. Критическая точка только тогда будет точкой экстремума, если для нее выполняется одно из достаточных условий экстремума.
Первое достаточное условие экстремума функции.
Теорема.
Пусть в
некоторой выколотой окрестности
![]() критической точки
существует конечная производная
критической точки
существует конечная производная
![]() и как слева от
так и справа от
сохраняет знак, тогда:
и как слева от
так и справа от
сохраняет знак, тогда:
1) если
![]() при
при
![]() и
и
![]() при
при
![]() ,
то в точке
функция
имеет максимум;
,
то в точке
функция
имеет максимум;
2) если при и при , то в точке функция имеет минимум;
3) если не меняет знак при переходе через точку , то экстремума в точке нет.
Доказательство
теоремы основано на следствии из теоремы
Лагранжа, а именно: если
имеет на промежутке
![]() производную
для любого
производную
для любого
![]() из
,
то
на
монотонно возрастает; если
для любого
из
,
то функция
на
монотонно убывает.
из
,
то
на
монотонно возрастает; если
для любого
из
,
то функция
на
монотонно убывает.
Второе достаточное условие экстремума.
Теорема. Пусть
имеет первую производную
в окрестности
критической точки
и вторую производную
![]() в самой точке
.
Если
в самой точке
.
Если
![]() то точка
- точка минимума; если
то точка
- точка минимума; если
![]() то точка
- точка максимума; если же
то точка
- точка максимума; если же
![]() то нужны дополнительные исследования
с привлечением высших производных.
то нужны дополнительные исследования
с привлечением высших производных.
Второе достаточное
условие экстремума имеет более узкий
круг применения, так как оно неприменимо
к тем критическим точкам
,
где не существует конечной первой
производной, и в случае, когда
![]()
Третий этап - этап использования второй производной и нахождения асимптот. В него входят:
10) вычисление второй производной;
11) нахождение точек перегиба, промежутков выпуклости и вогнутости функции;
12) нахождение вертикальных и наклонных асимптот.
Функция называется выпуклой кверху в точке , если существует окрестность такая, что для всех график функции лежит ниже касательной к графику в точке .
Функция называется выпуклой книзу в точке , если существует окрестность такая, что для всех график функции лежит выше касательной к графику в точке .
Точка
![]() графика функции называется точкой
перегиба,
если она отделяет участок кривой, где
выпукла кверху, от участка кривой, где
выпукла книзу. Абсциссы точек перегиба
следует искать из уравнения
графика функции называется точкой
перегиба,
если она отделяет участок кривой, где
выпукла кверху, от участка кривой, где
выпукла книзу. Абсциссы точек перегиба
следует искать из уравнения
![]() (необходимое условие наличия точки
перегиба). Корни этого уравнения только
тогда будут абсциссами точек перегиба,
если для них выполняется достаточное
условие точки перегиба, приведенное в
следующей теореме.
(необходимое условие наличия точки
перегиба). Корни этого уравнения только
тогда будут абсциссами точек перегиба,
если для них выполняется достаточное
условие точки перегиба, приведенное в
следующей теореме.
Теорема. Пусть
существует
![]() на промежутке
.
Тогда, если при переходе через точку
меняет знак, то
- абсцисса точки перегиба; если
не меняет знак, то перегиба нет.
на промежутке
.
Тогда, если при переходе через точку
меняет знак, то
- абсцисса точки перегиба; если
не меняет знак, то перегиба нет.
Определение.
Прямая
![]() является вертикальной асимптотой
графика функции f(x), если хотя
бы один из пределов
является вертикальной асимптотой
графика функции f(x), если хотя
бы один из пределов
![]() или
или
![]() равен бесконечности.
равен бесконечности.
Определение.
Если функция f(x) задана для x > M
(x < M), то прямая Y = kx + b
является наклонной асимптотой графика
функции f(x) при
![]() если f(x) = kx + b + (x),
где
если f(x) = kx + b + (x),
где
![]()
На графике асимптота изображается прямой, к которой неограниченно близко приближаются значения функции (не сливаясь с ней).
Вертикальные
асимптоты функции существуют, если
находятся конечные точки
такие, что
![]() Для определения правых и левых наклонных
асимптот необходимо и достаточно
вычислить четыре предела и показать,
что они конечны:
Для определения правых и левых наклонных
асимптот необходимо и достаточно
вычислить четыре предела и показать,
что они конечны:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
Если хотя бы один из пределов не существует или бесконечен, то соответствующей наклонной асимптоты нет. В противном случае уравнения асимптот имеют вид:
![]() - правая асимптота;
- правая асимптота;
![]() - левая асимптота.
- левая асимптота.
Если K1 = K2, b1 = b2, то правая асимптота совпадает с левой.
Горизонтальная
асимптота является частным случаем
наклонной
![]()
После проведенных исследований строится график функции. Для уточнения кривой берется небольшое (порядка пяти) количество точек оси абсцисс (из области определения) и вычисляются значения в этих точках.
Рассмотрим примеры.
Пример
1.47. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
Решение. Начнем с первого этапа.
1. Область определения
![]()
2. Нули функции. Приравняем к нулю:
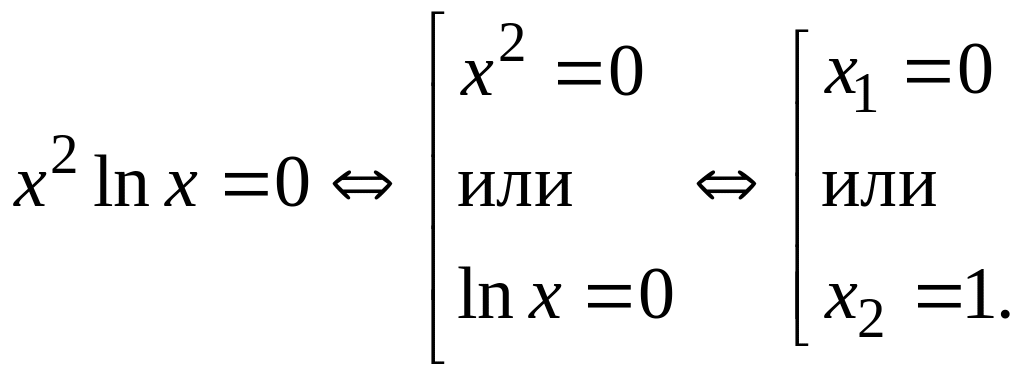
Первый корень не
годится, так как не входит в
![]() Итак, график
пересекает ось абсцисс в точке
Итак, график
пересекает ось абсцисс в точке
![]()
3. Четность
(нечетность) функции
не является ни четной, ни нечетной
функцией, так как определена только при
![]() следовательно, график
не будет симметричен ни относительно
оси ординат, ни относительно начала
координат.
следовательно, график
не будет симметричен ни относительно
оси ординат, ни относительно начала
координат.
4. Непрерывность.
Функция
![]() непрерывна в области определения как
произведение двух непрерывных функций
непрерывна в области определения как
произведение двух непрерывных функций
![]() Вычислим ее предел при
Вычислим ее предел при
![]() :
:
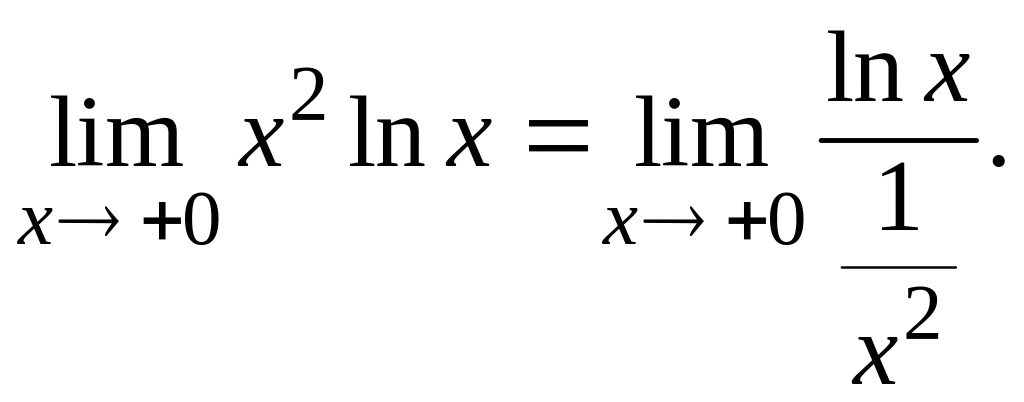 Можно применить правило Лопиталя для
раскрытия неопределенности типа
:
Можно применить правило Лопиталя для
раскрытия неопределенности типа
:
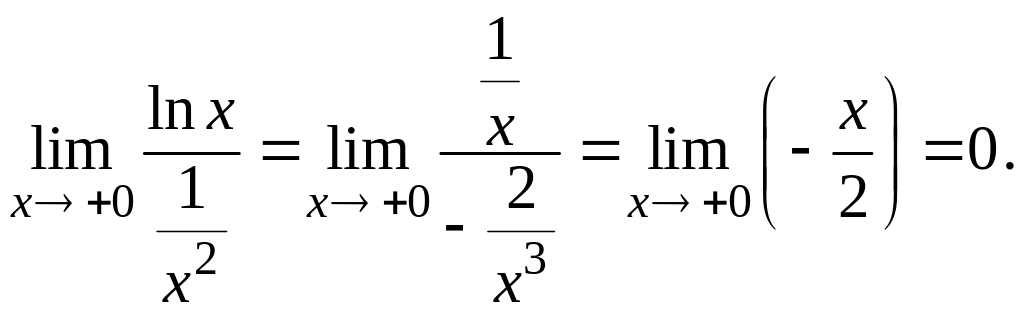
5. Вычислим предел
при
![]() он очевиден:
он очевиден:
![]()
Перейдем ко второму этапу.
6. Найдем первую производную:
![]()
7. Приравняем
к нулю и найдем критические точки, решив
уравнение
![]() не годится, так как 0 не входит в область
определения функции;
не годится, так как 0 не входит в область
определения функции;
![]()
![]()
![]()
8. Определим точку экстремума. Составим таблицу:
X |
|
|
|
|
– |
0 |
+ |
|
|
|
|
В первую строку занесем интервалы, на которые область определения функции разбивается критическими точками, и сами точки. В рассматриваемом примере критическая точка одна, а интервалов два.
Во вторую строку запишем знак производной на каждом интервале, полученный непосредственной проверкой (подстановкой любого значения х из рассматриваемого интервала в выражение для производной).
Далее вычислим значение функции в точке экстремума (минимума)
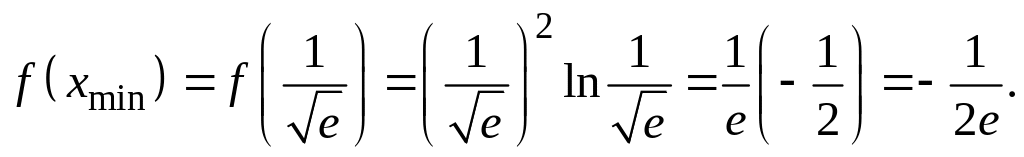
В третью строку запишем символы возрастания
( ) и убывания
( ) и установленное
значение экстремума.
третью строку запишем символы возрастания
( ) и убывания
( ) и установленное
значение экстремума.
9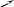 .
По таблице определим промежутки
возрастания
.
По таблице определим промежутки
возрастания
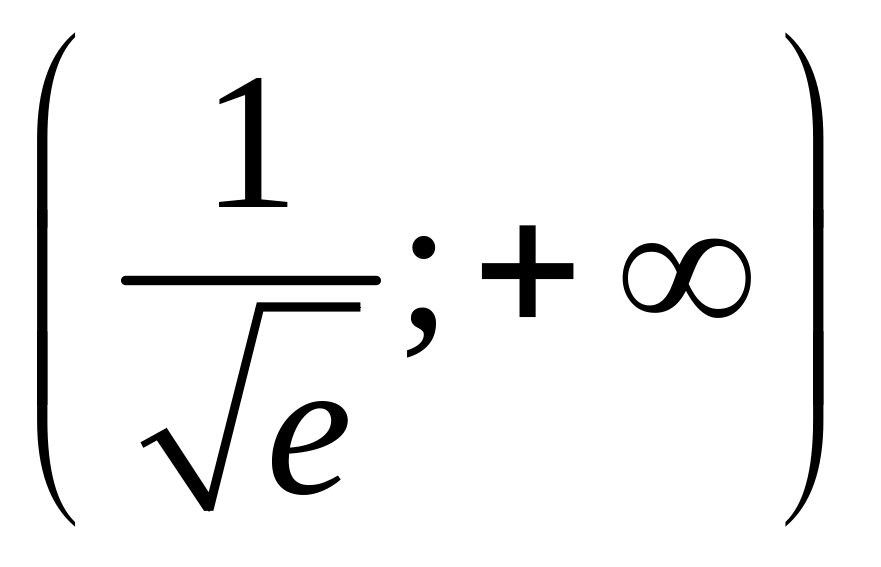 и убывания
и убывания
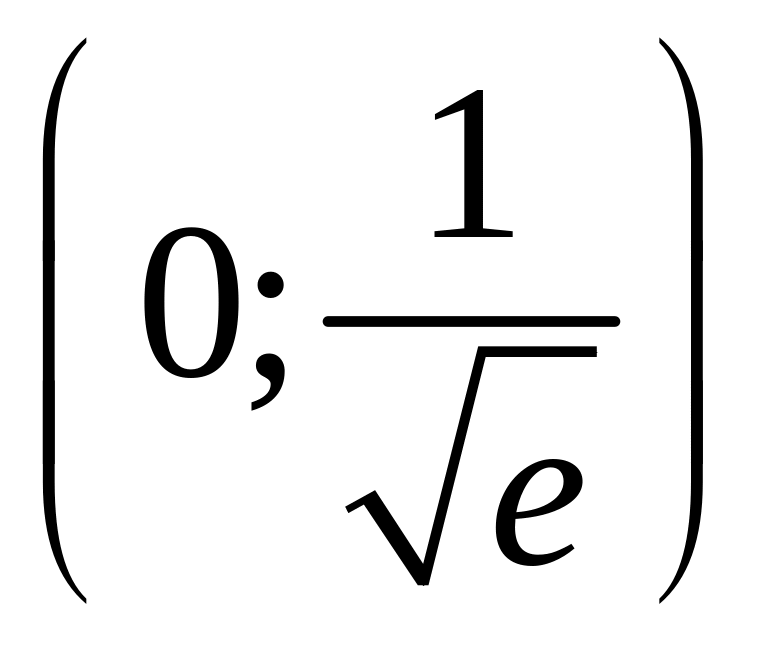 функции.
функции.
Перейдем к третьему этапу.
10. Вычислим вторую производную:
![]()
11. Приравняем к нулю, определим возможные абсциссы точек перегиба:
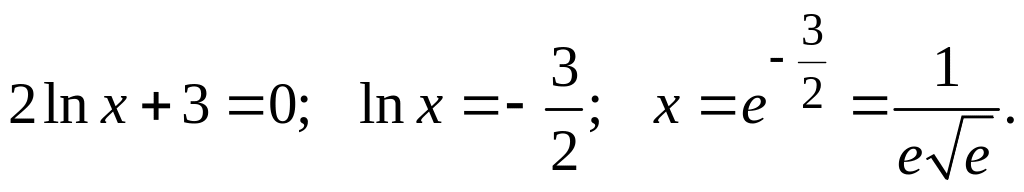
С
x
–
0
+
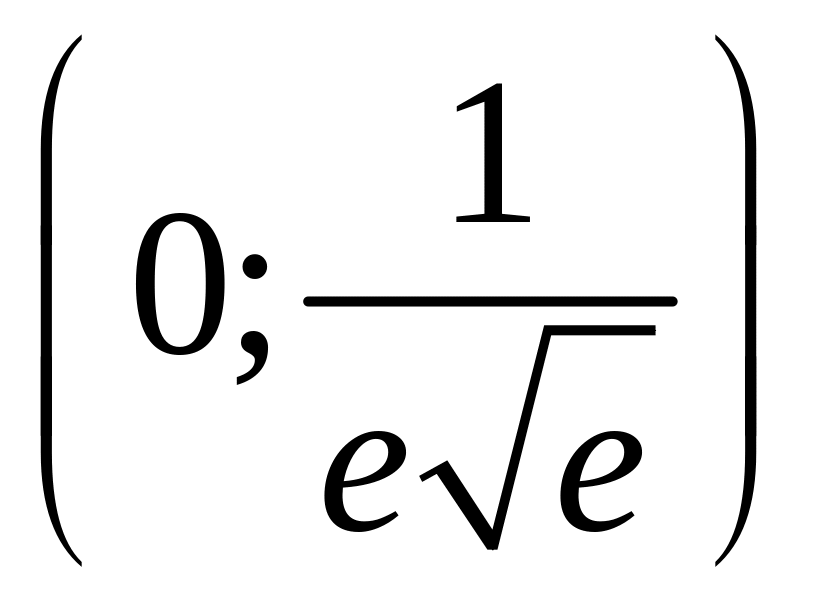
![]()

![]()
В верхнюю строку запишем интервалы, на которые область определения функции разбивается предполагаемыми абсциссами точек перегиба, и сами абсциссы. В рассматриваемом примере предполагаемая точка перегиба одна, а интервалов два.
Во вторую строку запишем знак второй производной в каждом интервале, полученный непосредственной подстановкой любого значения х из рассматриваемого интервала.
В третью строку занесем символы (функция выпукла книзу) и (функция выпукла кверху).
Так как слева от
значения
![]() (входящего в область определения функции)
f(x) выпукла, а справа - вогнута,
указанное значение является абсциссой
точки перегиба. Ордината точки перегиба
(входящего в область определения функции)
f(x) выпукла, а справа - вогнута,
указанное значение является абсциссой
точки перегиба. Ордината точки перегиба
![]()
Рассмотрим последний пункт третьего этапа.
12. У рассматриваемой
функции нет вертикальных асимптот, так
как нет точек разрыва. Проверим наличие
наклонной. Вычислим первый предел:
![]() Значит, наклонной асимптоты тоже нет.
Значит, наклонной асимптоты тоже нет.
На этом исследование функции полностью завершено. Принципиальное поведение кривой известно. Для уточнения положения кривой вычислим значения функций в конечном числе вспомогательных точек (пять - десять). Построение графика начнем с нанесения на оси координат точек экстремума, перегиба и корня функции. Далее нанесем координаты вспомогательных точек. Построим кривую по точкам.
П

![]() (рис.19).
(рис.19).
Дополнительно
можно рассмотреть предел производной
при
![]()
![]() (по правилу Лопиталя). Следовательно,
при
график функции приближается к оси
абсцисс как к своей касательной.
(по правилу Лопиталя). Следовательно,
при
график функции приближается к оси
абсцисс как к своей касательной.
Пример 1.48.
Исследовать и построить график функции
![]()
Решение. Начнем с первого этапа.
1. Область определения
![]()
2. Нули функции.
Приравняем
к нулю:
![]() .
Действительных корней нет, следовательно,
график не пересекает ось абсцисс.
.
Действительных корней нет, следовательно,
график не пересекает ось абсцисс.
3. Четность (нечетность) функции. Проверим функцию на четность (нечетность):
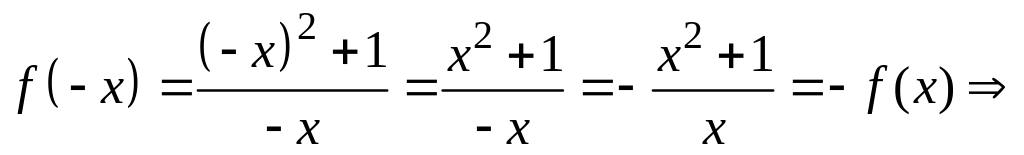
- функция нечетная, поэтому график будет симметричен относительно начала координат.
4.
Непрерывность. Функция не определена
в точке х = 0,
следовательно, не является непрерывной
в этой точке. В остальных точках области
определения функция непрерывна. Определим
вид точки разрыва. Найдем предел:
![]() Числитель стремится к единице, а
знаменатель - к нулю, оставаясь
отрицательным. Следовательно,
Числитель стремится к единице, а
знаменатель - к нулю, оставаясь
отрицательным. Следовательно,
![]() Аналогично,
Аналогично,
![]() Итак, точка х = 0
является точкой разрыва второго рода.
Итак, точка х = 0
является точкой разрыва второго рода.
5. Пределы функции на границах области определения равны:
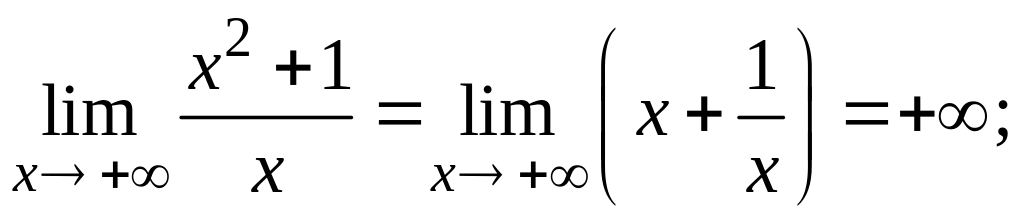
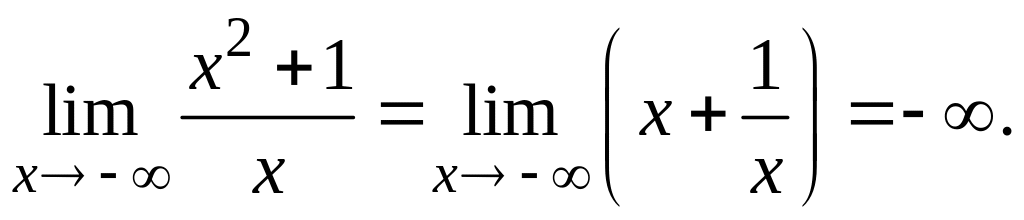
Перейдем ко второму этапу.
6. Вычислим первую производную:
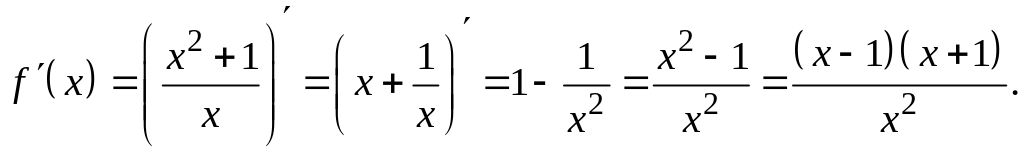
7. Приравняем
к нулю:
![]()
![]() Имеем две критические точки
Имеем две критические точки
![]()
8. Определим точки экстремума. Составим таблицу (точки, в которых производная не существует, обязательно включаются в таблицу):
x |
|
–1 |
(–1; 0) |
0 |
(0; 1) |
1 |
|
|
+ |
0 |
– |
Не существует |
– |
0 |
+ |
|
|
max = = –2 |
|
Не существует |
|
min = = 2 |
|
В верхнюю строку занесем интервалы, на которые область определения функции разбивается критическими точками, и сами точки. В рассматриваемом примере критических точек две, а интервалов четыре.
Найдем значения в точках экстремума:
![]()
9. Функция возрастает
на промежутках
![]() и
и
![]() ,
а убывает на промежутках
,
а убывает на промежутках
![]() и
и
![]() .
.
Перейдем к третьему этапу.
10. Вычислим вторую производную:
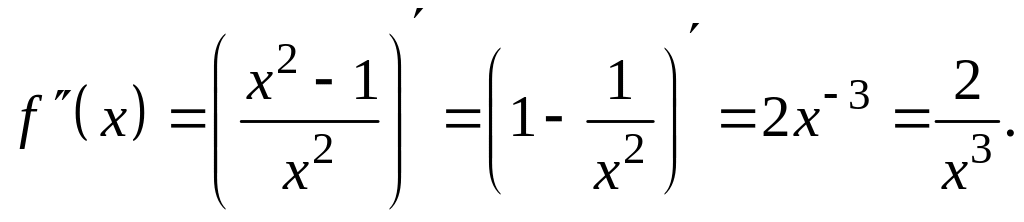
11. Вторая производная не обращается в нуль, но в точке х = 0 не определена. Значит, точек перегиба у нее нет.
С
x
0
–
Не
существует
+
Не
существует
![]()
![]()
На интервале выпукла кверху, на интервале выпукла книзу.
12. У рассматриваемой функции есть вертикальная асимптота х = 0 (см. п. 4).
Найдем наклонную асимптоту:
1)
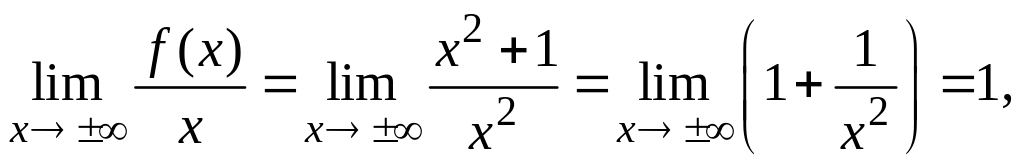 значит,
значит,
![]()
![]() ;
;
2)

![]() значит, b = 0.
значит, b = 0.
Итак, уравнение
наклонной асимптоты имеет вид:
![]()
П
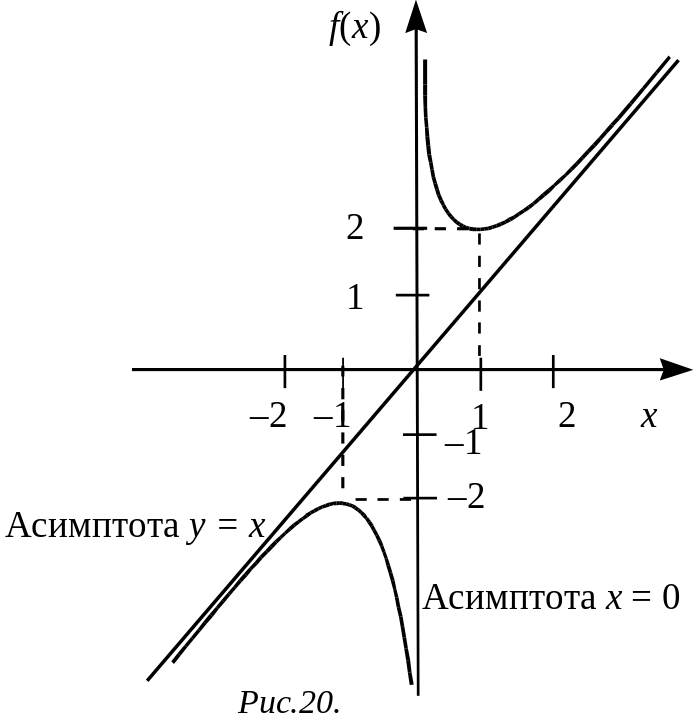
![]() (рис.20).
(рис.20).