2.Парадокс в операции умножения (доказательство №2)

“ И измерил он город тростью на 12 тысяч стадий… И стену его измерил во 144 локтя, мерой человеческою, какова мера и

Ангела” (Апокалипсис, 23,2-17)

Линейный натуральный ряд чисел является лишь частным случаем в общей совокупности: линейность+нелинейности. Тогда, при переходе на любой иной ряд чисел, мы неминуемо придем именно к какой-то нелинейности. Родоначальники нашей пра-цивилизации Шумера, о чем говорят библейские и другие источники, пользовались не только нелинейной полуквадратичной шкалой чисел, но и 60-ричной системой счисления. Это позволяло им, наряду с использованием другого базового числа – 12, решать задачи на сфере с помощью прямоугольного треугольника, определять точку на поверхности сферы всего одной координатой, с помощью -параметра характеризовать окружающее пространство, использовать непрерывную логику, имеющей в отличие от нашей двоично-дискретной, неограниченное количество градаций между понятиями “да” и “нет” и т.д.

Известно, что координаты точек, определенные в одной системе координат, непременно должны пересчитываться в любую другую. То же самое можно сказать и о различных системах счисления. Как логическое следствие, мы вправе ожидать наличие связей между различными шкалами чисел.

На графике 1 показана связь натуральной и полуквадратичной (шумерской) шкал чисел. Здесь ось ординат (функция f(k)) – ось натуральных чисел, а ось абсцисс (аргумент k) – ряда новых чисел. Синяя линия графика – ни что иное, как график используемой нами квадратичной функции.

Но, тут же видим несуразность: при переходе от шумерской полушкалы отрицательных чисел мы не получим отрицательных чисел линейной шкалы! Они начисто отсутствуют!

Выход один: понять, что наши предки использовали другую интерпретацию квадратичной шкалы, вид которой показан на графике красной линией. Тогда все становится на свои места: возведя в квадрат шумерское число “–12”, получим наше натуральное число “-144” и наоборот, а наши предыдущие рассуждения, доводы и выводы - получат новое подтверждение.

Так как умножение чисел является одной из основополагающих математических операций, то и последствия ее изменения будут всеобъемлющими. Понятно, что переработка накопленных знаний одному человеку не под силу, заметим, например, что изменится суть операции логарифмирования. Левая (отрицательная) часть характеристики логарифмов числа будет зеркальным отражением ее правой части и размещаться в 3-м квадранте с тем, что -ln(-x)=ln(x). Нулевая точка этой характеристики так же, как и в классическом варианте, не будет иметь смысла.

Нововведения, например, захватят суть тригонометрических функций прямоугольника [tg(α), ctg(α), соотношения sin²(α)+cos²(α)=1 – для 2,3 и 4 квадрантов и т.п.], а также напрямую коснутся результатов решения различных уравнений. Как подтверждение, рассмотрим эти последствия для уравнений 2-й и 3-й степени.

3. Р ешение уравнений 2-й степени в примерах

А.Классическая методика

1. Уравнение x²+2x-8=0 имеет два действительных корня (x₁=-4) и (x₂=2)

Примечание: здесь и далее уравнения решаются графическим способом, когда исходное уравнение разбивается на 2 других. Причем в качестве 2-го используется уравнение прямой, соответствующей значению свободного члена исходного уравнения.

2. Уравнение x²-4x+13=0 действительных корней не имеет

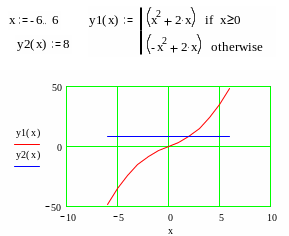
Б.Новая методика (в сравнении)

1. Уравнение x²+2x-8=0 имеет 1 решение (x=2)

2. Уравнение x²-4x+13=0 имеет 1 решение (x₁≈-8.525), но при другом свободном члене может иметь 1, 2 или 3 решения

4. Решение уравнений 3-й степени в примерах

А .Классическая методика

Уравнение x³-6x²+21x-26=0 имеет 1 действительный корень (x=2) и может быть представлено как (x-2)(x-2-3i)(x-2+3i)=0

Б .Новая методика (в сравнении)

Уравнение x³-6x²+21x-26=0 имеет 1 решение (x=2), совпадающее с действительным классическим

Приведенные примеры новой методики и дополнительные проработки показывают:

• каждое уравнение 2-й или 3-й степени обязательно имеет 1 решение, представленное действительным числом;

• количество решений в уравнениях 2-й степени может достигать 3-х, а в уравнениях 3-й степени – 5-ти.

На этих примерах можно убедиться – каких кардинальных изменений потребует вся математика, по сравнению с которыми меркнет по значимости уход ее целого пласта – мнимых чисел, либо, применительно к числам, - исключение термина “действительные”.