Пример. В результате эксперимента получены следующие статистические данные (табл.2.1):
Таблица 2.1
x |
y |
x |
y |
x |
y |
x |
y |
x |
y |
8,35 |
3,50 |
10,50 |
6,00 |
11,35 |
9,50 |
12,15 |
6,00 |
12,85 |
9,50 |
8,74 |
1,49 |
10,75 |
2,50 |
11,50 |
6,00 |
12,25 |
8,05 |
13,15 |
9,02 |
9,25 |
6,40 |
10,76 |
5,74 |
11,50 |
9,00 |
12,35 |
5,01 |
13,25 |
6,49 |
9,50 |
4,50 |
11,00 |
8,50 |
11,62 |
8,50 |
12,50 |
7,03 |
13,26 |
10,50 |
9,75 |
5,00 |
11,00 |
5,26 |
11,75 |
10,00 |
12,76 |
7,53 |
13,40 |
7,51 |
10,24 |
7,00 |
11,25 |
8,00 |
12,00 |
9,00 |
12,85 |
6,01 |
13,50 |
10,00 |
13,65 |
9,50 |
14,50 |
10,00 |
13,75 |
8,51 |
14,75 |
12,00 |
14,00 |
11,00 |
15,25 |
12,50 |
14,23 |
8,40 |
16,00 |
11,50 |
14,26 |
10,00 |
16,00 |
13,00 |
14,51 |
9,50 |
16,25 |
12,00 |
|
|
|
|
|
|
Для приведенной выборки выполнить следующие задания.
1) Представить выборку в виде интервальных статистических рядов по случайным величинам X и Y.
2) Для случайной
величины X
построить полигон частот и гистограмму.
Найти эмпирическую функцию распределения
и построить ее график.
3) Найти выборочные числовые характеристики (выборочное среднее, несмещенную выборочную дисперсию, несмещенное среднее квадратичное отклонение) для случайных величин X и Y.
4) Построить доверительные интервалы для математического ожидания и дисперсии для случайной величины X с доверительной вероятностью β=0,95.
5) Проверить гипотезу о нормальном распределении случайной величины X.
6) Провести корреляционный анализ.
7) Построить линейную регрессионную модель.
Решение. Объем выборки равен n=42.
1. Для представления выборки в виде интервальных статистических рядов определяем длины интервалов для каждой случайной величины.
Для случайной величины X наибольшим значением является 16,25, наименьшим – 8,35. Найдем длину интервала по X:
Выбираем hx=1,2. Получаем семь интервалов. От наименьшего значения 8,35 отступим немного левее, таким образом, первый интервал начнем со значения 8,3. Подсчитаем частоту попадания случайной величины X в каждый интервал, причем условимся, что граничное значение будет входить в больший интервал. Интервальный статистический ряд для X принимает вид (табл.2.2):
Таблица 2.2
Грани-цы интер-валов |
8,3–9,5 |
9,5–10,7 |
10,7–11,9 |
11,9–13,1 |
13,1–14,3 |
14,3–15,5 |
15,5–16,7 |
|
3 |
4 |
10 |
8 |
10 |
3 |
4 |
Для случайной величины Y наибольшим значением является 13,0, наименьшим – 1,49. Найдем длину интервала по Y:
Выбираем hy=1,8. Получаем семь интервалов. От наименьшего значения 1,49 отступим немного левее, таким образом, первый интервал начнем со значения 1,5. Подсчитаем частоту попадания случайной величины Y в каждый интервал, причем условимся, что граничное значение будет входить в больший интервал. Интервальный статистический ряд для Y принимает вид (табл.2.3):
Таблица 2.3
Грани-цы интер-валов |
1,5–3,3 |
3,3–5,1 |
5,1–6,9 |
6,9–8,7 |
8,7–10,5 |
10,5–12,3 |
12,3–14,1 |
|
2 |
4 |
8 |
11 |
10 |
4 |
3 |
2. Чтобы построить полигон частот для случайной величины X, найдем середину и относительную частоту для каждого интервала (табл.2.4).
Таблица 2.4
Границы интервалов |
8,3–9,5 |
9,5–10,7 |
10,7–11,9 |
11,9–13,1 |
13,1–14,3 |
14,3–15,5 |
15,5–16,7 |
Середины интервалов
|
8,9 |
10,1 |
11,3 |
12,5 |
13,7 |
14,9 |
16,1 |
|
3 |
4 |
10 |
8 |
10 |
3 |
4 |
|
|
|
|
|
|
|
|
На рис.2.1 по оси
абсцисс отмечаем середины интервалов
xi,
по оси ординат – относительные частоты
.
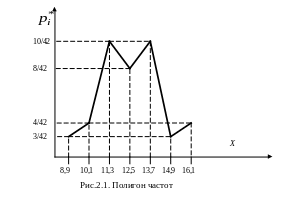
При построении гистограммы распределения по оси абсцисс отмечаем границы интервалов, по оси ординат – относительные частоты, деленные на длину интервала (рис.2.2).
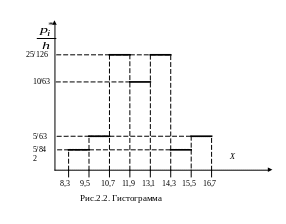
Эмпирическую функцию распределения находим по формуле:
.
Для того чтобы найти значение эмпирической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение меньше, чем х, и разделить на общее число произведенных опытов n.
Построим график эмпирической функции распределения (рис.2.3).
3. Для вычисления оценок числовых характеристик для X используем таблицу (2.5).
Таблица 2.5
Границы интервалов |
Середина интервала
|
Частота
|
|
|
8,3 – 9,5 |
8,9 |
3 |
26,7 |
237,63 |
9,5 – 10,7 |
10,1 |
4 |
40,4 |
408,04 |
10,7 – 11,9 |
11,3 |
10 |
113 |
1276,9 |
11,9 – 13,1 |
12,5 |
8 |
100 |
1250,0 |
13,1 – 14,3 |
13,7 |
10 |
137 |
1876,9 |
14,3 – 15,5 |
14,9 |
3 |
44,7 |
666,03 |
15,5 – 16,7 |
16,1 |
4 |
64,4 |
1036,84 |
Сумма |
|
42 |
526,2 |
6752,34 |
В формулу выборочного среднего подставляем сумму по четвертому столбцу (табл.2.5):
В формулу несмещенной выборочной дисперсии подставим сумму по пятому столбцу (табл.2.5):
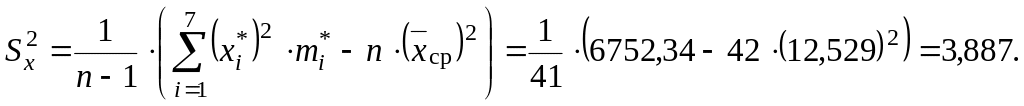Несмещенное
выборочное среднее квадратичное
отклонение:
Для вычисления оценок числовых характеристик для Y используем таблицу (2.6).
Таблица 2.6
Границы интервалов |
Середина интервала
|
Частота
|
|
|
1,5 – 3,3 |
2,4 |
2 |
4,8 |
11,52 |
3,3 – 5,1 |
4,2 |
4 |
16,8 |
70,56 |
5,1 – 6,9 |
6,0 |
8 |
48 |
288 |
6,9 – 8,7 |
7,8 |
11 |
85,8 |
669,24 |
8,7 – 10,5 |
9,6 |
10 |
96 |
921,6 |
10,5 – 12,3 |
11,4 |
4 |
45,6 |
519,84 |
12,3 – 14,1 |
13,2 |
3 |
39,6 |
522,72 |
Сумма |
|
42 |
336,6 |
3003,48 |
В формулу выборочного среднего подставляем сумму по четвертому столбцу (табл.2.6):
В формулу несмещенной выборочной дисперсии подставим сумму по пятому столбцу (табл.2.6):
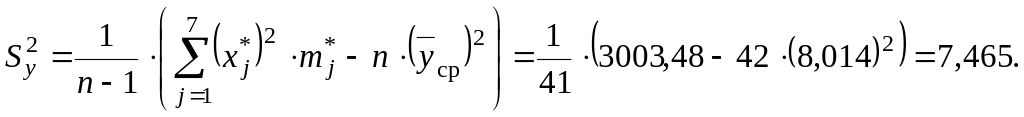
Несмещенное выборочное среднее квадратичное отклонение:
4. Построим доверительные интервалы для математического ожидания и дисперсии для случайной величины X при доверительной вероятности β=0,95.
По таблице 4 приложений находим значение статистики Стьюдента для доверительной вероятности β=0,95 и числа степеней свободы k=42-1=41:
Половина длины доверительного интервала:
Подставляем полученные значения в формулу доверительного интервала для математического ожидания:
Для определения доверительного интервала для дисперсии по таблице 3 приложений найдем значение статистики χ2 для уровня значимости α=1–β=1–0,95=0,05 и числа степеней свободы k=42-1=41:
Подставим найденные значения статистики χ2 в формулу доверительного интервала для дисперсии:
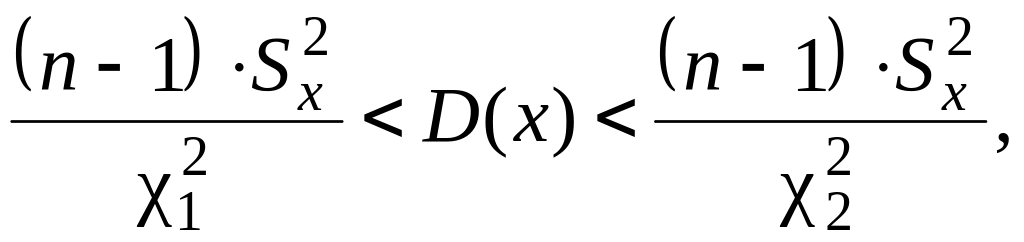
Таким образом, истинные значения математического ожидания M(x) и дисперсии D(x) попадают в полученные интервалы с вероятностью β=0,95.