
- •Кинематика Контрольные задания для выполнения расчетных и курсовых работ
- •Общие требования к оформлению расчетной работы
- •Кинематика точки
- •Краткие сведения из теории Определение положения точки
- •Определение скорости точки
- •Определение ускорения точки
- •Определение радиуса кривизны траектории точки
- •Порядок выполнения задания
- •Исходные данные
- •Вращательное движение твердого тела вокруг (около) неподвижного полюса
- •Краткие сведения из теории
- •Кинематические характеристики вращательного движения твердого тела вокруг (около) неподвижного полюса
- •Скорость и ускорение произвольной точки твердого тела, вращающегося вокруг неподвижного полюса
- •Порядок выполнения задания
- •Варианты заданий (условия задач)
- •Исходные данные
- •Рисунки к вариантам 120
- •Плоскопараллельное движение твердого тела
- •Краткие сведения из теории
- •Порядок выполнения задания
- •Исходные данные
- •Вариант 25
- •Движение точки относительно двух систем отсчета, перемещающихся одна относительно другой
- •Краткие сведения из теории
- •Порядок выполнения задания
- •Варианты заданий (условия задач)
- •Исходные данные
- •Библиографический список
- •Образец титульного листа расчетной работы
- •Расчетная работа
- •Кинематика: контрольные задания для выполнения расчетных и курсовых работ
- •190005, С.-Петербург, 1-я Красноармейская ул., д.1
Рисунки к вариантам 120
Стр. 37-41
П р и м е р. Конус 1
с углом 2
при вершине катится без скольжения (в
указанном стрелкой направлении) по
неподвижному конусу с углом 2
при вершине. Высота конуса 1
OC = h.
Движение
конуса происходит так, что осестремительное
ускорение центра С
основания
конуса
постоянно и равно
.
Исходные данные
в таблице и на рис. 2.5.
р и м е р. Конус 1
с углом 2
при вершине катится без скольжения (в
указанном стрелкой направлении) по
неподвижному конусу с углом 2
при вершине. Высота конуса 1
OC = h.
Движение
конуса происходит так, что осестремительное
ускорение центра С
основания
конуса
постоянно и равно
.
Исходные данные
в таблице и на рис. 2.5.
Рис. 2.5
Определить:
1) алгебраические
величины проекций угловых скоростей
прецессии и ротации на оси
![]() ,
и
,
и
![]() соответственно и мгновенную угловую
скорость конуса;
соответственно и мгновенную угловую
скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорение точек В и С (найти вращательное, а также нормальное и касательное ускорения точки С).
Исходные данные:
![]()
![]() 0,36
м/с2.
0,36
м/с2.
Решение.
Осестремительное
ускорение точки С
определяется по формуле (2.4)
![]() ,
а модуль вектора
,
а модуль вектора
![]() ,
где
мгновенная угловая скорость конуса, а
,
где
мгновенная угловая скорость конуса, а
![]()
расстояние по перпендикуляру от точки
С
до мгновенной оси вращения конуса
,
(pис. 2.6).
На рисунке
расстояние по перпендикуляру от точки
С
до мгновенной оси вращения конуса
,
(pис. 2.6).
На рисунке
![]()
![]() .
.
Р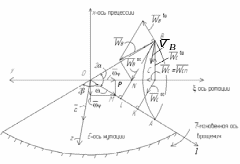 ис.
2.6
ис.
2.6
Тогда можно определить
![]() ,
,
![]() .
.
Стрелка на pис. 2.6
указывает, что вращение конуса 1
происходит по ходу часовой стрелки,
если смотреть с положительного конца
оси прецессии
![]() ,
поэтому
,
поэтому
![]() противоположна по направлению оси
.
противоположна по направлению оси
.
2. Далее по теореме синусов для векторного треугольника OMP (см. рис. 2.6) можно записать:
![]() . (2.7)
. (2.7)
Векторный треугольник
построен так, что
![]() (оси прецессии), а
(оси прецессии), а
![]() (оси ротации),
(оси ротации),
![]() (мгновенной оси вращения).
(мгновенной оси вращения).
Из (2.7)
![]() ,
,
![]() .
.
Определили угловые
скорости прецессии
![]() и ротации
и ротации
![]() ,
соответственно, причем
,
соответственно, причем
![]() .
.
Проанализируем результат:
 (2.8)
(2.8)
Имеем регулярную прецессию, так как выполняется условие (2.8).
3. При регулярной
прецессии вектор углового ускорения
конуса
определяется по формуле (2.3)
![]() .
.
Величину углового ускорения конуса определить по формуле
![]() ,
,
![]() (см. рис. 2.6).
(см. рис. 2.6).
Вектор углового
ускорения
![]() ;
в силу (2.2)
;
в силу (2.2)
![]()
4. Вектор скорости
точки В
определяется по формуле (2.3):
![]() .
.
Тогда величина
вектора скорости
![]() ,
где
,
где
![]()
кратчайшее расстояние от точки В
до мгновенной оси вращения
кратчайшее расстояние от точки В
до мгновенной оси вращения
![]() .
.
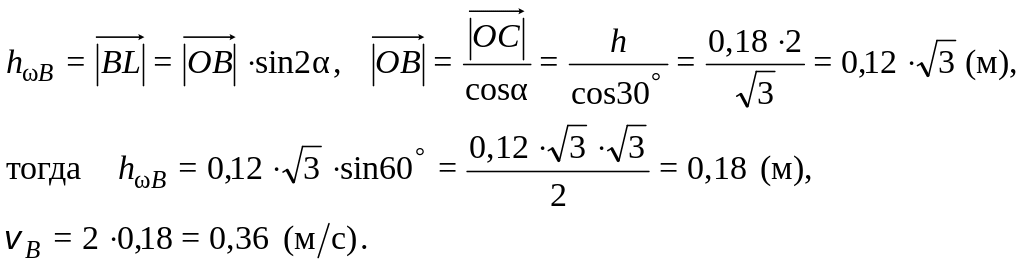
Вектор скорости
точки В
по направлению совпадает с осью
![]()
![]() (см. формулу (2.3)).
(см. формулу (2.3)).
5. Вектор ускорения
точки В
определить по формуле
![]() как векторную сумму осестремительного
и вращательного ускорений точки В.
как векторную сумму осестремительного
и вращательного ускорений точки В.
![]()
![]() (м/с2)
величина осестремительного ускоре-
ния
точки В.
(направление всегда известно по
наименованию
(см. рис. 2.6)).
(м/с2)
величина осестремительного ускоре-
ния
точки В.
(направление всегда известно по
наименованию
(см. рис. 2.6)).
Вектор вращательного
ускорения
![]() определить из
векторного произведения
(2.5)
определить из
векторного произведения
(2.5)
![]() ,
тогда
,
тогда
![]()
![]()
![]() (м/с2).
(м/с2).
Вектор
![]() и направлен в силу (2.5), как показано на
рис. 2.6.
и направлен в силу (2.5), как показано на
рис. 2.6.
Полное
ускорение точки В,
вектор
![]() определить по теореме косинусов (2.6):
определить по теореме косинусов (2.6):
![]() .
Угол
.
Угол
![]() =60°,
cos60°=0,5.
=60°,
cos60°=0,5.
Тогда
![]() (м/с2)
(с точностью до трех значащих цифр).
(м/с2)
(с точностью до трех значащих цифр).
Направление вектора
![]() (см. рис. 2.6) построить как диагональ
параллелограмма со сторонами
(см. рис. 2.6) построить как диагональ
параллелограмма со сторонами
![]() .
Обратить внимание на то, что угол между
не равен 90°, как это бывает при вращении
тела вокруг неподвижной оси.
.
Обратить внимание на то, что угол между
не равен 90°, как это бывает при вращении
тела вокруг неподвижной оси.
6. Точка
![]() ,
поэтому вектор ускорения
,
поэтому вектор ускорения
![]() можно определить как векторную сумму
касательного
можно определить как векторную сумму
касательного
![]() и нормального
и нормального
![]() ускорений точки С,
т.е.
ускорений точки С,
т.е.
![]() .
.
Касательное ускорение
![]()
![]() м/с2 = const,
м/с2 = const,
![]() ,
расстояние от точки С
до оси
,
расстояние от точки С
до оси
![]() ,
,
![]() .
.
Тогда вектор
ускорения точки С
совпадает с
ее нормальным ускорением
![]() ,
а величина
,
а величина
![]() = 0,18 (м/с2),
= 0,18 (м/с2),
![]() м/с2
ускорение точки С
(см. pис. 2.6).
м/с2
ускорение точки С
(см. pис. 2.6).
Вектор
![]() ,
направлен к центру О
окружности
радиуса
,
направлен к центру О
окружности
радиуса
![]() ,
по которой движется точка С
в результате прецессии.
,
по которой движется точка С
в результате прецессии.
Вращательное
ускорение точки С
определить
по формуле (2.5) векторного произведения
![]() .
.
Величина
![]() (м/с2),
(м/с2),
![]() =
=![]() м.
м.
Вектор
![]() и направлен, как на рис. 2.6,
см. форму-
лу (2.5).
и направлен, как на рис. 2.6,
см. форму-
лу (2.5).
З А Д А н и е К3
