Занятие 1. Декартовы координаты. Векторы и скаляры. Сложение и вычитание векторов. Действия над векторами, заданными своими проекциями. Скалярное произведение векторов. Направление вектора.

☺ ☻ ☺

Общие формулы:

Пусть = , = ; = , = .

Тогда: = = – = = = ,

= = – = = = .

Для вектора : , орт ; проекции вектора на оси координат: = , = , = , где – углы с осями координат ; = , = , = . Также: = .

Пусть имеем векторы: = и = . Для любых вещественных чисел и линейная комбинация векторов и записывается в виде:

= = = .

Скалярное произведение векторов и , угол между которыми равен , записывается в виде: = = , = . Также потребуются формулы: вычисление = = 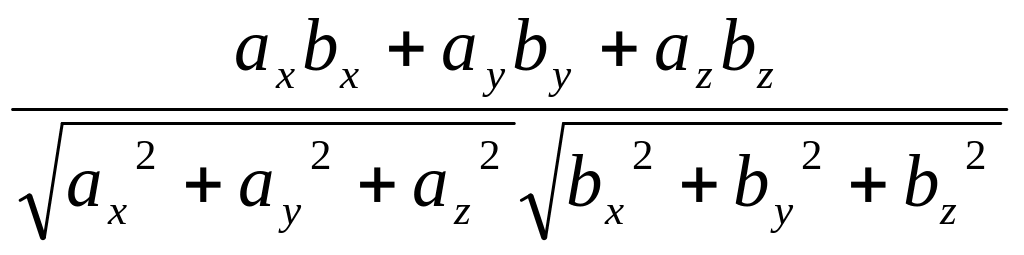и нахождение проекций: = и = .

••• ≡ •••

Пример 1–35: Заданы векторы: = (–1,2,0), = (3,1,1), = (2,0,1) и = –2 + . Вычислить: а) и координаты орта вектора ; б) ; в) координату вектора ; г) .

Решение:

Применяя общие формулы, решим каждую из поставленных задач:

а). Вычислим длину вектора : = = = . Вычислим единичный вектор для вектора : = = (–1,2,0).

б). Вычислим угла между вектором и осью : = = .

в). Используя линейные операции над векторами: сложение векторов и умножение вектора на число, вычислим координату вектора = =(–1) –2·3+ = .

г). Вычислим проекцию вектора на ось . Если бы мы имели и , то можно было бы воспользоваться формулой: = . Мы не имеем ни того ни другого, потому воспользуемся формулой из предыдущего пункта, но для проекции на ось : = = = =2 –2·1+ =0.

Ответ: по пунктам: а) = (–1,2,0), б) = , в) = , =0.

Пример 2–39: Заданы векторы: = , = , = . Вычислить: а) координаты орта ; б) координат вектора = ; в) разложение вектора = по базису ; г) вычислить .

Решение:

Замечание: предполагается, что все векторы заданы в трёхмерном пространстве с базисом .

Применяя общие формулы, решим каждую из поставленных задач:

а). Вычислим длину вектора : = = . Вычислим единичный вектор для вектора : = = (2,3,0).

б). Используя линейные операции над векторами: сложение векторов и умножение вектора на число, вычислим вектор =(2,3,0) +(1,1,–1) = .

в). Вычислим вектор . Задача не отличается от предыдущего пункта: =(2,3,0)+(0,–3,–2) – 2(1,1,–1)= (0,–2,0)= .

г). Воспользуемся формулой из предыдущего пункта, обозначив = . В таком случае имеем: = = =3 – =6.

Ответ: по пунктам: а) = (2,3,0), б) = , в) = , г) =6.

Пример 3–52: Даны две смежные вершины параллелограмма : (–2,6), (2,8) и точка пересечения диагоналей (2,2). Найти две другие вершины параллелограмма.

Решение:

Д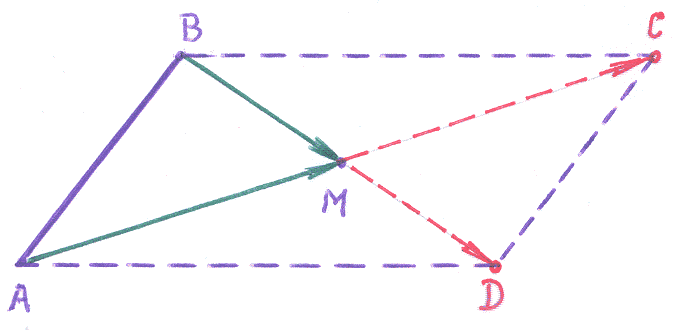 ля решения задачи удобно (хотя не обязательно!) воспользоваться эскизом параллелограмма: точное построение точек в системе координат не требуется!

1. Воспользуемся свойством диагоналей параллелограмма: точкой пересечения диагонали делятся пополам. Это значит, что можно записать равенства векторов: и .

2. Используя равенства векторов, запишем равенства для точек:

→ = =(6,–2);

→ = =(2,–4).

Ответ: вершины: =(6,–2); =(2,–4).

Пример 4–55: На оси ординат найти точку , равноудалённую от точек (1,–4,7), (5,6,–5).

Решение:

Замечание: для решения задачи удобно (желательно!) воспользоваться эскизом: точное построение точек в системе координат не требуется: для многих выполнение точного чертежа занимает много времени, кроме того затрудняет восприятие свойства универсальности формул!

Общие формулы: Пусть: = и = . Учтём правило построения направленного отрезка (геометрического вектора!): = . Тогда длина отрезка: = = .

1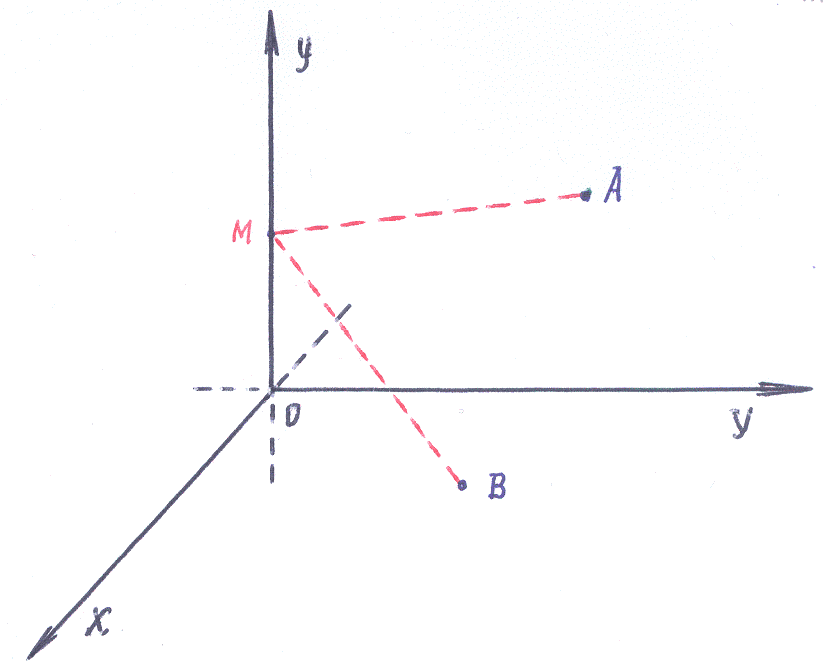 . Обозначим: = = и применим формулу для направленного отрезка:

=(1,–4,7) – = ,

=(5,6,–5) – = .

2. По условию точку нужно так расположить на оси , чтобы расстояния и были равными, то есть: = .

Мы воспользуемся равноценным ему равенством (так как длина есть величина положительная!): = . Применяя формулу для вычисления длины вектора, после несложных алгебраических преобразований, получим уравнение:

= , или: =1.

3. Получено единственное решение: = .

Замечание: в общем случае задача может иметь два решения (в том числе совпадающих!) или не иметь ни одного: это зависит от конкретного уравнения = .

Ответ: точка: = .

Пример 5–66: Заданы модули векторов: =3, =5. Определить, при каком значении векторы = и = будут перпендикулярны.

Решение:

З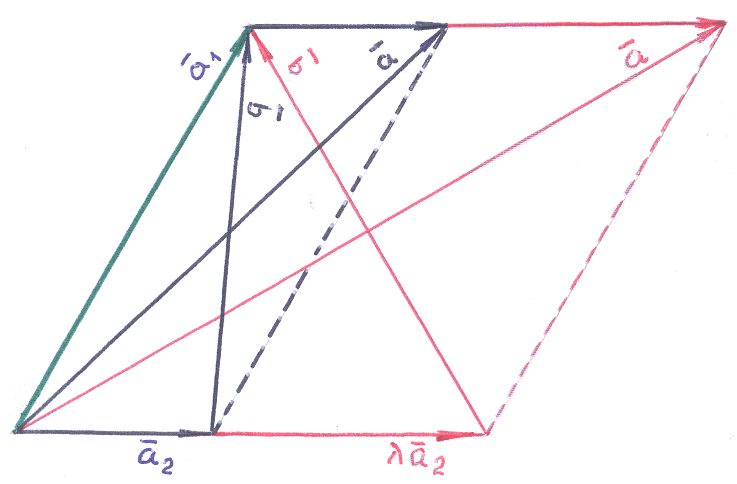 амечание: для решения задачи удобно (желательно!) воспользоваться эскизом: точное построение точек в системе координат не требуется: здесь важно прочувствовать, как параллелограмм превращается в ромб за счёт выбора параметра !

Общие формулы: учитывая правило графического представления суммы и разности векторов, видим, что векторы и есть диагонали параллелограмма; из геометрии следует, что за счёт выбора значения должен получиться ромб, то есть = ; мы воспользуемся признаком перпендикулярности векторов: =0.

Из свойства скалярного произведения следует равенство: = = = =0. Это значит: = . Графическое изображение ромба в случае = не вызывает затруднения!

Ответ: значение: = .

Пример 6–78: Заданы векторы: =(4,–2,–4), =(6,–3,2). Вычислить: а) скалярное произведение векторов ; б) ; в) ; г) .

Решение:

Применяя общие формулы, решим каждую из поставленных задач:

а). Вычислим = =22.

б). Вычислим . Можно было бы вычислить векторы = и = , затем воспользоваться формулой . Мы воспользуемся результатом а): сначала вычислив: = – использовано распределительное свойство. Вычислим: =36, =49 → = =200.

в). Вычислим = и воспользуемся результатами пунктов а) и б): = =41.

г). Вычислим вектор = =2(4,–2,–4)–(6,–3,2)=(2,–1,–10) → = .

Замечание: можно все вычисления выполнить в координатной форме: определяет автор решения задачи!

Ответ: по пунктам: а) 22, б) 200, в) 41, г) .

Пример 7–82: Доказать, что четырёхугольник с вершинами: (–3,5,6) , =(1,–5,7) , =(8,–3,–1) , =(4,7,–2) есть квадрат.

Решение:

Алгоритм: 1) убедимся, что = , это значит, что – параллелограмм;

2) проверим равенство сторон = , это значит, что – ромб;

3) убедимся, что · =0, это значит, что – ромб.

Р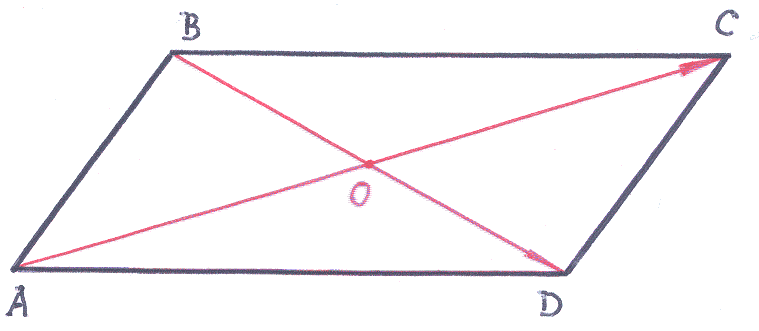 еализуем принятый алгоритм:

1). Вычислим векторы и :

= =(1,–5,7)–(–3,5,6)=(4,–10,1), = =(8,–3,–1)–(4,7,–2)=(4,–10,1),

подтверждено: = .

2). Вычислим вектор :

= =(4,7,–2)–(–3,5,6)=(7,2,–8). Вычислим: = и = , подтверждено: = .

3). Вычислим векторы · =(4,–10,1)·(7,2,–8)= =0: – ромб.

Замечание: возможны и другие варианты решения задачи!

Ответ: показан алгоритм доказательства и его реализация: доказано.

Пример 8–84: Вычислить работу силы = при перемещении материальной точки из положения (–1,2,0) в положение =(2,1,3).

Решение:

Замечание: в условии задачи следует добавить: перемещение из положения в положение происходит по прямой линии!

1). Вычислим перемещение = = =(2,1,3)– (–1,2,0)=(3,–1,3).

2). Вычислим работу силы: =| |·| | = · =(1,2,1)·(3,–1,3)= =4.

Ответ: работа: =4.