1

Теория вероятностей

Случайные события. Пространство элементарных событий. Алгебра событий.

Событие – любой исход эксперимента (всякий факт, который в результате опыта может произойти или не произойти).

Случайные – не можем предвидеть (подбрасывание монеты).

А – появление герба при бросании монеты;

В – попадание в цель при выстреле;

С – появление туза при вынимании карты из колоды.

Пространство элементарных событий.

I эксперемент эл.исходы: W₁ – вып. «1»

W₂ – вып. «2»

W₆ – вып. «6»

Сложн.событ. (выпис.четное): А=

Выпадение очков кратное 3: В=

Пространство эл-ных событий – множество всех элемент.исходов данного эксперемента.

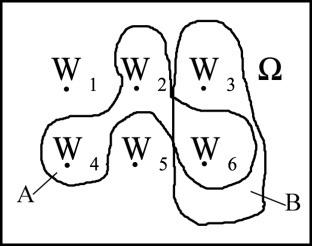
II эксперимент – подбрас.2 игр.кости

(1,1) (1,2) … (1,6) Ω

(2,1) (2,2) … (2,6)

. . . . . . . .

(6,1) (6,2) … (6,6)

Сложное соб.А – подмн-во Ω

Алгебра событий – совокупность событий, на кот.опр-ны операции:

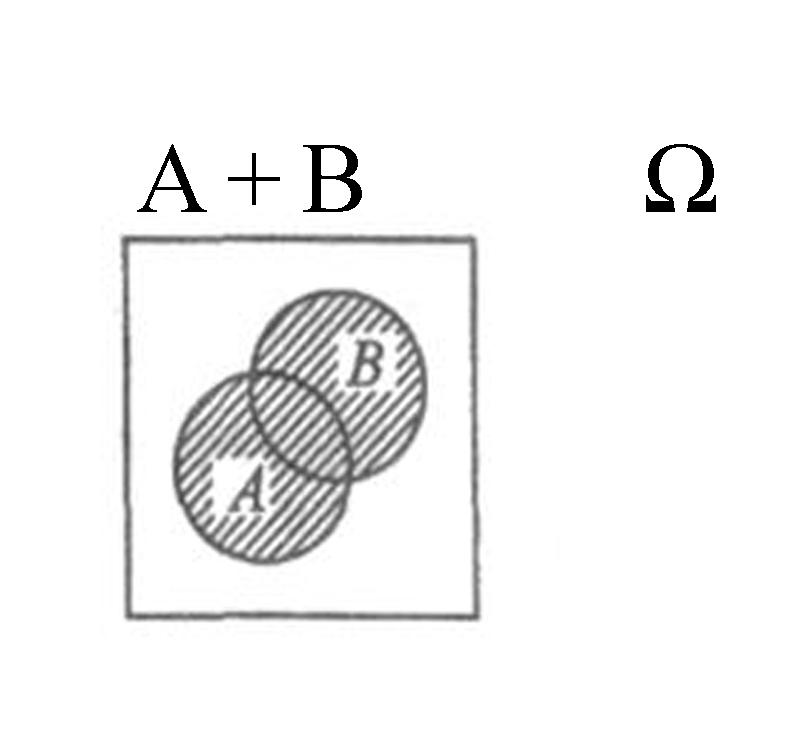
А+В – событие, состоящее в том, что либо происходит А, либо В, либо А и В.

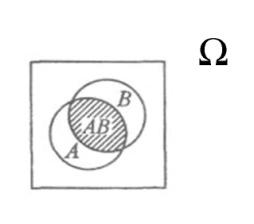
АВ – событие, состоящее в том, что А и В происходят вместе.

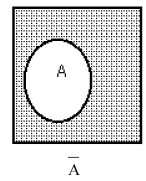
Ā – (отрицание) – событие, состоящее в том, что А не происходит.

Пример:

А+В=

AB=

Ā=

Ω - достовер.соб., кот.происходит всегда

Ø = ᾯ (напр. Выпадение «7» на кубике)

2

Вероятность соб. –численная мера степени объективной возможности этого события. (связано с понятием частоты соб-я)

Более вероятные – кот. происходят чаще;

Мало вероятные – кот. почти никогда не происходят.

Два события А и В назыв. несовместимыми если они не могут одновременно произойти.

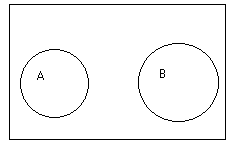
Вероятность – некот.число, кот.лежит от 0 до 1, показывает насколько часто происходит событие в серии экспериментов.

Вероятность в дискретных и непрерывных пространствах элем.событий.

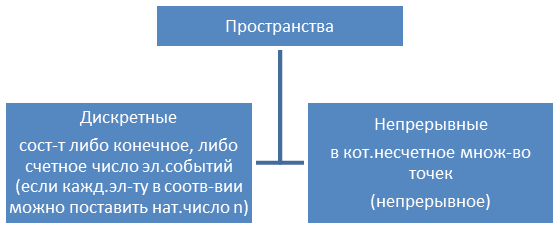
Пр.: монета подбрасываемая до появления герба

Ω=

Р(А) – вероятность соб.А

(числ.мера степени объективной возможности того события – частота)

Аксиоматически:

экспер→дискр.пр.эл.соб.→

Свойства:

P(

Свойства вероятности:

Р(Ø)

Р(Ω)=1

n

P(A+B) = P(A) + P(B) – P(AB)

AB=Ø P(A+B) = P(A) + P(B)

P(Ā) = 1 – P(A)

Классическая схема равновероятных событий

Равновероятные события

Если W_i новероятны или равновозможные (ни одно из этих событий не явл.объективно более возможным, чем другое)

=N – число эл.иск. в Ω

i=1,2,…N

P(A)== ← Формула классической вероятности

Р(А)=

0

Благопр.случай – появление этого случая влечет за собой появление данного соб.

Комбинаторика

Выборки: Упорядоченные:

С возвращением (с повторением)

Без возвращения

Неупорядоченные

С возвращением (с повторением)

Без возвращения

3

Теоремы сложения и умножения вероятности.

Р(А+В) = Р(А) + Р(В) – вероятность суммы 2-ух несовместных событий равна сумме вероятностей этих событий.

;

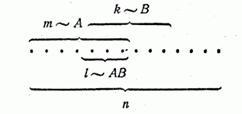
Нет случаев, кот.благопр. и А, и В вместе →

P(A+B+C) = P(A) + P(B) + P(C)

)

Следствие 1. Если соб. образуют полную группу несовместимых событий, то сумма их вер-тей равна 1.

Следствие 2. Сумма вероятностей противоположных событий равна 1;

Р(А) + Р(Ā) = 1

Р(А+В) = Р(А)+Р(В)-Р(АВ) – для совместимых

Р(А+В+С)= Р(А)+Р(В)+Р(С)–Р(АВ)–Р(АС)–Р(ВС)+Р(АВС)

Р(АВ)=Р(А)+Р(В)+Р(С)-Р(А+В)-Р(А+С)-р(В+С)+Р(А+В+С)

2)Соб.А назыв. независимым от соб.В, если вер-сть соб.А не зависит от того, произошло соб.В или нет.

Подбррас.2 монеты:

А – появление герба на 1ой монете.

В – появление герба на 2ой монете.

Условная вероятность – вер-сть соб.А при условии, что соб.В произошло. Р(А∕В)

Р(А∕В)=Р(А) – условия независимости.

Теорема умножения

Р(АВ)=Р(А)Р(В∕А) вероятность произведения 2ух событий равна произведению вер-сти одного из них на условную вер-сть другого, вычисл.при условии, что первое имело место. (для зависимых соб.)

Р(АВС)=Р(А) Р(В∕А)Р(С∕АВ)

Док-во:

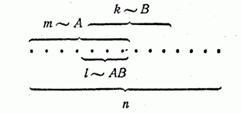
Р(АВ)=Р(А)*Р(В) необх. и дост.усл.независ-ти.

Следствие 1. Если, соб.А не зависит от соб.В, то и соб.В не зависит от соб.А.

Следствие 2. Вероятность произведения 2ух независимых событий равна произведению вер-тей этих событий.

4

Формула полной вероятности и формула Байеса.

Формула полной вер-сти явл.следствием обеих основных теорем.

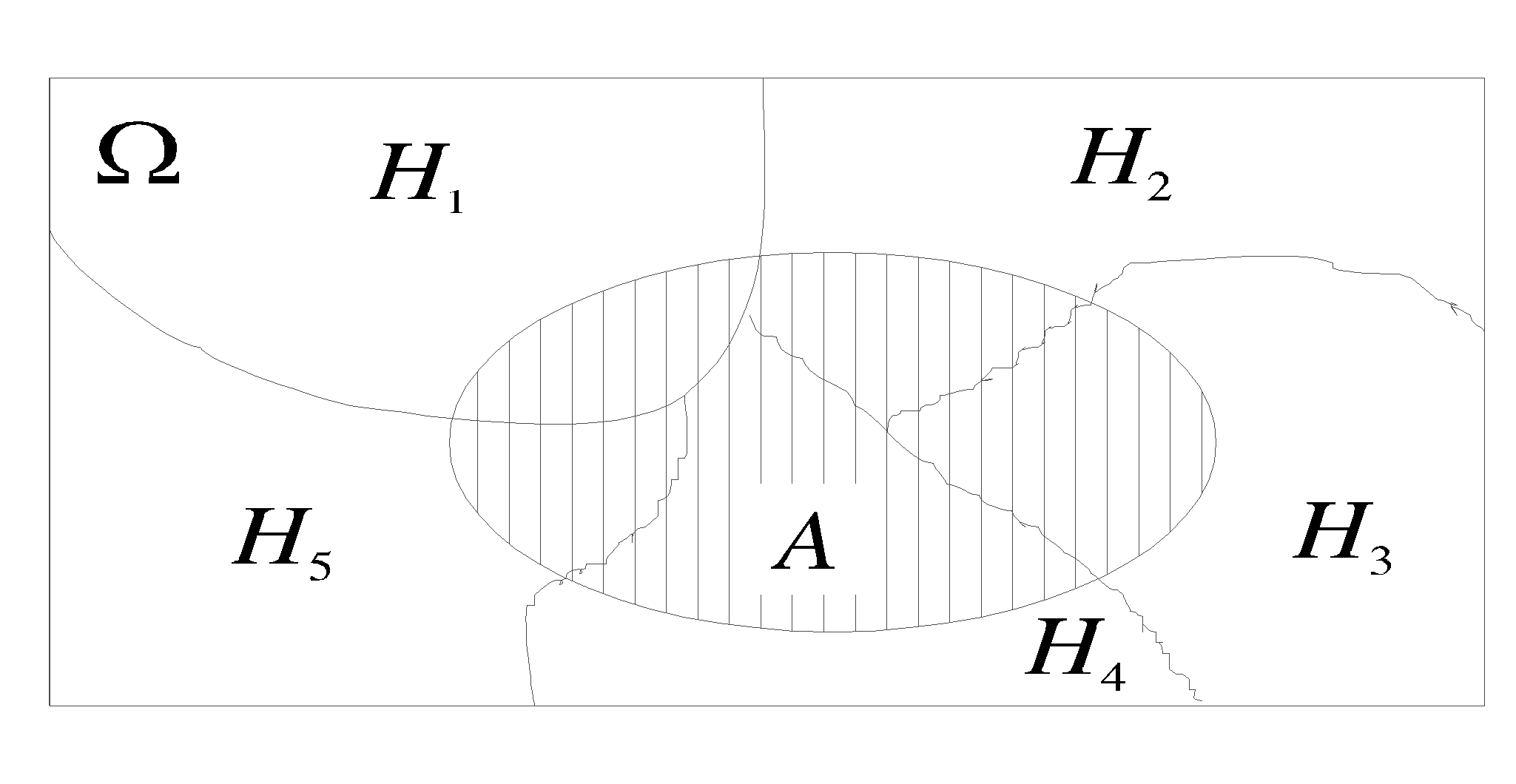
(гипотезы)

Н_1, Н_{2, …}Н_{к –} полная группа событий или разбиение Ω, если:

Н₁+ Н_2,+ _…+Н_к=Ω

Не пересекаются между собой

H_i*H_j=Ø i≠j I,j=1,2,…k

A=AH₁+AH₂+AH₃+…+AH_k (все слагаемые АН_i несовместны)

Р(А)=Р(АН₁+АН₂+…+АН_к)=Р(АН₁)+Р(АН₂)+…+Р(РН_к)=Р(Н₁)Р(А∕Н₂)+…+Р(Н_к)Р(А∕Н_к)

– формула полной вероятности.

Формула Бейеса (теорема гипотез) явл.следствием теоремы умножения и формулы полной вер-сти. (необх-мо найти усл.вер-сть Р(Н_i∕A) для каждой гипотезы.

Пр. Из какой урны более вероятно вытащить бел.шар? (Н₁ или Н₂)?

Р(Н₁∕A) V Р(Н₂∕A)

Р(Н_i∕A)= вычисл.по формуле полн.вер-сти

5

Дискретные сл.в. Ряд распределения. Числовые характеристики.

Ω=

Случайная величина

X=X(W_i)числ.ф-ция, определенная на каждом элементарном исходе. (пространстве элем.соб.)

X₁=X(W₁)

X₂=X(W₂)

Случайная величина – величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Пр.

1. число попаданий при 3х выстрелах (0;1;2;3)

2. число вызовов, поступивших на телефон.станцию за сутки (1;2;3;4….)

3. частота попаданий при 10 выстрелах (0;0,1;0,2;….10)

дискретные – можно заранее перечислить

непрерывные – непрерывно заполняют некоторый промежуток.

Пр.

1. абсцисса точки попадания при выстреле;

2. ошибка взвешивания тела на аналитич.весах;

3. скорость летат.аппарата в момент выходп на заданную высоту;

4. все наугад взятого зерна пшеницы.

(границы неопределенные, расплывчатые)

Производится опыт соб.А – может появиться, а может и нет.

Вместо соб.А расмотр.сл.вел.Х, кот.=1

Если соб.А не происходит Х=0

Х – характеристическая сл.вел.соб.А

Х – сл.вел.

Х₁,Х₂….Х_n – возможные значения сл.вел.Х

Ряд распределения

Закон распределения – всякое соотношение, устанавливающее связь между возможными значениями сл.вел-ны и соответствующими им вероятностями.

Простейшей формой задания закона распределения дисер.сл.вел.Х явл. таблица, в кто.перечислены возможные значения сл.вел. и соответствующие им вероятности.

1) ряд распределения сл.вел.Х

2)

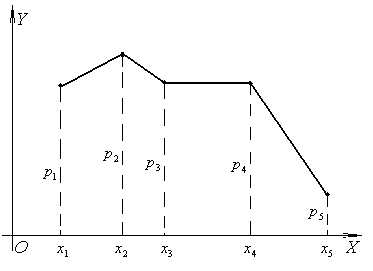многоугольник распределения (один из форм закона распределения)

3)иногда удобной оказывается «механическая» интерпретация ряда распред-я (система матер.точек с какими-то массами, расп.на оси абсцисс)

Числовые характеристики дискр.сл.величины

Числ.хар-ки – хар-ки, кот.характер-ют различн.св-ва случ-ной вел.

Характеристики положения

(мат.ожид-е, мода, медиана)

Указывают некоторые среднее ориентировочное значение, около которого группируются все возможные значения случ.вел.

1. Мат.ожидание - сумма произведений всех возможных значений сл.вел. на вероятности этих значений.

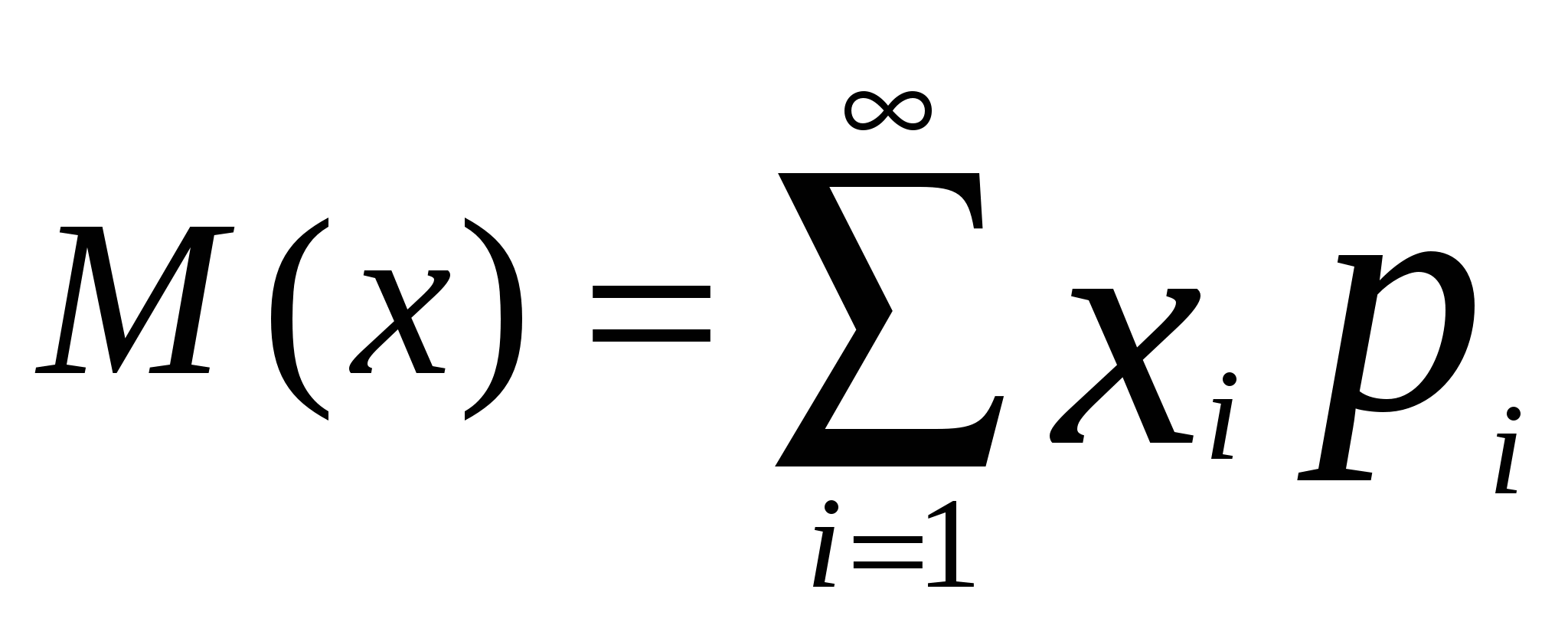
при большом числе опытов среднее арифмет.наблюденных значений сл.вел.приближается (сходится по вероятности) к ее матем.ожиданию.

М(Х) – абсцисса центра тяжести системы матер.точек.

Свойства М(х):

1)М(Х+а)=М(х)+а, а =const

2)М(аХ)=аМ(х)

3)М(Х+Y)=M(X)+M(Y)

4)h(X) – ф-ция Х, тогда

5) M(a)=a

2)Мода – наиболее вероятное значение (М)

3)Медиана : Р(Х

Моменты. Дисперсия. Среднее квадратическое отклонение.

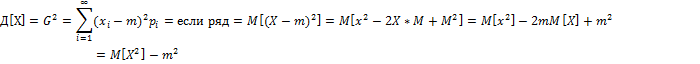
- определяет разброс отн-но (хар-ка рассеивания)

Дисперсия – мат.ожидание квадрата соответствующей центрированной величины.

Среднее квадратич.отклонение G=

(для наглядной характеристики рассеивания)

Размерность совпадает с размеренностью сл.вел.

Свойства :

1. Неотрицательная 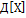=0

2. С-константа,

3. 

4. 

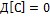
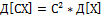
Моменты (опис.св-ва распр-я):

Начальные

d_k

k=0,1,2….

d=1

=m

= хар-ка формы распределения

Центральные

М_к

M₀ = 1

M₁ = M=0

M₂ = M=Д

M₃ - хар-ка формы распред-я

Хар-ка формы распределения:

Асимметрия

A_s(X)

A_s(X)=

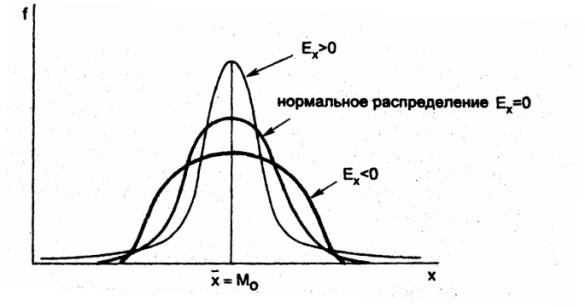
Эксцесс

Е_х(Х)

Центрированная сл.вел. – отклонение сл.вел.Х от ее мат.ожид-я Х=Х-М_х

6

Повторение испытаний. Схема Бернулли. Биномиальное распределение. Формула Пуассона.

Один и тот же опыт повторяется соб.А может появиться или нет.

Нас интересует не результат каждого отдельного опыта, а общее число появлений соб.А в резте серии опытов.

Пр.число попаданий среди группы выстрелов.

Х~В(n₁,p) – случ.вел.Х имеет биноминал.распр-е с параметрами n и p.

Схема Бернулли: (идеализир.ситуация) (если n=1)

Исходы эксперемента: «успех» (А)

«неуспех» (Ā)

К- число успехов в n исп-нии.

Р(А)=р

Р(Ā)=1-р=q

Эксперимент повторяется n раз, р и q не изменяются.

Рассм.случ.вел.Х – число успехов в n испытаний по схеме Бернулли.

Х=0,1,2,…n (целочисл.дискр.знач-я)

M(X)=n*p

Д(Х)=n*p*q

P(AA….A ĀĀ….Ā)= (для конкр.посл-сти)

Если n большое, то в силу ЦПТ В(n,p)N(np;npq)

Если n большое, а - фикс.число, то

Приближенная формула Пуассона

n – велико

p – мало

0,1 n*p10

где =n*p

Док-во формулы

7

Распределение Пуассона. Геометрическое распределение.

Распределение Пуассона (Закон редких событий)

Дискр.сл.вел.Х=0,1,2,… имеет распр-е Пуассона с параметром , если вероят-сть того, что она примет определение значения к, выражается формулой.

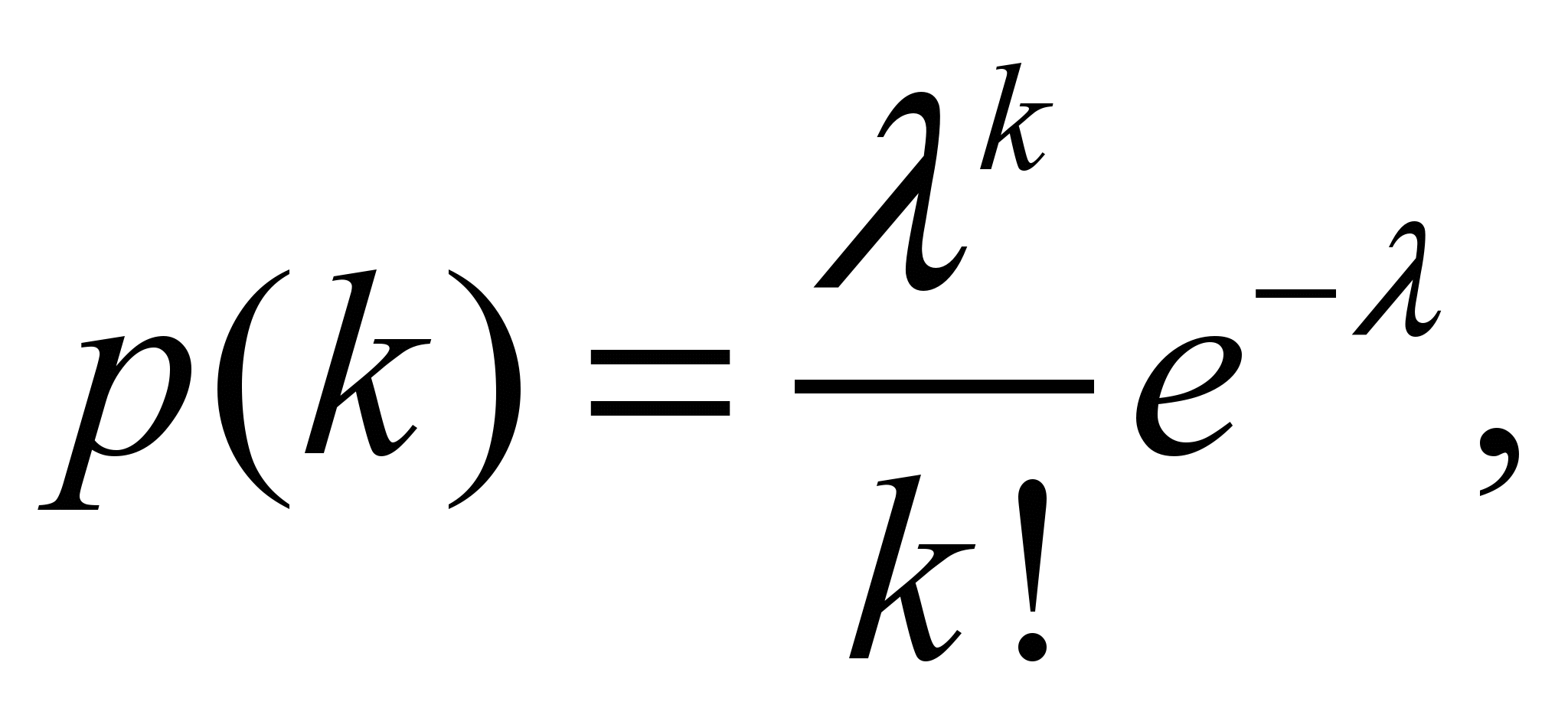
К=0,1,2,…

=n*p

Редкое событие: стоим на перекрестке и подсчит.число столкновений.

Физич.модель, приводящ.к распределению Пуассона.

Поток событий – посл-сть некот.случ.соб-тий во времени.

Постулаты:

1. Поток явл.стационарным

2. Отсутствует последствие (т.е.без памяти)

3. Поток явл.ординарным

Вероятность того, что на интервале t произойдет к событий =

Поток явл.стационарным, если данная вер-сть произойдет независимо от времени.

Ординарность: можно найти столь малый интервал , для которого вер-сть того, что на произойдет 1 соб-е произойдет 2 и более событий при

Распр-е Пуассона играет ключ.роль в теории массового обслуживания.

Пр.

1. Поток входящих телефон.звонков;

2. Поломки оборудования;

3. Длит-сть исполнения ремонтных работ стабильно работающим сотрудником;

4. Ошибка печати;

5. Дефекты в длинной ленте или цепи.

Геометрическое распределение

p- вер-сть успеха

q- вер-сть неуспеха

p и q неизмен. Испытания независима дгур от друга.

Х – число эксперементов, кот. необх-мо произвести до появ-я 1-го успеха.

Х=1,2…..

K=1,2,3….

M

8

Непрерывные сл.вел. Функция распределения и плотность распределения и их свойства. Равномерное и экспоненц.распр-я.

Непрер.случ.вел. – числ.ф-ция, кот.задана на пространстве эл.событий.

Пример: время работы, время работы прибора.

Плотность распределения.

Берем еденич.массу и распределяем по мн-ву случ.вел.

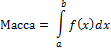
F(x) – плотность распр-ния массы (вероятностей)

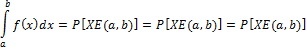
Свойства f(x):

1)ф-ция неотриц. f(x)0

2)

3)

Функция распределения.

Свойства f(x):

1. 

2. 

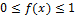
3. Механич. интерпретация f(x)

4. 

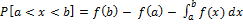
Равномерное распределение.

- интервал. (вероятность любого интервала зависит только от его длины)

F(x)=

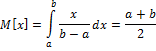
Д(X)=M(

Применяется: ошибка округления.

Экспоненциальное распределение.

(моделирующее время между 2-мя последовательными свершениями одного и того же события)

Пр.

1)время отказа аппаратуры;

2)время между 2ух последовательных покупателей;

3)время ожидания автобуса на остановке

(отсутствие памяти – кол-во времени, затрач.на ожидание автобуса, не влияет на время, кот.ему придется прождать)

Д(Х)=

Ех( - частный случай распр-ния хи-квадрат

9

Свойства мат.ожидания и дисперсии. Квантили. Мода, медиана, асимметрия и эксцесс.

1. 

2. 

3. 

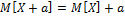
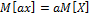
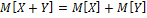
4. h(x) – ф-ция Х

5. 

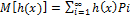
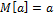
1. Неотриц. Д(х)

2. Д

3. Д

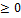
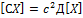
4. Д

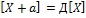
Квантиль

Пусть сл.вел.Х имеет f(x), F(x)

Квантилью порядка р(0р1) Хр назыв.абсцисса, кот.определяет от себя слева на графике плотности площадь = р.

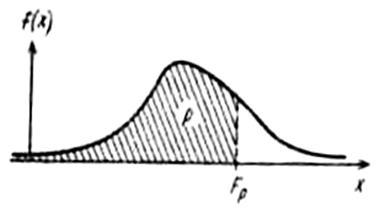
Способы определения квантили

1. 

2. 

h_x - квантиль порядка 0,5 (медиана)

Мода – значение, в котором плотность вероятности max.

Полимодальное распр.- более 1 max.

Антимодальное - посредине min.

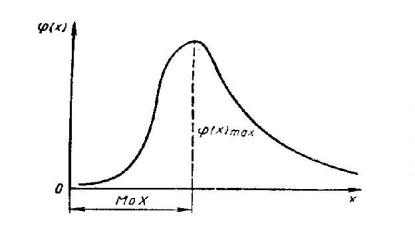
Медиана – значение, для которого одинаково вероятно, окажется ли сл.вел.меньше или больше h_x.

Геом.медиана – абсцисса точки, в кот.площадь, огранич.кривой распределения делится пополам.

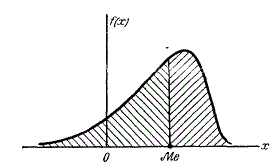
Хар-ка формы распределения.

Асимметрия

Хар-ка «скошенности» распределения

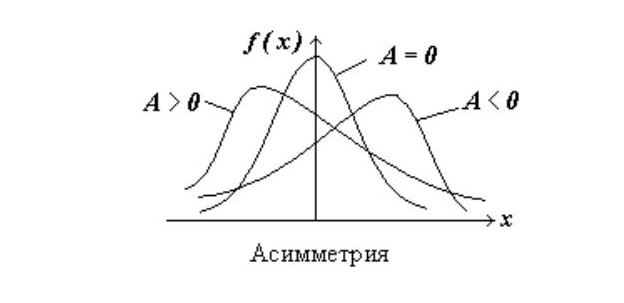
Экцесс

Хар-ет форму распр-я в окр-сти вершин (хар-ка «крутости»)

Если m,r)

10

Нормальное распределение (Гаусса)

Вероятность попадания в интервал симметричный относительно М(х).

Ассиметрия и эксцесс распределения. Стандартизированное норм.распр-е и его свойство. Правило 3 сигм.

Явл.предельным законом, к котор.приближаются другие законы распр-я при весьма часто встречающихся типичных условиях.

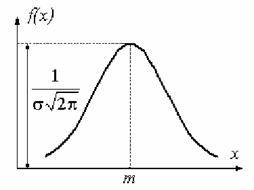
Замена:

- центр рассеивания.(особенно в задачах стрельбы).

Вероятность попадания в интервал.

Замена:

X=

dx=

=

Свойства:

1)

2)

3)

4)

;

m=h=d

Стандартизованное нормальное распределение.

Стандартизация:

1 этап (центрированный): X-m

– стандартиз.сл.вел.

x) – плотность распр-я.

x)=

Функция распр-я: x)=

Правило 3 сигм:

P

11

Системы дискретных сл.вел.

Таблица распределения. Независимость. Ковариация. Условные распределения. Системы непрерыв.сл.вел.

Рез-т опыта описывается не 1 сл.вел., а 2умя или >сл.вел-нами, образующими комплекс или систему.

(напр.: точка попадания снаряда опр-тся абсциссой и ординатой)

При рассмотрении вопросов, связан.с сист.сл.вел.удобно пользоваться геом.интепретацией системы.

(напр.(X,Y) можно изобразить случайной точкой на плоскости с коорд-ми X и Y.

Часто вместо образа случ.точки пользуются образом случайного вектора.

(X,Y) – случ.вектор с коорд-ми

Х=Х_1,Х₂, …Х_к

Y=Y₁,Y₂,…Y_k - дискр.сл.вел.

- закон распр-я для (X,Y)

Ф-ция распр-я.

Y X	X1	X2	…	XK	Σ
Y1	P11	P21	…	PK1	PY1
Y2	P12	P22	…	PK2	PY2
…	…	…	…	…	…
yn	P1n	P2n	…	Pkn	Pyn
Σ	Px1	Px2	…	Pxk

Крайние маргинальные распределения.

Р_у1*Р_х1=Р₁₁

X и Y независимы.

(если хотя бы 1 невыполн., то зависимы)

Условные распределения.

Независимость случ.вел-н.

(не завис.от того, какое значение приняла др.величина)

X и Y независ.сл.вел., если:

, т.е.усл.вер-сть совпадает с безусловной.

Если X и Y независимы, то необх.и дост.усл-е независ-сти величин.

Ковариация.

Мат.ожидание произведения центрированных случ.величин.

Cov(X,Y)=M

Cov(X,Y)=

Свойство: если X и Y независимы, то

(однако обратное неверно, т.е. если , то не обязат.независ.)

- ковариац.мтр

=

Системы непр.сл.вел.

Распр.системы непр.вел.обычно хар-ют не ф-цией распр-, а плотностью распр-я.

F(X,Y) – плотность распр-я

1. F(X,Y)

2. 

12

Мат.ожидание и дисперсия суммы сл.в. Мат.ожидание произв-я сл.в.

Если зависимы

Если независ.

13

Коэф-т корреляции как хар-ка статистич.связи. Некоррелир-сть и независимость сл.вел.

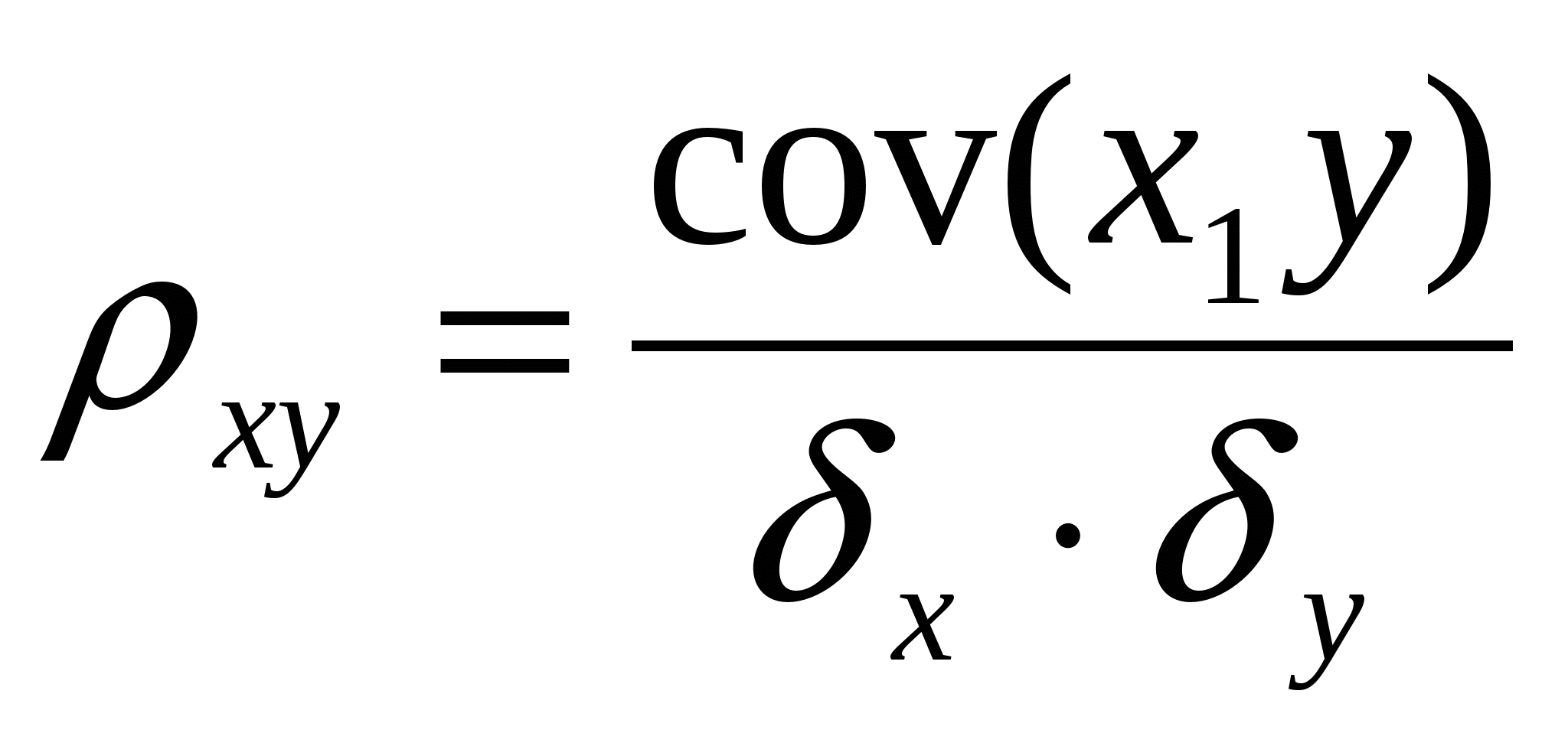
Если X и Y независимы, то

Свойства:

1.

2. если , то между X и Y имеется лин.зависимость Х=a+b*Y

3. Показыв.степень лин.завис-ти, когда Чем ближе к 1, тем коэфф.корреляции. (мера (индикатор) лин.зав-сти между X и Y)

14

Законы больших чисел и предельные теоремы. Теорема Бернулли. Теорема Чебышева.

При очень большом числе сл.явлений средний их рез-т практически перестает быть случайным и может предсказан с большой степенью определенности.

1. Сходимость по вер-сти

Х₁,Х₂,…Х_n

Посл-сть сходится по вер-сти к сл.в.А при

при большом числе опытов частота соб.приближается в вер-сти этого соб.

Если сущ. то и , что

2. Неравенство Чебышева

Пусть Х – любая сл.вел.

t0 – люб.число

=1

Каково бы ни было положит.число , вер-сть того, что вел.Х отклонится от своего мат.ожидания не меньше, чем на огранич.сверху.

Предельные теоремы дают возможность не только осущ-ть научн.прогнозы, в обл-сти сл.явл-ний, но и оценивать точность этих прогнозов.

(Закон больших чисел)

Предельные теоремы дают возможность не только осущ-ть научн.прогнозы, в обл-сти сл.явл-ний, но и оценивать точность этих прогнозов.

(Закон больших чисел)

Теорема Чебышева.

Пуст ь Х₁, Х₂, …Х_n – незав.сл.вел. имеют одно и тоже расрп-е.

Тогда

При достаточно большом числе независ.опытов со.ариф-ое наблюденных значений сл.вел.сходятся по вер-сти к ее мат.ожид-ю.

Док-ство: воспольз.нер-вом Чебышева.

Сл.в.Х

, t=const

Сколь угодна сход.по вер-сти близка к 1

Теорема Бернулли. (следствие т.Чебышева)

(устанавл.связь между астотой соб.и его вер-стью).

Пусть проводится (n) экспериментов. В каждом эксперименте появл.соб.А (успех) с вер-стью (р).

И появл.(Ā) (неуспех) с вер-тью q=1-p

Рез-ты экспер-тов не влияют друг на друга.

При неогранич.увеличении числа опытов h частота соб.А сходится по вер-сти к его вер-сти р.

k – число успехов в n испытаний; n –число экспер-тов.

15

Центральная предельная теорема. Теорема Муавра-Лапласа.

(колич-ная форма закона больших чисел)

Все формы ЦПТ посвящены установлению условий, при кот.возникает норм.закон распр.

N(m,

В теории стрельбы N(m, играет особо важную роль, т.к в боль-ве случаев практики корд-ты точек попадания и точек разрыва снарядов распределяются по норм. Закону.

Х₁, Х₂, …Х_n – незав.сл.вел.с одним и тем же распр-ем

X= Х₁+ …+Х_n – сумма случ.вел.

Рассм.нормир-ную случ.вел. (

Ф-ция растр-я равномерно по х.

Ф-ция распр-я норм.зак.с пар-ми N(0;1)

Следствие ( ЦПТ)

1. Х=

)

2. 

3. 

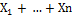
4. Теорема Муавра-Лапласа.

Х=

Напр.число успехов лежит в интервале (a,b)

16

Распределение сред.ариф-го независ. с.в. и отн-ной частоты при большом числе наблюдений n.

Среднее ариф.сл.вел.

Х₁, Х₂, …Х_n – незав.сл.вел., имеющ.одно и тоже распр-е

Среднее арифм.(выборочное среднее)

Относит.частота и свойства.

n – объем выборки

к – число эл-тов выборки, кот.облад.св-вом А относит.частота появления св-ва А

	0	1
	q	p

Статистика.

17

Предмет мат.статистики. Осн.понятия: выборка, генер.сов-сть статистики. Распр-е выборки, выборочные моменты. Выборочный вектор.

Мат.статистика позволяет получать обоснован.выводы о параметрах, видах распр-й и др.св-вах сл.вел.по конечной совокупности наблюдений над ними – выборке. (предмет: описание и анализ данных наблюдений).

Выборка – мн-во случаев, с помощью определен.процедуры выбран.из ген.сов-сти для участия в исследовании.

Ген.сов-сть – сов-сть всех объектов (единиц), отн-но которых ученый намерен делать выводы при изучении конкр.проблемы.

Мн-во всех обследуемых объектов.

Статистика – измеримая числовая ф-ция от выборки, не зависящих от неизвестных пар-ров распр-я.

-осн.хар-ки ген.сов-сти (среднее дисперсия, т.д.)

Выборка должна быть репрезентативной. (давать правильное представл-е о ген.сов-сти)

Простой случ.выбор – все эл-ты ген.сов-сти должны иметь равные шансы попасть в выборку.

Закон распр-я сл.вел.Х назыв. распределением ген.сов-сти, а случ.вектор (Х₁,Х₂,…Х_n) – выборочным вектором.

Часто требуется охарак-ть ген.сов-сть некоторыми колич.показателями, кот.определяют положение центра распр-я, рассеяние (разброс) и асимметрию, что дает возможность сравнить одну сов-сть данных с другой.

По выборке можно определить приближенные значения (оценки) этих числ.хар-к, кот.называются выборочными характеристиками.

Оценки моментов:

+

Распр-е выборки – распр-е дискр.сл.вел., приним.значения Х₁,Х₂,….Х_n с вероятностями 1∕n.

18

Задача стат.оценивания. Несмещенность и состоятельность оценок, эффективность оценок.

Задача – нахождение приближенных значений – оценок параметров распределения по выборке.

Статистика – некоторая ф-ция эл-тов выборки.

Вид распр-я известен

Критерии для выбора наилучшей оценки.