
- •2).Неопределенности вида (∞/∞),(0*∞),(∞-∞).Вторая теорема
- •1) (Критерий монотонности функции, имеющей производную на интервале).
- •2) (Достаточное условие строгой монотонности функции, имеющей
- •3) (Критерий строгой монотонности функции, имеющей производную на
- •1. ∢ Точку X∈( - , )
- •X0 принадлежащий (a; b) и проведем через точку m0 касательную.
- •1.Вычисление s плоской фигуры
- •2.Задача о вычисление пути прямолинейного движения
- •30. Понятие спрямляемой кривой. Вычисление длины гладкой прямой.
- •33. Общая схема применения определенного интеграла в физике. Примеры.
- •35.Поняти несобственного интеграла 2-го рода. Свойства. Признаки сходимости.
- •25. Понятие квадрируемости и площади плоской фигуры. Критерий квадрируемости. Свойства квадрируемых фигур.
- •26. Квадрируемость и вычисление площади криволинейной трапеции. Следствия из основной формулы.
- •27. Понятие кубируемости и объема тел. Первый критерий кубируемости. Объем прямого кругового цилиндра.
25. Понятие квадрируемости и площади плоской фигуры. Критерий квадрируемости. Свойства квадрируемых фигур.
Каждый многоугольник M имеет площадь S(M) .
Многоугольник – это объединение конечного множества треугольников.
Треугольник – это множество точек в плоскости ограниченой трехзвенной ломаной ABCA
Свойства
S(ед.кв)=1
М1 М2 => S(M1) ≤ S(M2)
M = M1 U M2 :
 ∩
∩
 = Ø } => S(M) = S(M1)
+ S(M2)
= Ø } => S(M) = S(M1)
+ S(M2)S(M) є [0;+∞)
Плоскасть Ф считается ограниченной
М (Ф) – Входящий в Ф – (В)
(Ф) М – Объемлющей (О)
(В) (Ф) (О) => S(В) ≤ S(О)
{S(B): (В) (Ф)} ограничено сверху => существует sup{S(B): (B) (Ф)} = S(Ф) нижняя площадь (Ф)
 (Ф)
= inf{S(O):
Ф
(О)} – верхняя площадь фигуры (Ф)
(Ф)
= inf{S(O):
Ф
(О)} – верхняя площадь фигуры (Ф)
S(B)
≤
 (Ф)
≤
(Ф)
≤
 (Ф)
≤ S(O)
(Ф)
≤ S(O)
Определен: Фигура называется квадрируемой, если её верхняя и нижняя площади совпадают при этом их общее значение называется площадью этой фигуры.
Критерий квадрируемости – плоская фигура (Ф) квадрируема тогда и только тогда, когда существует последовательность входящих многоугольников (В) и полследовательность (О) таких, что S(B)→S; S(О)→S
26. Квадрируемость и вычисление площади криволинейной трапеции. Следствия из основной формулы.
Критерий квадрируемости – плоская фигура (Ф) квадрируема тогда и только тогда, когда существует последовательность входящих многоугольников (В) и полследовательность (О) таких, что S(B)→S; S(О)→S
Теорема:
Если функция f
непрерывна и неотрицательна на [a;b]
то соответствующая ей криволинейная
трапеция квадрируема => существует
S(f)
=
 --- I
--- I
Док-во:
По условию f
непрерывна на [a;b]
=> интеграл I
от неё существует, разобьем отрезок
[a;b]
на n-равных
частей т.е.
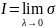 Дробл.
Дробл.
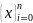 на n
равных частей =>
на n
равных частей =>
 ;
;
 – наименьшее значение функции;
– наименьшее значение функции;
(Bn)
– фигура, образованная из прямоугольников
у которых i-ая
высота равняется
 ,
тогда эта фигура будет многоугольником,
причем входящим, т.е.
,
тогда эта фигура будет многоугольником,
причем входящим, т.е.


Аналогично,
если мы в качестве
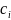 будем выбирать ту, которая
будем выбирать ту, которая
 будет наибольшим значением на i-ом
отрезке.
будет наибольшим значением на i-ом
отрезке.
 по
критерию кв. I=S(Ф)
по
критерию кв. I=S(Ф)
Замечание 1. Если f на [a;b] кусочно непрерывна и ограничена, то вывод остается прежним.

Если фигура (Ф) может быть получена за счет объединения и вычитания конечного количества более простых квадрируемых фигур, то она тоже квадрируема.


27. Понятие кубируемости и объема тел. Первый критерий кубируемости. Объем прямого кругового цилиндра.
(Т) – ограниченное тело в R3
 (M1)=(B),
(M2)=(O)
(M1)=(B),
(M2)=(O)


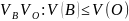


Определение.
(Т) – называется кубируемой, если его
нижний объем равен верхнему объему
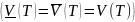
Критерий кубируемости
(T)
– кубируема <=>
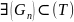 ,
,


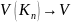
Факт.
Прямой
круговой цилиндр кубируем (Vцил)= r2h
r2h
________________________ 28. Второй критерий кубируемости: тело f кубируемло ⇔когда его границы сигма от f есть множество нулевого объема. Свойства кубируемых тел: 1) Объем v(f) любого кубируемого тела f неотрицателен. 2) Пусть f1 и f2 кубируемые тела. Если f1 содержит f2, то v(f1)≤v(f2). 3) Если тело f=f1 ∪ f2, где f1,f2 кубируемые тела, не имеющие общих внутренних точек, то f – кубируемое тело и v(f)=v(f1)+v(f2). 4) Если f1 и f2 – кубируемые тела и f=f1 ∩ f2 , то f –кубируемое тело.
_________________________________
