1) (Критерий монотонности функции, имеющей производную на интервале).

Пусть функция f принадлежащая C((a;b))непрерывна на (a,b), и имеет в

каждой точке x принадлежащей (a,b) производную f'(x). Тогда:

а) f возрастает на (a,b) тогда и только тогда, когда для любых

x принадлежащих (a,b),f'(x)≥0;

б) f убывает на (a,b) тогда и только тогда, когда для любых

x принадлежащих (a,b),f'(x)≤0.

2) (Достаточное условие строгой монотонности функции, имеющей

производную на интервале).Пусть функция f принадлежащая C((a;b))

непрерывна на (a,b), и имеет в каждой точке x принадлежащей (a,b)

производную f'(x). Тогда:

а) если для любых x принадлежащих (a,b),f'(x)>0,то f строго возрастает

на (a,b);

б) если для любых x принадлежащих (a,b),f'(x)<0,то f строго убывает

на (a,b).

3) (Критерий строгой монотонности функции, имеющей производную на

интервале) Пусть функция f принадлежащая C((a;b)),и всюду на интервале

определена производная f'(x). Тогда f строго возрастает на интервале (a,b)

тогда и только тогда, когда выполнены следующие два условия:

а) Для любых x принадлежащих (a;b),f'(x)≥0;

б) Для любого (c;d) из (a;b) существует x принадлежащий (c;d),f'(x)>0.

Аналогично, f строго убывает на интервале (a,b) тогда и только тогда,

когда выполнены следующие два условия:

а) Для любых x принадлежащих (a;b),f'(x)≤0;

б) Для любого (c;d) из (a;b) существует x принадлежащий (c;d),f'(x)<0.

Билет №5 Понятие экстр.необход.усл-е.

1опред. Если F’(x)<0 ∀x∈( - , )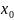

F’(x)>0 ∀x∈ , + )

Из этого => -точка минимума

2опред. Если F’(x)>0 ∀x∈( - , )

F’(x)<0 ∀x∈ , + )

Из этого => -точка максимума.

Если функция f диф-я в некоторой окрестности точки =>она непререрывна.

Док-во:

1. ∢ Точку X∈( - , )

f-диф-я на (x; ),f-непрерывна на концах в т.x, }=>по теор лангранжа ∃ ∈(x; )

F( )-F(x)=F’( )*( -x)<0

F( )<f(x) (1)

∢ точку x∈ , + )

f-диф-я на (x; ),f-непрерывна на концах в т.x, }=>по теор лангранжа ∃ ∈(x; )

F(x)-F( )=F’( )*(x- )>0

F(x)>f( ) (2) значит из (1)и(2)=> -точка минимума.

Док-во можно провести используя достаточное возр.и убывание.

Если знак произв-ой слева и справа одинак то

Если т -не будет точкой непрерывности,то выводы делать нельзя.

Максимум и миним ф-и наз-ся экстремумы ф-й.Точка в которой ф-я имеет минимум или максимум,наз-ся точка экстремума

Теорема(необходимое условие экстремума)

Если ф-я f(x) в т. ∈(a;b) имеет экстремум и в этой точке сущесвует производная равная нулю.

(По теореме ферма)

Достаточное условие экстремума.Если при переходе(слева на право),через критическую точку производная меняет знак с+ на- то в точке функция имеет максимум,а если с- на + то минимум.

Если поизводная<0,то она убывает,а если>0 то возрастает.

Если знак не меняется,то нет экстремума.

Билет №7Понятие асимптоты кривой вида асимптоты и способы их отыскания.

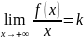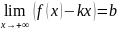Определение: Асимтота-прямая наз-ся асимтотой к кривой L если вып-ся : Если при удалении т М вдали по кривой в бесконечность величина d(М) стремится к нулю. Вертикальные ассимтоты; прямая x= явл-ся вертик.ассимптотой если хотя бы один из односторонних пределов f в точке =бесконечности. Наклонная асимптота: и это формулы для нах-я накл. Асим. Горизонтальная асимтота: Если расстояние b от точки М до кривой y=b стремится к нулю при неограниченном удалении т. М от начала координат(вправо и влево) то прямая y=b-есть гориз-я ассимтота.

Билет№6.Понятия выпуклости функции и точки перегиба.

Теоремы о выпуклости и перегибе.

Непрерывная функция y=f(x) называются выпуклой вверх на отрезке

[a,b], если для любых точек x1 и x2 отрезка [a,b] выполняется

неравенство : f((x1+x2)/2)≥(f(x1)+f(x2))/2.

При этом если неравенство строгое, то функцию называют строго

выпуклой вверх на отрезке [a,b].

Непрерывная функция y=f(x) называются выпуклой вниз на отрезке

[a,b], если для любых точек x1 и x2 отрезка [a,b] выполняется

неравенство : f((x1+x2)/2)≤(f(x1)+f(x2))/2.

Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках

интервала (a; b) вторая производная функции y = f(x) отрицательная,

т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же

f''(x) > 0 – вогнутый.

Доказательство. Предположим для определенности, что f''(x) < 0

и докажем, что график функции будет выпуклым.

Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой