
- •2).Неопределенности вида (∞/∞),(0*∞),(∞-∞).Вторая теорема
- •1) (Критерий монотонности функции, имеющей производную на интервале).
- •2) (Достаточное условие строгой монотонности функции, имеющей
- •3) (Критерий строгой монотонности функции, имеющей производную на
- •1. ∢ Точку X∈( - , )
- •X0 принадлежащий (a; b) и проведем через точку m0 касательную.
- •1.Вычисление s плоской фигуры
- •2.Задача о вычисление пути прямолинейного движения
- •30. Понятие спрямляемой кривой. Вычисление длины гладкой прямой.
- •33. Общая схема применения определенного интеграла в физике. Примеры.
- •35.Поняти несобственного интеграла 2-го рода. Свойства. Признаки сходимости.
- •25. Понятие квадрируемости и площади плоской фигуры. Критерий квадрируемости. Свойства квадрируемых фигур.
- •26. Квадрируемость и вычисление площади криволинейной трапеции. Следствия из основной формулы.
- •27. Понятие кубируемости и объема тел. Первый критерий кубируемости. Объем прямого кругового цилиндра.
1.Вычисление s плоской фигуры
Определение: криволинейная трапеция-множество точек плоскости ,
Таких что абцисса берутся из [a, b], а ордината неотрицательна и ≤f(x).
{(x
y)
∈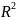 a≤x≤b
0≤y≤f(x)
}
);
a≤x≤b
0≤y≤f(x)
}
);
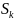 -
площадь прямоугольника ,
-
площадь прямоугольника ,
 -площадь
полоски.
≈
=(
-площадь
полоски.
≈
=(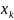 -
-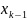 )*f(
)*f(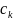 )=
f(
)*∆
)=
f(
)*∆
S=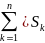 =
=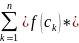 f(
)*∆
⟹S=
f(
)*∆
⟹S=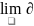
ℓ=max{ } 1≤x≤n
2.Задача о вычисление пути прямолинейного движения
материальной точки когда известна функция V
V=V(t) a≤t≤b S-?
Пусть дана f(x) и задана на [a, b] , раз отрезка [a, b] называется набор
чисел
следующего вида
 :
a=
≤
<
<
:
a=
≤
<
<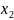 <…<
<
<b=
<…<
<
<b= (строго
возр.)
(строго
возр.)
тогда ℓ=max{∆ } 1≤x≤n .
Интегральной суммой Римана функции f называется
∂=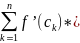 ∆
, где
∆
, где
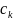 ∈[
;
],
k=1,n(1,2,
... ,n)
∈[
;
],
k=1,n(1,2,
... ,n)
Определение: Определенным интегралом функции f на [a, b]
Называется
предел вида
 (интеграл суммы сигма при λ→0)
(интеграл суммы сигма при λ→0)
если
он существует
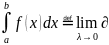
Если lim такого вида существует то фун-ия называется интегрируемой
По Риману на [a, b] f-(R) интегрируема на [a, b] .
Интеграл Римана фун-ии f численно равен S криволинейной трапеции
Если f- непрерывна и неотрицательна.
Билет №18.
Условие существования интеграла Римана:
не у всех функций существует интеграл Римана
достаточным условием существования интеграла Римана
на [a, b] является условие непрерывности на [a, b]
Необходимые условия интегрируемости по Риману ограниченность
функции на отрезке интегрирования. Доказательство: если y=f(x)
неограниченная
на [a,
b],
то она неограниченна на [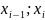 ],
т.е. на
],
т.е. на
том
отрезке можно найти такую точку
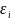 , что f
(
)*∆
, что f
(
)*∆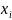 будет больше
будет больше
любого наперед заданного числа, а следовательно и интегральная сумма.
Функция
Дирихле Ѱ(x)=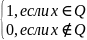
Фун-ия разрывна в каждой точке т.к. в любой точке (её окрестности)
содержиться как x∈Q так и x∉Q , то ни в одной точке нет предела,
Имеет всюду точку разрыва второго рода.
Достаточное условие: интрегрируемости- непрерывность на отрезке
Интрегрируемость функции означает существование конечного предела
последовательности интегрируемых сумм, т.е. ∀ ε>0 ∃ ∂>0 : как только разбиение
отрезка удовлетворяет неравенству max ∆ <∂ , то
│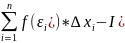 │<
ε .
│<
ε .
Классы:
Теорема 1: Непрерывные на сигменте [a, b] фун-ии интрегрируемы на
этом сигменте по Риману.
Теорема 2: Ограниченная на [a, b] фун-ия f(x), имеющая конечное число
точек разрыва, интрегрируема.на этом сигменте. В частности кусочно
непрерывная на [a, b] фун-ия интегрируема.
Теорема 3: монотонная на сигменте [a, b] фун-ия f(x) интегрируема по
Риману на этом отрезке.
Билет №19 Арифметические свойства определенного интеграла.
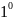 .
f-
интегрируема на [a,
b],
c∈R⟹
c
f
–интегрируема и
.
f-
интегрируема на [a,
b],
c∈R⟹
c
f
–интегрируема и
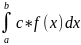 =c
=c . Доказательство:
если
c=0
то
. Доказательство:
если
c=0
то
∃
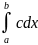 =c(b-a)
, с≠0 с>0 по условию ∀
ε>0 ∃
∂>0 ∀ λ>∂⟹│∂-I│<
ε
=c(b-a)
, с≠0 с>0 по условию ∀
ε>0 ∃
∂>0 ∀ λ>∂⟹│∂-I│<
ε
ε>0 ∃ ∂>0 λ<∂ ⟹ │∂-I│< ε/c
∢
интегрируемую
сумму функций
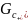 =
=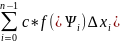 =…=c*∂
=…=c*∂
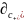 →c*I
, при λ→0
∀
ε>0 пусть ∂ из (x)
∀ λ<∂
│c*∂-c*I│<
ε
ЧТД.
→c*I
, при λ→0
∀
ε>0 пусть ∂ из (x)
∀ λ<∂
│c*∂-c*I│<
ε
ЧТД.
 .
Если фун-ия f
и g
интегрируемы по Риману на [a,
b],
то интеграл
.
Если фун-ия f
и g
интегрируемы по Риману на [a,
b],
то интеграл
от суммы этих фун-ий на [a, b] равен сумме интегралов т.е.
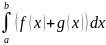 =
= +
+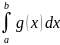 ∃
на [a,
b]
Доказательство:
∃
на [a,
b]
Доказательство:
∢
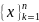 -дробн.
[a,
b]
∈[
;
]
∀
x∈
-дробн.
[a,
b]
∈[
;
]
∀
x∈ ,n
,n
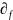 =
=
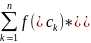 ∆
∆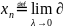
→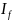 (при
λ→0)
(при
λ→0)
 →
→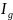 (при λ→0) ∢
(при λ→0) ∢
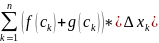 =
=
=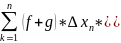 →
→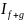 Аддетивность интервалов
Аддетивность интервалов
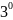 .
Следствие Если f
и g
интегрируемы по Риману то
.
Следствие Если f
и g
интегрируемы по Риману то
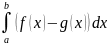 =
+
=
+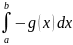 =
-
=
-
Субстрактивость.
 .
a<c<b
и фун-ия f-интегрируема
по Риману на [a,
c]
и [c,
b]
⟹
.
a<c<b
и фун-ия f-интегрируема
по Риману на [a,
c]
и [c,
b]
⟹
⟹
f-(R)
интегрируема на [a,
b],
=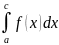 +
+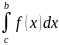
Действительно будучи интегрируемым на отрезках [a, c] и [c, b]
Фун-ия f по определению ,ограничена на них, значит и на [a, b]
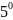 .
Если фун-ия f-(R)
интегр. на [a,
b]
и f
≥0 на [a,
b]
то
≥0
.
Если фун-ия f-(R)
интегр. на [a,
b]
и f
≥0 на [a,
b]
то
≥0
Доказательство:
∂=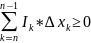 т.к.
т.к.
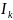 ≥0
и
≥0
и
 ≥0
≥0
- длина частич-х отрезков
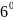 .
f,
g-(R)
интегрируемы на [a,
b]
f(x)≤g(x)
∀
x
на [a,
b]
.
f,
g-(R)
интегрируемы на [a,
b]
f(x)≤g(x)
∀
x
на [a,
b]
≤ Доказательство: из условия следует что
g
–f
≥ 0 g
и f-(R)
интегрир. по
⟹
 ≥0 по свойству
≥0 по свойству
⟹
 -
-
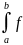
Билет №20.Теорема о среднем для определенного интеграла. Ее геометрический смысл.
f и g – непрерывны на [a;b]
f(x)
≤g(x)
∀x∈[a;b],тогда
(x)
dx
≤
(x)
dx
/
-
=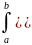 g-f)
≥0
g-f)
≥0
Следствие : Если функция f – обладает неравенством m≤f(x) ≤M ∀x∈[a;b],
f- непрерывна, тогда m (b-a) ≤ (x) dx ≤ M(b-a)
Теорема: если функция f – непрерывна на [a;b]=> ∃c∈[a;b], для которого
Выполняется следующее равенство (x) dx = f(c)(b-a)
Доказательство: По теореме Веерштрасса непрерывная функция f имеет
на [a;b] свои наименьшее и наибольшие значения
m-наименьшее значение на f на [a;b], ⟹
M- наибольшее значение на f на [a;b], ⟹
⟹m
≤
f(x) ≤ m ∀x∈[a;b]
⟹m(a-b)
≤
(x)
dx ≤ M(b-a)>0
⟹m
≤
(x)
dx
 b-a)=
Ṃ
≤
M ⟹
b-a)=
Ṃ
≤
M ⟹
по теореме о промежуточных значениях ∃ c∈[a;b]:f(c) = Ṃ⟹
⟹ (подставим f(c)= Υ и поделим на a-b). ЧТД
Геометрический смысл: Если функция непрерывна на [a;b] то найдется точка С
такая что S прямоугольнка высотой f(c) и шириной b-a будет равна S криволинейной трапеции
Интеграл = S трапеции ,S прямоугольника = (b-a)f(c)
Билет №21. Интеграл с переменным верхним пределом. Основная теорема интегрального исчисления.
1.Когда a=b (x) dx = 0
2.a > b ⟹ (x) dx ≝ - (x) dx
3.
 a<b y=f(x) непрерывна
на
[a;b],x∈(a;b]
a<b y=f(x) непрерывна
на
[a;b],x∈(a;b]
[a;x]
⊂[a;b]
⟹∃
(t)
dx =Ф(x)
Ф(a)=0
y= Ф(x),
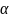 ∈[a;b]
∈[a;b]
Теорема: основная теорема интегрального исчисления) т.Барро
Если
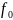 непрерывна на [a;b],то
∃
Ф’(x)
и она равна f(x)
∀x∈(a;b)
непрерывна на [a;b],то
∃
Ф’(x)
и она равна f(x)
∀x∈(a;b)
Доказательство: Ф(x)- интеграл с переменным верхним пределом
∢
∈(a;b)
По определению производной Ф’(
)=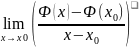 =f(
)
=f(
)
∢x< (правостороннее произведение)
В
этом случае
 =
=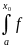 (t)
dt
-
(t)
dt
-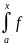 (t)
dx
x-x0
=
(t)
dx
x-x0
=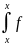 (t)
dt
x-x0
= f(cx)(x-
)
x-
=
(t)
dt
x-x0
= f(cx)(x-
)
x-
=
=f(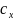 ),
где
≤
≤
x
),
где
≤
≤
x
Тогда
x--->
⟹
--->
⟹f(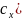 --->f(
)
--->f(
)
Ф’(x0’)= =
f(
’)
ЧТД
=
f(
’)
ЧТД
Пример:
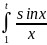 dx|
dx| =sint
=sint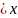
№22.Формула Ньютона-Лейбница и ее значение.
Теорема: Если y=f(x) – непрерывна на[a;b] и F(x)-первообразная для f
на [a;b],то (x) dx = F(b) - F(a).
Доказательство: По основной теореме интеграла исчисления (т.Барроу)
Ф’(x’)=f(x) ∀x∈[a;b] ⟹y=Ф(x) – первообразная для F на [a;b] ⟹по теореме о первообразной
∃с=ℝ
Ф(x)=F(x)+c
∀x∈[a;b],
если
x= 0⟹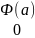 =F(a)+c
⟹c=-F(a)
=F(a)+c
⟹c=-F(a)
x=b⟹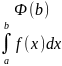 =F(b)+(-
F(a)) ЧТД
=F(b)+(-
F(a)) ЧТД
Пример: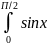 dx =-cos|
dx =-cos|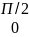 =-cos П/2-(-cos0)=1
=-cos П/2-(-cos0)=1
Замечание: Нельзя применять формулу Н-Л если условие непрерывности функции f (или условие
быть первообразной) нарушается хотя бы в одной точке [a;b]
Эта формула позволяет сводить нахождение определителя интеграла непрерывной функции
к нахождению ее первообразной.
______________________ Билет №23.Метод интегрирования по частям в определенном интеграле.
Теорема:
Если функции u(x’)
и v(x’)
имеют на на
[a;b]
непрерывные производные⟹
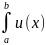 v’(x)
dx
=u(x)v(x)
|
v’(x)
dx
=u(x)v(x)
| -
-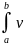 (x)u’(x)
dx
)
(x)u’(x)
dx
)
Доказательство: В силу данных условий функции u(x) и v’(x) и v(x)u’(x) – непрерывна на [a;b] ⟹
⟹ интегралы Риммана от них ⟹по правилу дифферинцирования
(uv)’=u’v+uv’ ∀x∈[a;b] ⟹y=u(x)v(x) – первообразная для функции u’v+uv’ на[a;b]
По
теореме Н-Л
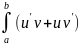 dx
= u(x)v(x)
|
dx
= u(x)v(x)
|
H’-непрерывна по условию на [a;b] ⟹ u-непрерывна на [a;b] ⟹
V’-непрерывна по условию на [a;b] ⟹ v-непрерывна на [a;b] ⟹
⟹u’v и v’u – непрерывны как производные непрерывны на [a;b] ⟹
⟹∃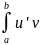 ,
,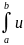 v’⟹
v’⟹
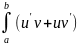 dx
=
dx
=
 dx
+
v’)
dx=uv)
|
⟹
)
dx
+
v’)
dx=uv)
|
⟹
)
Пример:
 =
= n=lnx
n’=1/x
v’=1
v=x
=xlnx
|
n=lnx
n’=1/x
v’=1
v=x
=xlnx
|
 -
- =e’lne-1ln1-x
|
=e-(1-1)=1
=e’lne-1ln1-x
|
=e-(1-1)=1
Билет №24.Метод подстановки в определенном интеграле.
Теорема:
функция y=f(x)
непрерывна на [a;b],а
x=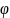 (t)
имеет непрерывную производную
(t)
имеет непрерывную производную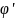 (t)
на
[
;
(t)
на
[
;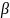 ]
]
(
)=a
(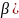 =b
(t)
∈[
=b
(t)
∈[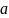 ;
;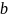 ]
∀t∈[
;
]
(x)
dx =
]
∀t∈[
;
]
(x)
dx =
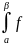 (
(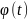 )
dt
)
dt
Доказательство: F-первообразная для f[ ; ] ⟹ левая часть =F(b)-F(a)
∢y=F(
)
первообразная для правой части (
F(
))’=F’(x)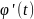 =f(x)
=f(
)
=f(x)
=f(
)
По
формуле Н-Л правая часть =F(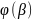 )
b)-
F(
)
b)-
F(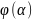 )
a)=F(b)-F(a)=
левая часть ЧТД
)
a)=F(b)-F(a)=
левая часть ЧТД
Пример: a>0
 dx
=
x=sint
0≤ t ≤
dx
=
x=sint
0≤ t ≤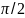 =
=
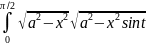 acost dt=
acost dt=
x(0)=0,x( =0,x([0;
])
=0,x([0;
]) [0;0]
[0;0]
x’=acost (непр-ая) ) ∀t∈[0;
=
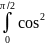 t
dt =
(n-1)
t
dt =
(n-1) =
=
