
- •Высказывания. Логические операции над высказываниями. Сложные высказывания. Таблицы истинности. Тождественно истинные и тождественно ложные высказывания.
- •Интерпритации логики высказываний. Истинность и ложность формул в интерпритации.
- •Выводимость формул f→ f и ⌐f → (f → f'). Теорема о дедукции и ее следствие.
- •Теорема дедукции:
- •Доказательство.
- •Закон контрапозиции:
- •Машины Тьюринга. Основные понятия. Задачи, разрешимые в машинах Тьюринга. Тезис Тьюринга-Черча. Функции, вычислимые по Тьюрингу. Композиция машин Тьюринга.
Машины Тьюринга. Основные понятия. Задачи, разрешимые в машинах Тьюринга. Тезис Тьюринга-Черча. Функции, вычислимые по Тьюрингу. Композиция машин Тьюринга.
Машина Тьюринга так же, как и конечный автомат, является дискретным устройством преобразования информации. Приведём её точное определение, а затем интерпретацию её работы.
Машиной Тьюринга называется частичное отображение (множество состояний)
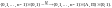
Где
 обозначает “лево”, “право”. Тот факт,
что отображение
частичное, означает, что
может быть определено не для всех
наборов аргументов. Машина Тьюринга
работает с бесконечной в обе стороны
лентой, разбитой на ячейки, в каждой из
которых написан один из символов 0, 1.
Считывающая головка машины обозревает
в каждый момент времени одну из ячеек
и за один такт, сменяющий два
последовательных момента времени,
может перемещаться влево или вправо.
Машина Тьюринга в каждый момент времени
находится в одном из состояний
обозначает “лево”, “право”. Тот факт,
что отображение
частичное, означает, что
может быть определено не для всех
наборов аргументов. Машина Тьюринга
работает с бесконечной в обе стороны
лентой, разбитой на ячейки, в каждой из
которых написан один из символов 0, 1.
Считывающая головка машины обозревает
в каждый момент времени одну из ячеек
и за один такт, сменяющий два
последовательных момента времени,
может перемещаться влево или вправо.
Машина Тьюринга в каждый момент времени
находится в одном из состояний
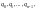 а в следующий момент времени переходит
в другое состояние или остаётся в том
же. Кроме того, машина может изменять
символ, стоящий в обозреваемой ячейке.
Все эти преобразования – изменение
состояния, информация на ленте,
направление движения полностью
определяются отображением
а в следующий момент времени переходит
в другое состояние или остаётся в том
же. Кроме того, машина может изменять
символ, стоящий в обозреваемой ячейке.
Все эти преобразования – изменение
состояния, информация на ленте,
направление движения полностью
определяются отображением
 А именно, если
А именно, если
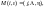 то в случае, когда машина находится в
состоянии
то в случае, когда машина находится в
состоянии
 а на обозреваемой в данный момент ячейке
написан символ
а на обозреваемой в данный момент ячейке
написан символ
 машина должна записать в эту ячейку
машина должна записать в эту ячейку
 вместо
вместо
 перейти в состояние
перейти в состояние
 и сдвинуться на одну ячейку влево.
Например, равенство
и сдвинуться на одну ячейку влево.
Например, равенство
 означает, что, находясь в состоянии
означает, что, находясь в состоянии
 и обозревая ячейку, в которой написан
символ 1, машина должна сохранить в этой
ячейке символ 1, сдвинуться вправо и
перейти в состояние
и обозревая ячейку, в которой написан
символ 1, машина должна сохранить в этой
ячейке символ 1, сдвинуться вправо и
перейти в состояние
 Если же
Если же
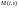 не определено, то машина, находясь в
состоянии
не определено, то машина, находясь в
состоянии
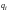 и обозревая ячейку с символом
и обозревая ячейку с символом
 прекращает работу, не изменяя своего
состояния, информации на ленте и никуда
не сдвигаясь.
прекращает работу, не изменяя своего
состояния, информации на ленте и никуда
не сдвигаясь.
Более
удобна запись программы,
которая заключает в себе всю информацию
о работе машины (таким образом, задания
машины с помощью отображения и с помощью
программы эквивалентны между собой).
Опишем составление программы. Для
каждого равенства вида
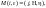 где
где
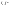 номера состояний,
номера состояний,
 направление движения, а
направление движения, а
 символы на ленте, запишем строку
символы на ленте, запишем строку
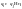 и назовём её командой.
Совокупность всех команд – это и есть
программа. Если
и назовём её командой.
Совокупность всех команд – это и есть
программа. Если
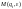 не определено, то в программе нет ни
одной команды, начинающейся с
не определено, то в программе нет ни
одной команды, начинающейся с
 Кроме того, для любых
Кроме того, для любых
 в программе есть не более одной команды,
начинающейся с
в программе есть не более одной команды,
начинающейся с

Будем
говорить, что машина
Тьюринга
 вычисляет функцию
вычисляет функцию
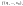 если для любого набора
если для любого набора
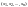 натуральных чисел машина
натуральных чисел машина
 находясь в состоянии
находясь в состоянии
 и обозревая крайнюю левую единицу в
и обозревая крайнюю левую единицу в
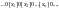 (причём [xi]=i+1
единиц, как и значение f
)останавливается в том и только в том
случае, когда значение
(причём [xi]=i+1
единиц, как и значение f
)останавливается в том и только в том
случае, когда значение
 определено, и в конце работы ленте
должно быть записано ...0
определено, и в конце работы ленте
должно быть записано ...0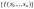 0...,
а считывающая головка машины должна
стоять напротив крайней левой единицы.
0...,
а считывающая головка машины должна
стоять напротив крайней левой единицы.
Таким
образом, если, например,
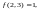 то мы должны иметь
то мы должны иметь
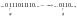
а
если
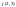 не существует, то машина, запущенная
на ленте
не существует, то машина, запущенная
на ленте
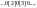 должна работать бесконечно долго (при
условии, что начальное состояние
должна работать бесконечно долго (при
условии, что начальное состояние
 а обозреваемая в начальный момент
времени ячейка – крайняя левая единица.
а обозреваемая в начальный момент
времени ячейка – крайняя левая единица.
Если
информация на ленте не имеет вид
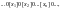 или начальное состояние не
или начальное состояние не
 или обозреваемая ячейка – не крайняя
левая единица, то поведение машины
может быть каким угодно.
или обозреваемая ячейка – не крайняя
левая единица, то поведение машины
может быть каким угодно.
Рекурсивные
функции. Напомним,
что в этой главе множество N
натуральных чисел содержит 0, т.е.
 Будем рассматривать функции (возможно,
частичные)
Будем рассматривать функции (возможно,
частичные)
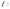
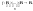 Таким образом, если
Таким образом, если
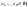 то либо
то либо
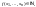 либо
либо
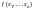 не определено. Введём в рассмотрение
простейшие
функции о
не определено. Введём в рассмотрение
простейшие
функции о s
s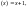 I
I
Эти ф-ции могут быть вычислены с помощью соотв. механического устройства (например, на м. Тьюринга). Определим операторы, кот. по одной или неск-ким заданным функциям строят новые ф-ции.
Оператор
суперпозиции.
Пусть даны функция
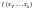 от
от
 переменных и
функций
переменных и
функций
 от
от
 переменных.. Суперпозицией функций
переменных.. Суперпозицией функций
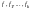 называется функция
называется функция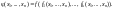
Мы
говорим, что функция
 получается применением оператора
суперпозиции
получается применением оператора
суперпозиции
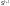 к функциям
к функциям
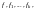 и пишем
и пишем
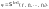
Например,
 (s,o)
– это функция
(s,o)
– это функция
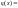 s(o
s(o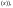 т.е. функция, тождественно равная 1, а
т.е. функция, тождественно равная 1, а
 (s,s)
– это функция
(s,s)
– это функция
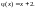
Оператор
примитивной рекурсии.
Пусть даны функции
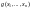 и
и
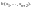 Построим функцию
Построим функцию
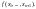 Пусть зафиксированы значения
Пусть зафиксированы значения
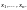 Тогда положим:
Тогда положим:
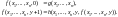
Эти равенства
определяют функцию
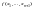 однозначно. Функция
однозначно. Функция
 называется функцией, полученной с
помощью оператора
называется функцией, полученной с
помощью оператора
 примитивной рекурсии. Используется
запись
примитивной рекурсии. Используется
запись
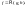
Индуктивное
определение функции (продемонстрированное
в операторе примитивной рекурсии) в
математике не редкость. Например,
индуктивно определяются степень с
натуральным показателем:

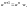 факториал:
факториал:

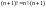 и т.д.
и т.д.
Функции,
которые могут быть получены из простейших
о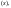 s
s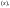 I
I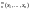 применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
применением конечного числа раз
операторов суперпозиции и примитивной
рекурсии, называются примитивно
рекурсивными.
(примитивно рекурсивные функции всюду
определен, т.е.
определены для всех значений их
аргументов). Существенно более широким
классом функций, чем примитивно
рекурсивные функции, является класс
рекурсивных
функций (определение см. ниже). В
литературе эти функции называют также
частично
рекурсивными.
Для их определения введём ещё один
оператор.
Оператор
минимизации.
Пусть дана функция
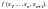 Зафиксируем какие-либо значения
Зафиксируем какие-либо значения
 первых
первых
 переменных и будем вычислять
переменных и будем вычислять
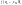
 и т.д. Если
и т.д. Если
 наименьшее натуральное число, для
которого
наименьшее натуральное число, для
которого
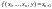 (т.е. значения
(т.е. значения
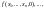
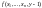 все существуют и не равны
все существуют и не равны
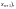 то полагаем
то полагаем
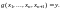 Таким образом,
Таким образом,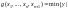
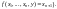
Если
такого
 нет, то считаем, что
нет, то считаем, что
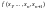 не определено. Итак, возможны три случая:
не определено. Итак, возможны три случая:
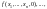
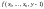 существуют и не
равны
существуют и не
равны
 а
а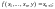
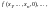 существуют и не
равны
существуют и не
равны
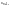 а
а
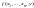 не существует;
не существует;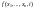 существуют при
всех
существуют при
всех
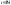 и отличны от
и отличны от
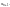
Если
имеет место 1-й случай, то
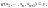 а если 2-й или 3-й, то
а если 2-й или 3-й, то
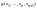 не определено. Про функцию
не определено. Про функцию
 полученную таким образом, говорят, что
она получена из
полученную таким образом, говорят, что
она получена из
 применением оператора минимизации
применением оператора минимизации
 Мы пишем
Мы пишем
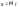
Оператор
минимизации – это очевидное обобщение
оператора взятия обратной функции.
Обобщение довольно глубокое, так как
от функции
 не требуется, чтобы она была взаимно
однозначной (по переменной
не требуется, чтобы она была взаимно
однозначной (по переменной
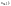
Функции,
которые могут быть получены из простейших
о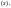 s
s I
I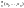 применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
Рекурсивные функции отражают наше
интуитивное представление о функциях,
вычислимых некоторым механическим
устройством. В частности, они вычислимы
на машинах Тьюринга (см. предыдущий
раздел). Наоборот, всякая функция,
вычислимая на машине Тьюринга, рекурсивна.
В предыдущем разделе, впрочем, были
построены машины Тьюринга, реализующие
функции o
применением конечного числа раз
операторов суперпозиции, примитивной
рекурсии и минимизации, называются
рекурсивными.
Рекурсивные функции отражают наше
интуитивное представление о функциях,
вычислимых некоторым механическим
устройством. В частности, они вычислимы
на машинах Тьюринга (см. предыдущий
раздел). Наоборот, всякая функция,
вычислимая на машине Тьюринга, рекурсивна.
В предыдущем разделе, впрочем, были
построены машины Тьюринга, реализующие
функции o s
s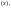 I
I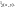 С другой стороны, не всякая функция
натуральных аргументов и даже не всякая
функция одного аргумента является
рекурсивной,. В самом деле, рекурсивных
функций имеется лишь счётное число
(т.е. их можно занумеровать натуральными
числами), а все функции
С другой стороны, не всякая функция
натуральных аргументов и даже не всякая
функция одного аргумента является
рекурсивной,. В самом деле, рекурсивных
функций имеется лишь счётное число
(т.е. их можно занумеровать натуральными
числами), а все функции
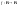 образуют несчётное множество.
Существование нерекурсивных функций
и является “математической причиной”
наличия алгоритмически неразрешимых
задач.
образуют несчётное множество.
Существование нерекурсивных функций
и является “математической причиной”
наличия алгоритмически неразрешимых
задач.
Альтернативный 19.
Проблема
самоприменимости
заключается в проверке для каждой
программы Π с входной переменной x и
выходной переменной y того, остановится
ли Π на собственном номере nΠ,
т.е в вычислении всюду определенной
функции![]()
Теорема 10.4. Проблема самоприменимости алгоритмически неразрешима, т.е. не существует структурированной программы, вычисляющей функцию Fs(x).
Доказательство
от противного. Предположим, что существует
программа P, вычисляющая функцию Fs(x).
Без ограничения общности, можно считать,
что ее выходная переменная есть y
(почему?) и поэтому ΦP,y(x)=Fs(x)
для всех x. Пусть переменная z не входит
в P. Рассмотрим следующую программу P’:
![]()
Легко
проверить, что если P на входе x выдает
результат y=1, то P’ на этом входе не
останавливается, а если P выдает результат
y=0, то P’ останавливается ( и тоже выдает
0). Пусть n’=nP’
- номер программы P’. Чему тогда равно
значение ΦP,y(n’)?
Если оно равно 1, то на входе x=n’ программа
P’ не остановится, т.е. ΦP’,y(n’)=
∞, но тогда Fs(n’)=0
![]() ΦP,y (n’). Если
же ΦP,y (n’)=0, то
P’ на входе x=n’ останавливается с
результатом 0, т.е. ΦP’,y(n’)
< ∞. Но тогда Fs(n’)=1
ΦP,y (n’)=0. Во
всех случаях получили, что Fs
ΦP,y и,
следовательно, предположение о
существовании программы для вычисления
функции Fs
неверно.
ΦP,y (n’). Если
же ΦP,y (n’)=0, то
P’ на входе x=n’ останавливается с
результатом 0, т.е. ΦP’,y(n’)
< ∞. Но тогда Fs(n’)=1
ΦP,y (n’)=0. Во
всех случаях получили, что Fs
ΦP,y и,
следовательно, предположение о
существовании программы для вычисления
функции Fs
неверно.
Заметим, что на самом деле мы доказали отсутствие структурированной программы для вычисления функции Fs. Но тезис Тьюринга-Черча и эквивалентность структурированных программ машинам Тьюринга и ч.р.ф. позволяют сделать вывод об алгоритмической неразрешимости рассматриваемой проблемы.
Альтернативный
20. Проблема
остановки (применимости):
по произвольной структурированной
программе Π определить завершится ли
вычисление Π на входе 0, т.е вычислить
всюду определенную функцию![]()
В
более общем виде проблема останова
состоит в вычислении следующей функции:
![]()
Из этого определения следует, что программа Πn останавливается на входе a тогда и только тогда, когда
выше
Операции суперпозиций, примитивной рекурсии и минимизации. Примитивно рекурсивные, частично рекурсивные и общерекурсивные функции. Тождественность частично рекурсивных функций и функций, вычислимых по Тьюрингу.
См билет 18
