
- •Высказывания. Логические операции над высказываниями. Сложные высказывания. Таблицы истинности. Тождественно истинные и тождественно ложные высказывания.
- •Интерпритации логики высказываний. Истинность и ложность формул в интерпритации.
- •Выводимость формул f→ f и ⌐f → (f → f'). Теорема о дедукции и ее следствие.
- •Теорема дедукции:
- •Доказательство.
- •Закон контрапозиции:
- •Машины Тьюринга. Основные понятия. Задачи, разрешимые в машинах Тьюринга. Тезис Тьюринга-Черча. Функции, вычислимые по Тьюрингу. Композиция машин Тьюринга.
Высказывания. Логические операции над высказываниями. Сложные высказывания. Таблицы истинности. Тождественно истинные и тождественно ложные высказывания.
Логическое высказывание — повествовательное предложение, которое формализует некоторое выражение мысли. Это утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами.
Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание. Пример: A(x) = «В городе x идет дождь.» A — высказывательная форма, x — объект.
Высказывание обычно имеет только одно логическое значение. Так, например, «Париж — столица Франции» — высказывание, а «На улице идет дождь» — не высказывание. Аналогично, «5>3» — высказывание, а «2+3» — не высказывание.
Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.
Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.
Логическая связка — это любая логическая операция над высказыванием. Например, употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если… , то», «тогда и только тогда» являются логическими связками.
Элементарные логические высказывания — это высказывания не относящиеся к составным.
Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».
Основные операции над логическими высказываниями
Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.
Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных (Законы де Моргана) .
Формула является тождественно ложной, если она ложна при любых значениях входящих в неё переменных
Если две формулы А и В “одновременно”, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Таблица истинности — это таблица, описывающая логическую функцию.
Формулы логики высказываний. Принцип индукции для них. Теорема об единственности прочтения.
Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемаяиндуктивно следующим образом:
Если P — пропозициональная переменная, то P — формула.
Если A — формула, то
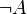 — формула.
— формула.Если A и B — формулы, то
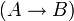 ,
,
 и
и
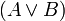 — формулы.
— формулы.Других соглашений нет.
Знаки
![]() и
и
![]() (отрицание, конъюнкция,
дизъюнкция
и импликация)
называются пропозициональными
связками.
Подформулой
называется часть формулы, сама являющаяся
формулой. Собственной
подформулой
называется подформула, не совпадающая
со всей формулой.
(отрицание, конъюнкция,
дизъюнкция
и импликация)
называются пропозициональными
связками.
Подформулой
называется часть формулы, сама являющаяся
формулой. Собственной
подформулой
называется подформула, не совпадающая
со всей формулой.
Лемма
1. Если
 и
и
 – формулы и
– начало
– формулы и
– начало
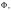 то
то
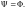
Теорема
1(о единственност прочтения(представления)).
Всякая неатомарная формула
единственным образом представима в
одном из следующих видов:

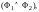
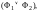
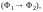 где
где
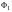 и
и
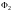 – формулы.
– формулы.
Доказательство.
Существование такого представления
следует из определения формулы. Надо
лишь доказать единственность. Понятно,
что если
представима в виде
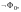 то её нельзя представить в виде
то её нельзя представить в виде
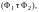 и надо лишь применить предположение
индукции к формуле
и надо лишь применить предположение
индукции к формуле
 Пусть
представима в виде
Пусть
представима в виде
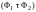 неоднозначно. Тогда
неоднозначно. Тогда
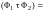
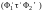 Одна из формул
Одна из формул
 является началом другой. Значит, по
лемме 1
является началом другой. Значит, по
лемме 1
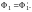 Но тогда
Но тогда
 и
и
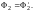 Это доказывает единственность.
Это доказывает единственность.
Следствие.
Пусть
– формула ИВ. Тогда с каждым вхождением
символа
 или символа
или символа
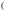 в эту формулу однозначно связывается
вхождение в
подформулы, начинающейся с этого
символа. Доказательство. Действительно,
если в
есть символ
в эту формулу однозначно связывается
вхождение в
подформулы, начинающейся с этого
символа. Доказательство. Действительно,
если в
есть символ
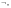 то при построении формулы
ранее была построена формула
то при построении формулы
ранее была построена формула
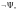 начинающаяся с этого символа, причём
– тоже формула. Формула
начинающаяся с этого символа, причём
– тоже формула. Формула
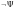 как раз и является подформулой,
начинающейся с данного вхождения
символа
как раз и является подформулой,
начинающейся с данного вхождения
символа
 Единственность следует из леммы 1.
Аналогично разбираются случаи вхождения
в
символа (.
Единственность следует из леммы 1.
Аналогично разбираются случаи вхождения
в
символа (.
