3. Интерпритации логики высказываний. Истинность и ложность формул в интерпритации.

Символы л,и (``ложь'', ``истина'') называются истиностными значениями. Интерпретация пропозициональной сигнатуры  есть функция из  в {л,и}.

Если  конечна, тогда интерпретация может быть определена таблицей её значений, например:

p q л и

(3)

Семантика логики высказываний определяет какие истиностные значения назначены формуле F интерпретацией I.

Прежде всего нам надо связать функцию с каждой пропозициональной связкой – функцию из {л,и} в {л,и} с унарной связкой ¬ и функцию из {л,и} {л,и} в {л,и} с каждой бинарной связкой. Функции определяются следующими таблицами:

x ¬(x) л и и л x y &(x, y) (x, y) (x, y) л л л л и л и л и и и л л и л и и и и и

Для любой формулы F и любой интерпретации I истиностное значение F^I , назначенное формуле F интерпретацией I, определяется как значение суперпозиции соответствующих булевых функций, а именно, следующим образом:

• F^I = I(F) если F – атом,

• (¬F )^I = ¬(F^I),

• (F  G)^I = (F^I,G^I) для каждой бинарной связки .

Заметим, что это определение рекурсивно: (¬F)^I определяется через F^I и (F  G)^I – через F^I и G^I.

Если F^I = I(F), то формула F истинна при интерпретации I

(символически I |= F ).

4. Деревья истинности. Теоремы о корректности и полноте.

5. Исчисление высказываний. Аксиомы и правило вывода. Вывод. Вывод из системы гипотез. Свойства выводимости.

Каковы бы ни были формулы А, В, С, следующие формулы называют аксиомами исчисления высказываний:

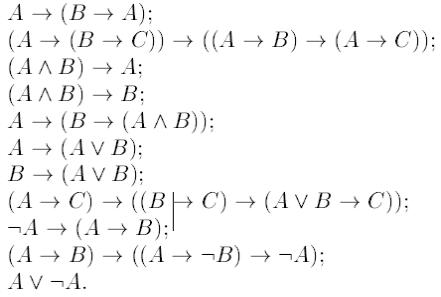
Выводом в исчислении высказываний называется конечная последовательность формул, каждая из которых есть аксиома или получается из предыдущих по правилу вывода. Это правило разрешает получить (вывести) из формул А и (А → В) формулу В.

Пусть Г — некоторе множество гипотез, каждая из которых является аксиомой или выводится из предыдущих по правилу вывода. Тогда формула А выводима из Г, если существует вывод из Г, в котором она является последней формулой.

Свойства выводимости:

Пусть G - некоторое множество формул данной теории, A, В и C - произ-вольные формулы той же теории. Рассмотрим некоторые свойства выводимо-сти в формальных аксиоматических теориях.

1. Если G содержится в некотором множестве формул F и если G ├ A, то F ├ A. Доказательство. Пусть A имеет вывод А1,А2,...,Аn (1) из гипотез G. Если некоторая формула Аi принадлежит G, то, очевидно, Аi ∈ F. Следовательно, вывод (1) формулы А является выводом формулы А из гипотез F. Что и требовалось доказать. 2. G ├ A тогда и только тогда, когда в G существует конечное подмноже-ство Н такое, что Н ├ А. Доказательство следует из определения вывода. 3. Пусть G ├ A и каждая формула В, принадлежащая G, выводима из не-которого множества формул F, тогда F ├ A. Доказательство. Пусть A имеет вывод А1,А2,...,Аn (2) из гипотез G. По определению вывода некоторые Аi из (2) могут принадлежать G, но каждая формула из G, имеет вывод из F. Заменим в (2) все Аi, принадле-жащие G, выводом Ai из F. В результате получим последовательность формул: B1,B2,...,Bm, которая уже является выводом А из F. Что и требовалось доказать. Как частный случай п.3 имеем: 3` . Если A ├ B и B ├ C, то А ├ C. 4. Если G,A ├ B и G ├ A, то G ├ B. Доказательство. Пусть B имеет вывод B1,B2,...,Bn (3) из гипотез G и А, а формула А имеет вывод А1,А2,...,Аm (4) из гипотез G. В выводе (3) формулы В некоторые из Вi могут быть равны А. Заменим такие Вi последовательностью (4). В результате получим последова-тельность формул C1,C2,...,Cr, которая является выводом для В из гипотез G. Что и требовалось доказать.