Закон контрапозиции:

;

Законы поглощения:

1)  ;

2)  ;

Законы дистрибутивности:

1)  ;

2)  .

14. Эквивалентные преобразования в логике предикатов. Приведенные формулы. Теорема о существовании эквивалентной приведенной формулы. Нормальные формулы. Теорема о существовании эквивалентной нрмальньй формулы.

Пусть P есть формула, содержащая свободную переменную x. Пусть Q есть формула, которая не содержит переменной x. Тогда следующие пары эквивалентных формул являются законами эквивалентных преобразований логики предикатов:

1. (""x) P(x)ÚЪ Q=(""x) (P(x)ÚЪ Q);

2. (""x) P(x)ÙЩ Q=(""x) (P(x)ÙЩQ);

3. ($$x) P(x)ÚЪ Q=($$x) (P(x)ÚЪ Q);

4. ($$x) P(x)ÙЩ Q=($$x) (P(x)ÙЩQ);

5. ØШ((""x) P(x))=( $$x) (ØШP(x));

6. ØШ(($$x) P(x))=( ""x) (ØШP(x));

7. (""x) P(x)ÙЩ (""x) Q(x)=(""x) (P(x)ÙЩQ(x));

8. ($$x) P(x)ÚЪ ($$x) Q(x)=($$x) (P(x)ÚЪ Q(x));

Правила 7 и 8 называются правилами выноса кванторов, которые позволяют распределять квантор всеобщности и квантор существования по операциям конъюнкции и дизъюнкции соответственно.

Формула а называется приведённой формой если а не ссодержит операций импликации и эквиваленции и знаки отрицания относятся лишь к элементарным формулам. Например: ∃x¬P(x,y)&Q(z))˅A, ¬S˅P(x), ∃xQ¬(x)

Теорема: Всякая формула алгебры предикатов равносильна некоторой приведённой форме.

Док-во:Пусть а – произвольная формула алгебры предикатов. Проведём док-во индукцией по количеству n операций в формуле а. Если n = 0, то а – элементанрая формула и => а является приведённой формой.

Пусть n > 0 и для всякого k, 0 ≤ k ≤ n, формулы, содержащие k логических операций равносильны приведённой форме.

Формула а называется предварённой нормальной формой, если а имеет вид: а=Q₁x₁Q₂x₂…Q_nx_nb, где Q₁…Q_n – кванторы, а формула b является приведённой формой, не содержащей кванторов.

Теорема: Всякая формула а алгебры предикатов равносильна некоторой предварённой нормальной форме.

15. 1

16. Исчисление предикатов. Аксиомы. Правила вывода. Выводимые формулы. Тождественная истинность аксиом. ||||Предикат – высказываемая функция, определенная на некотором множестве M, то есть такая n-местная функция P, которая каждому упорядоченному набору <a1,a2,…,an> элементов множества M сопоставляет некоторое высказывание, обозначаемое P(a1,a2,…,an); P называется n-местным предикатом над M. Под 0-местным предикатом понимается произвольное высказывание.

Обычно высказывание с его истинностным значением 1 (И) или 0 (Л). При это предикат получает определение:

n-местным предикатом на множестве M называется произвольная n-местная функция, определенная на M и принимающая значения 0 или 1.

Если на наборе значений аргументов <a1,a2,…,an­> предикат P принимает значение 1, то есть P(a1,a2,…,an)=1, то говорят, что этот набор значений аргументов удовлетворяет предикату P, а предикат выполняется для набора <a1,a2,…,an>.

Алфавит исчисления предикатов содержит 4 группы символов:

Предикатные переменные – выражения вида 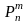, где m и n – неотрицательные числа;

1. Предметные переменные x1,x2,…;

2. Логические символы & (конъюнкция), V (дизъюнкция), ¬ (отрицание), ≡ (эквивалентность), ⇒ (импликация), 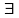(квантор существования), 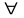(квантор общности);

3. Вспомогательные символы «(« и «)», а так же «,».

Более сложные конструкции определяются индуктивно:

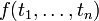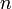• Терм есть символ переменной, либо имеет вид , где — функциональный символ арности , а 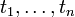— термы.

• Атом имеет вид , где 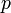— предикатный символ арности , а — термы.

• Элементарной формулой называется всякая пропозициональная переменная, а так же любое выражение вида P(y1,y2,…,ym­), где P – m-местная предикатная переменная (m>0), а(y1,y2,…,ym­) – произвольные предметные переменные. Из элементарных формул строятся предикатные формулы по следующим правилам:

1. всякая элементарная формула есть формула;

2. Если P и Q – формулы, то ¬P, (P&Q), (P V Q), (P ⇒ Q) – формулы

3. Если P – формула и x – предметная переменная, то 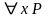P и 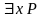P - формулы.

Исчисление предикатов — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов.

Два правильно вывода:

(П1) из A и A⇒ B следует B

(П2) из A следует

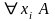
Некоторые выводимые формулы:

1. 

2. 

3. 

4. 

5. 

6. 

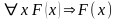
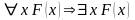
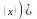
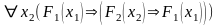
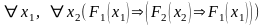
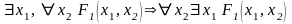7. Аксиомы исчисления предикатов разбиваются на 2 класса: логические аксиомы и собственные или нелогические аксиомы.

Логическими являются следующими аксиомы:

(А1)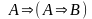

(A2)

(A3)

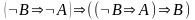
(A4) 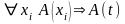, где t – терм, свободный для переменной 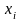в формуле

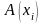
(А5) 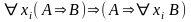, если в формуле A не содержится свободных вхождений переменной

17. Тождественная истинность формул, выводимых в исчислении предикатов. Теорема о полноте для исчисления предикатов (без доказательства). Пример вывода формулы в исчислении предикатов.

18. Алгоритмическая неразрешимость проблемы самоприменимости.

Теорема 8. Существует перечислимое неразрешимое множество натуральных чисел.

Доказательство. Рассмотрим вычислимую функцию, не имеющую вычислимого всюду определённого продолжения. Докажем, что её область определения будет искомым множеством. В самом деле, по теореме 1 (Пусть – подмножество множества натуральных чисел (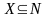 ). Тогда следующие условия эквивалентны: (1) множество перечислимо; (2) есть область определения некоторой вычислимой функции; (3) есть множество значений некоторой вычислимой функции.)

множество перечислимо. Если бы было разрешимым, то функция

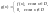
была бы вычислимым всюду определённым продолжением функции Противоречие.

Будем говорить, что для машины Тьюринга проблема остановки алгоритмически разрешима, если существует другая машина Тьюринга которая для каждого натурального числа выясняет, остановится или не остановится машина имея на входе число Для определённости пусть имея на входе число выдаёт на выходе 1, если останавливается (будучи запущенной на ленте, на которой написано число и выдаёт на выходе 0, если не останавливается.

Теорема 9. Существует машина Тьюринга для которой проблема остановки алгоритмически неразрешима.

Доказательство. Возьмём вычислимую 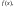функцию не имеющую всюду определённого вычислимого продолжения (такая функция существует по теореме 7: Существует вычислимая функция, не имеющая всюду определённого вычислимого продолжения.). По теореме 8 её область определения является неразрешимым множеством. Пусть – машина Тьюринга, вычисляющая функцию Тогда проблема остановки машины является алгоритмически неразрешимой задачей.