
- •39. Условный экстремум функции многих переменных. Определения. Примеры.
- •40. Условный экстремум с ограничениями типа равенств. Необходимые условия экстремума первого и второго порядка. Пример.
- •41. Условный экстремум с ограничениями типа равенств. Достаточные условия экстремума. Пример.
- •42. Условный экстремум с ограничениями типа неравенств. Необходимые условия экстремума первого и второго порядка. Пример.
- •43. Условный экстремум с ограничениями типа неравенств. Достаточные условия экстремума первого и второго порядка. Пример.
- •44. Линейное программирование. Задачи об использовании ресурсов. Графический метод решения.
39. Условный экстремум функции многих переменных. Определения. Примеры.
Пусть
даны дважды непрерывно дифференцируемая
целевая функция
 и функции ограничений
и функции ограничений
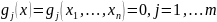 ,
определяющие множество допустимых
решений U.
,
определяющие множество допустимых
решений U.
Требуется
исследовать функцию
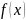 на экстремум, т.е. определить точки
на экстремум, т.е. определить точки
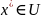 ее локальных минимумов и максимумов
ее локальных минимумов и максимумов
 ,
где
,
где
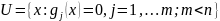 .
.
Функция
 называется обобщенной функцией Лагранжа,
числа
называется обобщенной функцией Лагранжа,
числа
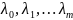 − множителями Лагранжа. Классической
функцией Лагранжа называется функция
− множителями Лагранжа. Классической
функцией Лагранжа называется функция
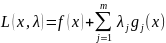 .
.
Градиентами
обобщенной и классической функций
Лагранжа по x
называются вектор-столбцы,
составленные из соответствующих частных
производных первого порядка по
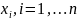 .
.
Вторым
дифференциалом обобщенной (классической)
функции Лагранжа
называется функция
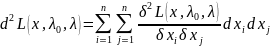 (
(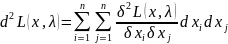 ).
).
Первым
дифференциалом ограничения называется
функция
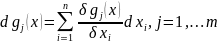
40. Условный экстремум с ограничениями типа равенств. Необходимые условия экстремума первого и второго порядка. Пример.
Необходимые
условия экстремума первого порядка.
Пусть − точка локального экстремума в
задаче. Тогда найдутся числа
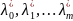 ,
не равные одновременно нулю и такие,
что выполняются следующие условия:
,
не равные одновременно нулю и такие,
что выполняются следующие условия:
стационарности обобщенной функции Лагранжа по x
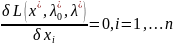 или
или
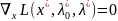 ;
;
допустимости решения
 .
.
Точки
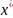 ,
удовлетворяющие системе при некоторых
,
удовлетворяющие системе при некоторых
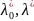 ,
называются условно-стационарными.
,
называются условно-стационарными.
При
решении задач проверка регулярности
затруднена, так как точка
заранее неизвестна. Поэтому, как правило,
рассматриваются два случая:
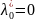 и
и
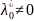 .
Если
,
в системе полагают
.
Если
,
в системе полагают
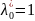 .
Это эквивалентно делению системы
уравнений на
.
Это эквивалентно делению системы
уравнений на
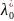 и замене
и замене
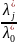 на
на
 .
При этом обобщенная функция Лагранжа
становится классической.
.
При этом обобщенная функция Лагранжа
становится классической.
Точка экстремума, удовлетворяющая системе при , называется регулярной, а при − нерегулярной.
Необходимые
условия экстремума второго порядка.
Пусть
− регулярная точка минимума (максимума)
в задаче и имеется решение
 системы. Тогда второй дифференциал
классической функции Лагранжа, вычисленный
в точке
,
неотрицателен (неположителен):
системы. Тогда второй дифференциал
классической функции Лагранжа, вычисленный
в точке
,
неотрицателен (неположителен):
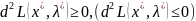 для всех таких, что
для всех таких, что
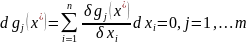
41. Условный экстремум с ограничениями типа равенств. Достаточные условия экстремума. Пример.
Достаточные
условия экстремума. Пусть имеется
точка
,
удовлетворяющая системе. Если в этой
точке
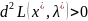 ,
(соответственно,
,
(соответственно,
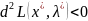 )
для всех ненулевых таких, что
,
то точка является точкой локального
минимума (максимума) задачи экстремума.
)
для всех ненулевых таких, что
,
то точка является точкой локального
минимума (максимума) задачи экстремума.
Достаточные и необходимые условия экстремума второго порядка проверяются в условно-стационарных точках, которые удовлетворяют системе при или системе, так как для практики представляет интерес случай, когда в функции Лагранжа присутствует целевая функция, экстремум которой ищется.
Алгоритм решения задачи следующий.
Шаг 1. Составить обобщенную функцию Лагранжа
Шаг 2. Записать необходимые условия экстремума первого порядка а) б)
Шаг 3. Решить систему для двух случаев
1)
2) (при этом поделить условие а) на и заменить на )
В результате найти условно-стационарные точки выделив из них полученные при (они могут быть регулярными точками экстремума).
Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума:
а) записать выражение для второго дифференциала классической функции Лагранжа в точке :
б) записать систему дополнительных условий в точке :
в)
из последних условий выразить любые из
m дифференциалов
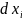 через остальные (n-m)
и подставить в
через остальные (n-m)
и подставить в
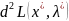 ;
;
г)
если
при
ненулевых
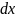 ,
то в точке
− условный локальный минимум. Если
при ненулевых
,
то в точке
− условный локальный максимум. Если
достаточные условия экстремума не
выполняются, следует проверить выполнение
необходимых условий второго порядка,
следуя аналогичной процедуре. Если они
выполняются, то требуется дополнительное
исследование, в противном случае в точке
нет условного экстремума.
,
то в точке
− условный локальный минимум. Если
при ненулевых
,
то в точке
− условный локальный максимум. Если
достаточные условия экстремума не
выполняются, следует проверить выполнение
необходимых условий второго порядка,
следуя аналогичной процедуре. Если они
выполняются, то требуется дополнительное
исследование, в противном случае в точке
нет условного экстремума.
Шаг 5. Вычислить значения функции в точках условного экстремума.
Приведем в виде таблицы результаты исследования на наличие в точке локальных экстремумов при соблюдении необходимых условий первого порядка
причем .
