17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.

Пусть прост-во элемент событий – ограниченная область в n-мерном прост-ве. Назовём мерой области её длину, если n=1; площадь, если n=2; и объём, если n=3.

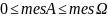
Рассмотрим случайный эксперимент, состоящий в броске точки в область , число исходов несчётно. Будем считать, что исходы равномерно распределены в области , т.е. вер-ти попадания точки в произвольное подмножество пропорциональны объёму объёму этого подмножества. Это говорит о равновозможности исходов. Рассм. событие A ; мера: Определение: геометрической вер-тью события А называется величина: P(A)=

Статистическое: в большом классе событий вер-ть нельзя вычислить или с помощью классического определения вер-ти или с пом. геометрического определения вер-ти, т.к. исходы в них не равновозможны. Для таких событий, обладающих св-вом устойчивости частот и св-вом массовости, применимо статистическое определение вер-ти. Определение: за вер-ть события А в статистическом смысле принимается относительная частота события А в достаточно большом числе опытов n:

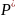(A)= , n – число опытов, -частота появления события А. Плюсы определения: оно универсально, применимо к любым случайным экспериментам. Минусы: 1) требует большого числа опытов,2) Лишь примерно равно точной вероятности, т.к. в другой серии из n опытов вер-ть (A) может быть совсем другой.

18.Сложение вероятностей несовместных событий: вер-ть появления хотя бы одного из двух несовместных событий (AB=Ф) равна сумме вер-тей этих событий, т.е.:P(A+B)=P(A)+P(B). Следствие: вер-ть появления хотя бы одного из n попарно несовместных событий, равна сумме вер-тей этих событий: .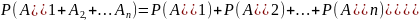

_{Сложение} вероятностей совместных событий: вер-ть появления хотя бы одного из двух совместных событий (AB ) равна сумме вер-тей этих событий без вер-ти их совместного появления: P(A+B)=P(A)+P(B)-P(AB). Док-во: пусть А и В – совместны, т.е. AB , представим событие (A+B) в виде суммы трёх несовместных вариантов:

(1), A= -несовм, P(A)=P( , т.к. в правой части (1) представлены несовместные события, то 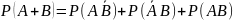, в эту ф-лу подставим значения и , получим:

P(A+B)=P(A)-P(AB)+P(B)-P(AB)+P(AB), т.е. P(A+B)=P(A)-P(AB)+P(B), Ч.Т.Д.

Эту теорему можно обобщит для любого числа событий: P(A+B+C)= P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC), а для n событий теорема выглядит так:P(

19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.

В практических задачах события обычно взаимосвязаны. Если о событии В ничего не известно, то P(A)= - безусловная вероятность. Но если известно, что событие В уже произошло, и требуется вычислить вер-ть события А, то в качестве пространства элементарных событий следует взять событие В; т.е.B= , тогда событию А будут благоприятствовать исходы изAB=A’. Тогда новая вер-ть события А будет вычисляться по ф-ле:P(A’)=P(A|B)= = = . Определение: условной вер-тью события А, при условии, что событие В уже произошло, называется величина.P(AB)=

Теоремы умножения: 1. Вер-ть совместного появления двух событий равна произведению вероятности одного из на условную вер-ть другого, при условии, что первое событие уже произошло: P(AB)=P(A) P(B|A)= P(B) P(A|B)

2. Вероятности появления нескольких событий равна произведению вер-ти одного из них на соответствующие условные вер-ти остальных событий: P(

20. Опред: Соб А наз независимым от соб В,если его вер-ть не зав-т от того произошло соб А или нет. Р(А|В)=Р(А).Если Р(А|В) Р(А),то соб А и В наз завис-ми.Утвержд:св-во зав-ти и незав-ти соб-й взаимно,т.е если А зав-т от В,то и В не зав-т от А,и наоборот. Док-во: пусть А не зав-т от В,т.е Р(А/В)=Р(А).По Т.(умнож. вер-тей) запишем: Р(АВ)=Р(А)Р(В/А)+Р(В)Р(А/В),т.к А не зав-т от В,то Р(В/А)=Р(В),т.е В не зав-т от А ч.т.д.Можно дать друг опред: соб А и В наз незав-ми, если появление одного из них не меняет вер-ти появл другого.Св-ва незав соб-й:1)Т.(умножение незав соб-й):вер-ть совм появл 2-х незав соб-й=произвед вер-тей этих соб-й,т.е Р(А/В)=Р(А)Р(В) 2)если соб А и В незав-мы,то будут незав-ми и след соб-я

Док-во:докажем,что если А и В нез-мы,то будут нез-мы и А и В’; А=А =А(В+ )=АВ+А (несов)

Р(А)=Р(АВ)+Р(А . Т.о Р(А -незав-мы. Ч.т.д.

3)Если соб А незав от соб В₁ и В₂,а В₁ и В₂ явл-ся несовместн,то А незав от соб В= В₁ + В₂

Док-во: Р(А(В₁ + В₂))=Р(А В₁ + АВ₂)=

Р(А В₁)+Р(АВ₂)=Р(А)Р(В₁)+Р(А)Р(В₂)=Р(А)(Р(В₁) + Р(В₂))=Р(А)Р(В₁ + В₂)=Р(А)(В)=>А,В-незав.Ч,т.д 4)Когда рассм >2-х соб-й,то попарн незав-ть может и не означать незав-ть по совок-ти

О пред:А₁, …А_n-незав по совокупности,если Р(А₁, …А_n)=Р(А₁)Р(А₂) …Р(А_n)

2 1)Пусть соб А может наступить при появл одного из соб:Н₁,Н₂, …Н_n.Будем наз-ть соб Н₁,Н₂, …Н_n-гипотезами.Р(Н_i)-вер-ти гипотез.Р(А/ Н_i)-усл вер-ть соб А при гипотезе Н_i. Гипотезы должны удовл-ть след усл:1)Н₁+Н₂+…+Н_n= 2)HiHj= . i=jпопарно несовм,т.е гипотезы обаз-т полн группу соб.При вып-и этих усл-й будет вып-ся . Будем искать безуслов вер-ть соб А: А=А = ;

P(A)= = ; -ф-ла полной вер-ти.

Туристы вышли из пункта П1,выбирая наудачу одну из дорог.Какова вер-ть,что они придут в пункт П2.

А-туристы попали в пункт П2. Н_i-выбрали i-дорогу, i=

P(A)= = = ; В случае если А уже произошло,то первонач вер-ти гипотез подлежат переоценке.Найдедем усл вер-ть -Ф-ла Бейса. Она позволяет изменить первонач(априорные) вер-ти гипотез на апостериорные при усл,что соб А уже произошло.

22) Сл.вел-это числ ф-я,кот в рез-те сл.эксп-та принемает различ знач-я.Обозначается X,Y,Z,… одно из возм зн-й случ вел-н X,Y,Z.ПР:опыт-бросание игр кости. Сл вел Х-число выпавших очков. Х={1,2,3,4,5,6}-мн-во знач-1 сл.вел-н конечно.

Сл/вел мн-во знач-й кот-х конечно или счетно наз ДСВ. Другие сл/вел недискр-е.Формальное опред сл/в:сл/в-числ ф-я элем соб-я Х( ,опред-я в простр-ве элем соб-й, . Замеч:знач х= Х( сл/в Х есть всегда число,причем кажд число появл с опред вер-тью р( .Опред:З-ном распред сл/в Х наз любое правило(ф,таблица),позволяющ нах-ть вер-ти сл соб-й,связанных со сл/вел-ми. Если известен з-н рапред сл/в Х,то говорят,что сл/в Х распр-на по этому з-ну.Для LCD p-y распред строится в виде таблицы возмож знач-й сл/в и соотв-х вер-тей.Эта табл наз рядом распред-я:

Х	х1	х2	…	х n
р	p1	p2	…	pn

Т.к {Х=х_i), {Х=х_j), i несовм-ны и образ-т полн группу соб-й,по Т слож несовм соб-1 получаем:

23) Ф-ей распред. любой случ. величины наз. вероятность того, что она примет значение, меньше заданного аргумента х. F(x)=P(X<x) Геом. смысл ф-ии распред. Основные св-ва ф-ции распределения: 1. Ф-ция распред – неубыв. ф-я, т.е. если Док-во: Предст. собой (x<x₂) как сумма 2-х несовм. соб. ; А – н/с – В.; ; 2. Из определения как вероятность. 3. 5. Ф-ция распред. непрерывна слева, т.е. 6. Графиу ц-ии распределеия. Ф-ция может быть: а) непрерывной на некот. участках, б) постоянной -//-, в) возрастать -//-, г)иметь разрывы 1 рода (скачки)

7. Вероятность попадания в интервал. Док-во: , ч. и т.д. 8. Вероятность отдельного значения. рассмотрим нерв-о: и вычисл. lim при . . Если ф-я распределения непрерывна в т. х, то вероятн. отд. зачения случ. величины=0. Если в т. х ф-я распредел. им. скачок, то вероятн. отд. значения случ. величины = величине этого скачка в т. х. 9. , ч. и т.д. 10. аналогично д-ву св-ва 9.

24) Б. наз. случ. велич. х непрерывной, если ее ф-ция распред. непрерывна и диф-ма всюда, за ислючением, м.б., конечного числа точек. Непрерыв. случ. величина – важнейший класс недискр. случ. величин, т.к. для таких случ. величин ф-я распред. не имеет скачков, то вероят. любого отдельного знач-я случ. вел.=0. 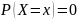. Плотность распред. вероятностей: рассмотрим механич. интерпрет. распред. вер. Пусть масса=1 непрер. размазана с некот. неравном. плотностью вдоль оси ОХ. Вероят. показ. случ. величины х на участок Δхδ интерпретируются как масса, приход. на этот участок, а сред. плотность на уч. Δх. 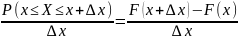Переходя здесь к lim при Δx→0 получ. значение плотности т. х. , т.к. F(x) – диф-ма. Опред.: Плот. распределения (или плотность вероятностей) непрер. случ. величины Х в т. х наз. производ. от ф-ии рспред в этой т.: f(x)=F`(x) Говорят, что случ. велич. Х распред. с плотн. f(x) или имеет распределение с плотностью f(x). Плот. распред – одна из форм з-нов распред. случ. величины. Однако, в отличие от ф-и распред. плот. вер. определна только для непрерывн. случ. величин

25) Св-ва: 1. , ч. и т.д. Аналогично наход. след. вероятности: , ч. и.т.д.; 3. т.к. F(x) – неуб. ф-ция, то 4. Условие нормировки Док-во: , ч. и т.д.

26) З-ны распред. – полные, исчерпывающие хар-ки случ. величин. Однако, не всегда требуется детальное опис. св-в случ. вел. Иногда дост. указать числов. параметры, характериз. случ. величину, такие как напр. серднее, вокруг кот. радброс. вер. значения случ. велич., величину этого разброса и др. числа. К томуже этм нахожд. з-нов распред – дов. слож. задача. Важнейщ. числ. хар-кой явл. математич. ожидание. Рассм. механим интерпрет. дискрет. случ. велич. В т. x_i сосред. массы p_i, сумм. всех масс =1. Т., характ. среднее взвешенна всей системы, явл. центром масс. Обозм. абсц. ц. масс x_c и вычислим ее. Опред.: математическим ожиданием (ср. значеним) распред. дискр. случ. велич. назыв. сумма произведений всех возм. значений случ. велич. на соотв. вероятности этих значений, т.е. (в предполож., что ряд сходится абсолютно). Если случ. велич. или счетное число знач-ий, то Если ряд расх., то гов., что случ. велич. не им. колич. мат. ожидания. Рассм. мех. интерпрет. непрерывн. случ. вел. Масса=1 непер. размазана вдоль оси ОХ с плотностью f(x). В этом случае абсцисса центра масс находится по ф-ле: Опред.: Мат. ожиднием непрерыв. случ. величины назыв. несобств интеграл (в предполю, что он вход. абс.) Свяь со ср. арифмет.: При больш. кол-ве опытов сред. арифм. набл. значений случ. вел. ~равно мат. ожид. этой случ. вел-ны. Пусть в больш. ч-ле опытов n значение x_i случ. вел. X появилось с частотой n_i. При этом . Сред. прифметическое знач. случ. величины Х найдем по ф-ям: Т.е. сред. арифм. появлений случ. величины X в n опытах=сумме произвед. значений этой случ. вел. на соотв. относит. частоты Q т.к. при большом знач-ий n тнос. част. появл. соб. ~равно вероят. этого события, то получ. что сред. арифм набл. знач. случ. вел. равно ее мат. ожиданию. Этот факт составл. содержание одной из предл. теории ТВ з-на больш. чисел.

27. Модой случайной величины называется наиболее вероятное

её значение, т.е. то, для которого вероятность Pi (для

дискретной случайно величины или плотность вероятностей

f(x) для непрерывной случ. величины) достигают максимума.

x_m- такое, что P(X=x_i)=max P(X=x_i), Если X дискретная случ. величина

x_m{ X такое, что f(x)=maxf(x), x Если X-непрер случ. вел-на.

Мода может не сущ-ть, иметь единственное знач-е(унимодальное распред), иметь множество значений

(полимодальное).Опред: медианной непрерывной случ. величины X

Называется такое значение n_x для которого выполняется

P(X<nx)= P(X>nx)=1/2.С геометрической т. зрения медиана это такое знач случ величины, при кот площади под кривой распред-я

слева и справа от него равны.

Свойства мат. oжидания

1)Мат. oжид от неслучайной величины равно этой случ вел-не

M[C]=C

M[C]=C*1=C

2) M[C+X]=CM[X] 3)M[CX]=CM[X]

28.Определение: начальным моментом порядка к случ. велич X

называется мат. ожидание случ. велич

М[ {

Из опред видно, что мат. ожид случ. вел Х яв-ся начальным моментом 1-ого порядка. Опред: центрированной случайной величиной Х наз-ся

отклонение случ вел Х от её мат ожидания.

Мат. ожид центрированной случ. величины = 0.Опред: центральным моментом порядка к случ. величины

Х наз начальный момент соответствующей центрированной

случ величины

Связь между центральным и начальным моментами.

Рассмотрим центральным момент

Для непрерывной случ. величины получаем такую же

Формулу. Аналогичные рассуждения приводят к формуле

Имеем 2-ой центральный момент или мат. ожидание от

Квадрата центрированной случ. величины.

29Определение: дисперсией случайной величины х называется

Её второй центрированный момент

D[X]=

Вычисление дисперсии:

{ Дисперсия-есть характеристика рассеивания (разброса) значений

Случ. величины вокругеё мат ожидания.

Свойства дисперсии:

1) D[C]=0

Док-во: D[C]=M[(X-C)^2]=M[0]=0

2) Если D[X+C]=D[X]

Док-во:

D[X+C]=M([X+C-M[X]-C^2])=M[(X-M[X])^2]=D[X]

3)D[CX]=M[(CX-CM[X])^2]=M[C^2(X-M[X])^2]=

C^2*M[(X-M[X])^2]=C^2*D[X]

D[CX]=C^2D[X]

4)Дисперсия от функции случайной величины

Пусть Y= , тогда D[Y]=M[(Y-M[Y])^2]=M[Y^2]-M^2[Y]=

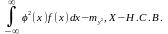
5) С механической точки зрения дисперсия-момент инерции

Относительно центра масс.

30) Для определения разброса возможных значений случ. величины

Вокруг её мат. Ожидания вводят еще одну числовую характеристику

Среднее квадратичное отклонение.

- среднее значение случайной величины

Зная числовые характеристики можно получить примерное

Представление О диапазоне возможных значений случ.

величины, а именно возможные значения случ. величины

X, с большой долей вероятности нахождения на интервале

Моменты случ. величины можно вычислять не непосредственно,

А с помощью вспомогательных функций.

Производящая функция

Производящая функция определена для дискрет. Случ. величины,

Принимающей целочисленные значения к=0,1,2…

, где 0<t<1 – параметр, а

Вычислим производную от производящей функции в т. t=1

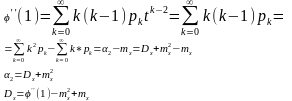
Характеристическая функция для н.с.в.

Если не существует производной n-ого порядка от харак. Функции

В нуле, то момент k-ого порядка для данной случайной величины

Неопределен.

31. Индикатор события А

Пусть вероятность того, что событие А произошло равна p

xi	0	1
pi	1-p	p

Найдем числовые характеристики этой случайной величины

Т.е. мат. Ожидание индикатора события, равна вероятности

Появления этого события

То есть дисперсия Ia равна произведению вероятностей появления

На его не появление

Функция распределения

Биноминальное распределение.

1: каждый эксперимент имеет два исхода: успех неуспех

2: вероятность успеха в каждом эксперименте одинакова и равна

р(1)=р; р(0)=1-р=q

Независимые эксперименты повторяются n раз

Утверждение: Число успехов Х в n опытах в схеме

Испытания Бернулли

Док-во: Х=m распределяется на ряд вариантов Bi, в которых

Успех происходит n раз, а неуспех n-m раз

Bi=(++-++-…++) + m штук

- n-m штук

Т.к. испытания независимы, то вероятность каждого варинта

Равна P(Bi)=

Число несовместных вариантов

По теореме сложения вероятностей получаем Bi

Для нахождения числовых характеристик составим

Производящие функции

32. В схеме независимых испытаний Бернули рассмотрим

Случайную величину Х- число безуспешных попыток до 1-ого

Успеха.(Р(Х=0)=р-первая попытка успешна.

xi	0	1	2	n
pi	p	qp	(q^2)*p	(q^n)*p

Проверим условие нормировки

Для нахождения числовых характеристик запишем производящую ф-ию

;

;

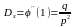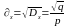
Часто рассматривается другой вид геометрического распределения

X- число опытов( сколько требуется произвести опытов до 1-ого успеха)

xi	1	2	3	n
pi	p	qp	(q^2)*p	(q^n-1)*p

Здесь Y=X+1 предыдущее распределение, сдвинутое на единицу

Найдем числовые характеристики

33. Распределение Пуассона имеет случ. величина Х

Принимающая целочисленные значения {0,1,2…}

Вероятность которых находится по формуле

P(X=m)= , а – параметр распределения

Ряд распределения

X	0	1	2	m
P

Проверим условие нормировки

Для нахождения числовых характеристик запишем

Производящую функцию

;

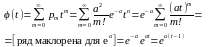
Параметры Пуассоновского распределения равны

Одновременно и мат. Ожиданию и дисперсии

Случ. величины.

Утверждение: Распределение Пуассона есть предельный

Случай биноминального распределения, когда n->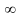

p->0, то их произведение np=а-const

док-во:

Найдем предел при n->

Следствие: распределение Пуассона с параметрами а=np можно прибли-

жено применять вмесир биноминального, когда число опытов оч. велико

(100 и более) а вероятность р очень мала.