3) Переменные (обобщенные координаты) состояния или промежуточные

переменные, задаваемые вектором обобщенных координат x

x = (x1 , x2 ,...xn )T (1.4)

Переменные многомерного объекта являются векторными величинами, зависящими от времени, а сам объект может быть структурой рис. 1.1.

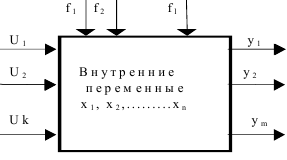
Рис.1.1

Согласно понятию векторного пространства множество всех значений, которые может принять вектор управления Uв момент времени t , образует пространство управляющих величин. Аналогично, множество всех значений, которое могут принимать векторы возмущений f , регулируемых величин y и обобщенных координат x в момент времени t , образуют пространство возмущающих воздействий, пространство регулируемых величин и пространство состояний системы.

В любой момент времени t состояние системы является функцией начального состояния x (t0) и вектора входных величин.

Вектор регулируемых величин в момент t является также функцией начального состояния x0 (t0) и вектора входных величин U(t0 ,t) и f(t0 ,t) и может быть записан как

y (t) =Ψx(t 0 ); u(t0 ,t); f(t) (1.5)

Уравнение (1.5) называют уравнением состояния системы. Для систем, описываемых дифференциальными уравнениями, уравнения могут быть записаны в следующем виде:

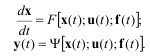(1.6)

Для линейных систем уравнения состояния сводятся к следующим:

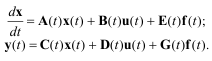(1.7)

Уравнение (1.6) и (1.7) устанавливает взаимосвязь между входными (управляющими и возмущающими) и выходными (фазовыми) координатами объекта, определяемую видом функций F[x(t);u(t);f(t)] и Ψ[x(t);u(t);f(t)], а также

позволяет описать процесс движения системы в пространстве состояний, как результат решения векторного дифференциального уравнения (1.6) или (1.7).

1.2 Понятие матрицы передаточной функции

Введение векторных переменных позволяет для линейных систем использовать привычный аппарат передаточных функций и структурных схем, однако понятие передаточной функции значительно расширяется.

Пусть имеется многомерная система управления со структурной схемой показанной на рис. 1.2. и системой дифференциальных уравнений, записанных в

символической форме.

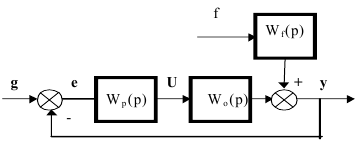
Рис.1.2

По аналогии с одномерными системами можно записать:

(1.8)

где Q(p)-квадратная матрица операторных коэффициентов размера n на n:

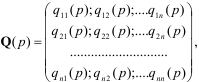
R(p)- прямоугольная матрица операторных коэффициентов размера n на k:

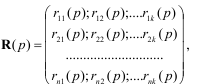
S(p)- прямоугольная матрица операторных коэффициентов размера n на l:

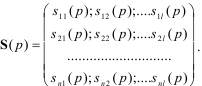
Для получения системы дифференциальных уравнений необходимо перемножить прямоугольную или квадратную матрицы на матрицы - столбцы соответствующих переменных объекта.

Взаимосвязь уравнений состояния с уравнениями системы в виде (1.8)

определяется из следующих соотношений. Из второго уравнения (1.7) выразим переменную x (t) через y(t):

(1.9)

и подставим это выражение в первое уравнение (1.7):

(1.10)

Преобразовывая по Лапласу (1.10) и группируя подобные члены, получим

выражение аналогичное (1.8), которое путем приравнивания матриц при одноименных переменных позволяет установить взаимосвязь (1.7) с (1.8).

(1.11)

где I – единичная матрица,

По аналогии с одномерными системами, используя основные правила

теории матриц, можно ввести понятие матриц передаточной функции, временных и частотных характеристик.

Если умножить (1.8) на обратную матрицу , то получим:

(1.12)

Отсюда можно получить выражение для матриц передаточных функций

системы по управлению

(1.13)

и возмущению

(1.14)

Из теории матриц известно, что обратная матрица может быть вычислена по методу неопределенных коэффициентов применительно к выражению:

где I - единичная матрица, что в конечном итоге приводит к решению систем линейных алгебраических уравнений.

Второй способ вычисления обратной матрицы задаётся выражением:

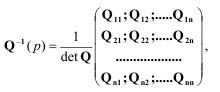(1.15)

Если в матрице передаточной функции для каждого элемента матрицы

найти обратное преобразование Лапласа, то получится матрица весовых функций (матрица Коши).

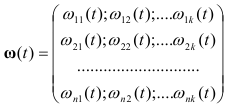(1.16)

Если в момент времени t=0 на все к входов поступают управляющие воздействия u(t), то изменение i- ой регулируемой величины может быть найдено посредством интеграла Дюамеля на основании принципа суперпозиции:

(1.17)

Аналогично одномерным системам, производя замену оператора p на оператор jω для каждого элемента матрицы передаточных функций (1.13), (1.14), получим матрицу комплексной передаточной функции.

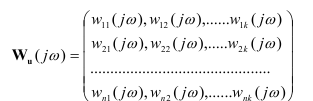(1.18)

Если теперь положить, что одновременно на все входы многомерной систе-

мы поступают гармонические сигналы одинаковой частоты ω , то АЧХ и ФЧХ i-ой регулируемой величины могут быть вычислены по следующим формулам:

Т. е. сначала определяют частотную передаточную функцию по i- ому вы-

ходу как сумму комплексных элементов j- ой строки матрицы частотной передаточной функции всей системы, а затем АЧХ и ФЧХ находят как модуль и аргумент этой суммы комплексных элементов.

Также как и для одномерных систем, в многомерных системах одной и той же матрице передаточной функции может соответствовать несколько вариантов структурных схем и уравнений состояния. Т.е. по уравнениям состояния матрица

передаточной функции может быть получена однозначно, обратное утверждение

будет неверным.