5.1. Необходимое условие экстремума

Если дифференцируемая функция достигает экстремума в точке 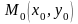, то ее частные производные первого порядка в этой точке равны нулю, т. е.

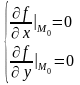(7)

Точки, в которых частные производные обращаются в нуль, называются стационарными точками. Следует заметить, что не всякая стационарная точка является точкой экстремума. Каждая их этих точек должна быть проверена на экстремум с помощью достаточных условий.

5.2. Достаточные условия экстремума

Пусть точка – стационарная точка функции .

Обозначим

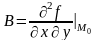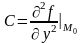; ; . (8)

Составим выражение 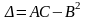. Тогда, если:

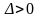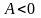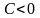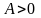1) , то функция имеет в точке экстремум, а именно максимум при (или ) и минимум при (или );

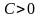2) 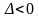, то в точке экстремума нет;

3) 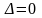, то требуются дальнейшие исследования.

Пример 8. Исследовать на экстремум функцию .

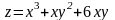Решение. Найдем частные производные первого порядка:

.

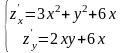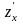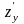Приравняем и к нулю и решим полученную систему уравнений:

.

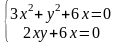Из второго уравнения , .

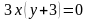
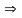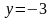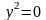
Подставим полученные уравнения в первое уравнение, имеем для 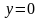. Для получаем 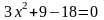или .

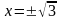Получим три точки, в которых может быть экстремум , , .

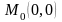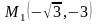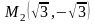Найдем 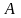, , 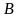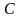по формулам (8):

, , .

, , .

, , .

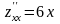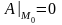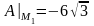
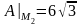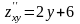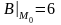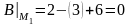
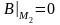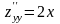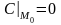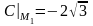
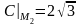Тогда 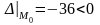– экстремума в точке – нет,

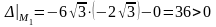– экстремум есть,

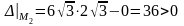– экстремум есть.

Выясним, какой экстремум в точках 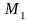и . Это определяется по знаку второй производной по переменной . И так как в точке , в ней будет максимум, а в точке , то в ней – минимум.

6. Градиент и производная по направлению

Определение 10. Градиентом функции в точке 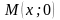называется вектор, выходящий из точки и имеющий своими координатами частные производные функции в этой точке:

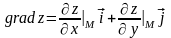. (9)

Если имеем функцию трех переменных 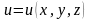, то

.

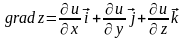Чтобы ввести понятие о производной по направлению, рассмотрим функцию в некоторой области, содержащей точку 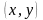и единичный вектор 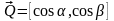любого направления.

Если функция дифференцируема в точке , тогда производная по направлению вычисляется по следующей формуле:

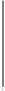
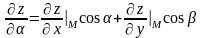. (10)

Производная по направлению характеризует

с корость изменения функции в точке

в направлении вектора 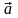. Из векторной

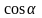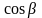алгебры известно, что и есть

направляющие косинусы вектора ,

п оэтому если 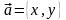, то

Рис. 3

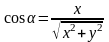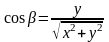; (11)

Пример 9. Найти 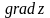в точке 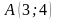и производную в точке в направлении вектора 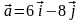, если .

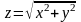Решение. Найдем частные производные функции и подсчитаем их значения в точке :

; ;

; .

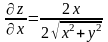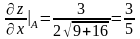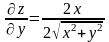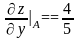По формуле (9) .

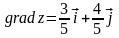Чтобы найти производную по направлению (10), найдем направляющие косинусы вектора , используя формулы (11):

, .

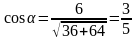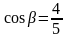Найдем производную по направлению:

,

,

.

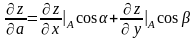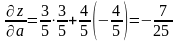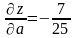7. Метод наименьших квадратов

Пусть в результате получена таблица значений функции для ряда значений независимой переменной :

				…
				…

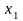
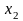
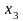
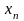
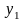
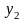
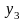
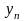
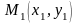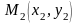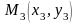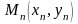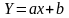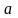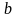Если точки , , , … , примерно располагаются на одной прямой, это означает, что зависимость между и близка к линейной: . Подберем неизвестные коэффициенты и так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.

Широко распространенным методом решения данной задачи является метод наименьших квадратов. Этот метод заключается в следующем.

Рассмотрим сумму квадратов разностей значений 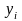, даваемых экспериментом, и функции в соответствующих точках, т. е.

.

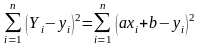Подбираем параметры и так, чтобы эта сумма имела наименьшее значение. Поскольку 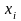и – постоянные, то указанная сумма есть функция параметров и :

.

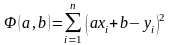Чтобы найти значения параметров и , воспользуемся необходимыми условиями экстремума функции двух переменных: найдем частные производные от 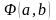по переменным и и приравниваем их к нулю:

,

.

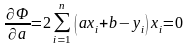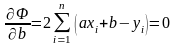Параметры и найдем из этой системы. Для этого перепишем ее в следующем виде:

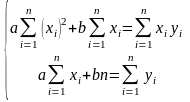(12)

Для определения чисел и получили систему двух уравнений перовой степени. Можно доказать, что эта система всегда имеет единственное решение и что для найденных чисел и функция достигает минимума. Подставляя найденные значения и в уравнение , получим линейную функцию, наилучшим образом отражающую зависимость между величинами и , полученными из опыта.

Пример 10. Полученные из опыта значения функции при различных значениях независимой переменной приведены в таблице:

(13)

	0	1	1,5	2,1	3
	2,9	6,3	7,9	10	13,2

Методом наименьших квадратов найти функцию 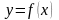в виде .

Решение. Для решения этой задачи составим таблицу.

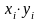
1	0	2,9	0	0
2	1,0	6,3	1	6,3
3	1,5	7,9	2,25	11,85
4	2,1	10,0	4,41	21
5	3,0	13,2	9,0	39,6
∑	7,6	40,3	16,66	78,75

Воспользуемся для нахождения параметров и системой (12), в которой ; ; ; ;

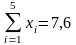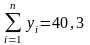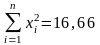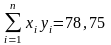получим .

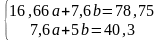Решим систему. Для этого выразим из второго уравнения:

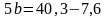
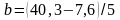
Подставим в первое уравнение:

.

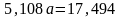
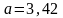Отсюда .

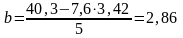Итак, , 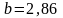, и, следовательно, искомая функция имеет вид:

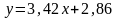. (14)

П равильность вычислений легко проверить,

сделав чертеж.

На координатной плоскости строим точки 6,22

по результатам таблицы (13) и график

полученной прямой (14). В случае верного 2,86

решения точки будут расположены близко

к прямой.

Рис. 6 – решение верно 1

Рис. 4