
- •080100.62 По направлению Экономика
- •Понятие функции двух независимых переменных
- •2. Производные функции двух независимых переменных
- •2.1. Частные производные первого порядка
- •2.2. Частные производные высших порядков
- •3. Полный дифференциал функции двух переменных
- •4. Касательная плоскость и нормаль к поверхности
- •5. Экстремум функции двух независимых переменных
- •5.1. Необходимое условие экстремума
- •5.2. Достаточные условия экстремума
- •6. Градиент и производная по направлению
- •7. Метод наименьших квадратов
- •8. Первообразная и неопределенный интеграл
- •Свойства интегралов
- •9. Методы интегрирования
- •9.1. Непосредственное интегрирование
- •9.2. Метод замены переменной (подстановки)
- •9.3. Метод интегрирования по частям
- •10. Интегрирование рациональных дробей
- •10.1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •10.2. Правильные и неправильные рациональные дроби
- •10.3. Разложение правильной дроби
- •10.4. Нахождение коэффициентов
- •10.5. Правило интегрирования рациональных дробей
- •11. Интегрирование некоторых иррациональностей
- •12. Интегрирование тригонометрических выражений
- •13. Определенный и несобственный интегралы, их вычисление
- •14. Геометрические приложения определенного интеграла
- •Из чертежа видно, что
2.2. Частные производные высших порядков
Определение 6. Частными производными второго порядка от функции называются частные производные от ее частных производных первого порядка.
Обозначаются частные производные 2-го порядка так:
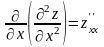 ;
; 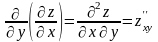 ;
;
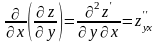 ;
; 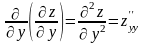 .
.
Частные
производные
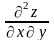 и
и
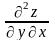 называются смешанными производными.
Можно доказать, а на практике это легко
проверить, что
называются смешанными производными.
Можно доказать, а на практике это легко
проверить, что
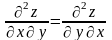 ,
если они непрерывны.
,
если они непрерывны.
Пример
4. Дана функция
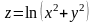 .
Найти все ее частные производные 2-го
порядка и убедиться, что
.
.
Найти все ее частные производные 2-го
порядка и убедиться, что
.
Решение.
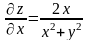 ;
; 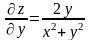 ;
;
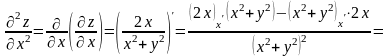
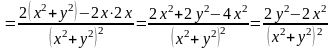 ;
;
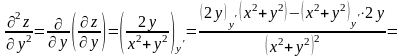
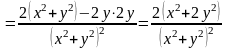 ;
;
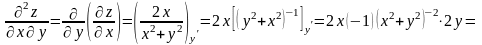
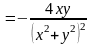 ;
;
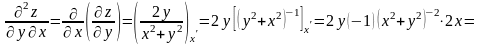
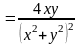 .
.
Из
последних двух равенств видно, что
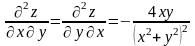 .
.
Пример
5. Показать,
что функция
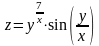 удовлетворяет уравнению
удовлетворяет уравнению
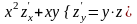 .
.
Решение.
Находим
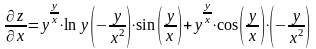 ;
;
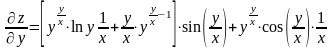 .
.
Подставим найденные значения в левую часть уравнения:
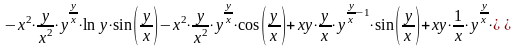
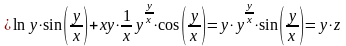 .
.
Получаем тождество, следовательно, функция удовлетворяет данному уравнению.
3. Полный дифференциал функции двух переменных
Пусть
есть функция двух независимых переменных.
Зафиксируем
,
а затем
.
Тогда по аналогии с дифференциалом
первого порядка
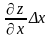 и
и
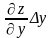 называют частными дифференциалами, а
выражение
называют частными дифференциалами, а
выражение
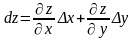 является полным дифференциалом функции
двух переменных. Положив
является полным дифференциалом функции
двух переменных. Положив
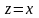 ,
получим, что
,
получим, что
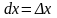 ,
а, положив
,
а, положив
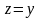 ,
получим
,
получим
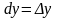 .
Формула для
.
Формула для
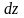 примет вид:
примет вид:
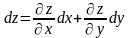 .
(2)
.
(2)
Пример 6. Найти полный дифференциал функции
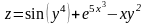 .
.
Решение. Используем формулу (2). Найдем , .
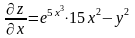 ;
; 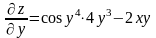 .
.
Тогда
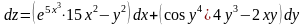 .
.
4. Касательная плоскость и нормаль к поверхности
Определение
7. Касательной
плоскостью к поверхности в точке
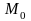 называется плоскость, содержащая в себе
все касательные к кривым, проведенным
на поверхности через точку
.
называется плоскость, содержащая в себе
все касательные к кривым, проведенным
на поверхности через точку
.
Определение 8. Нормалью к поверхности называется прямая, проходящая через точку касания и перпендикулярная касательной плоскости.
Если
поверхность задана неявно, т. е. ее
уравнение
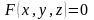 ,
тогда уравнение касательной плоскости
в точке
,
тогда уравнение касательной плоскости
в точке
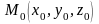 к поверхности имеет вид:
к поверхности имеет вид:
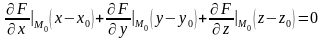 (3)
(3)
где
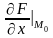 ,
,
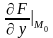 ,
,
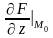 – значения частных производных функций,
вычисленных в точке
,
а
,
,
– текущие координаты точки касательной
плоскости.
– значения частных производных функций,
вычисленных в точке
,
а
,
,
– текущие координаты точки касательной
плоскости.
Уравнение нормали к поверхности в точке записывается в виде:
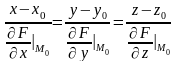 (4)
(4)
Если уравнение поверхности задано явно, т. е. , то формулы (3) и (4) примут вид:
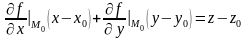 (5)
(5)
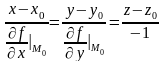 .
(6)
.
(6)
Пример
7. Написать
уравнение касательной плоскости и
нормали к поверхности
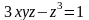 в точке
в точке
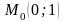 .
.
Решение.
Определим третью координату точки
касания, подставив
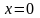 ,
,
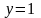 в уравнение поверхности. Получим
в уравнение поверхности. Получим
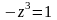 ,
откуда
,
откуда
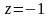 .
Таким образом, точка касания имеет
координаты
.
Таким образом, точка касания имеет
координаты
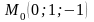 .
.
Перепишем
уравнение в виде
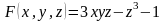 и найдем частные производные:
и найдем частные производные:
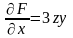 ;
; 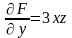 ;
; 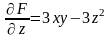 .
.
Подсчитаем их значения в точке :
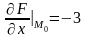 ;
; 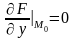 ;
; 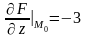 .
.
Применяя формулы (5) и (6), получим:
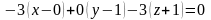 или
или
 .
.
Итак,
 – уравнение касательной плоскости,
– уравнение касательной плоскости,
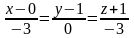 – уравнение нормали.
– уравнение нормали.
Нуль
в знаменателе означает, что направляющий
вектор нормали, а значит и сама нормаль
перпендикулярны оси
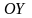 .
.
5. Экстремум функции двух независимых переменных
Определение
9. Функция
имеет в точке максимум (или минимум),
равный
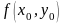 ,
если в окрестности этой точки для всех
точек
,
отличных от
,
выполняется неравенство
,
если в окрестности этой точки для всех
точек
,
отличных от
,
выполняется неравенство
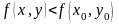 или
или
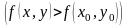 .
.
Максимум или минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума.
