§2. Формулы алгебры высказываний. Виды формул.

Пропозициональными переменными называются такие переменные, вместо которых можно подставлять конкретные высказывания. Эти переменные будем обозначать заглавными латинскими буквами: A, B, C, …, P₁, Q₁, X, Y, Z, X₁,…

Понятие формулы алгебры высказываний определяется следующим (индуктивным) образом:

а) всякая пропозициональная переменная есть формула;

б) если F₁ и F₂ – формулы, то выражения (F₁), (F₁F₂), (F₁F₂), (F₁F₂), (F₁F₂) также является формулами;

в) других формул, кроме построенных по правилам двух предыдущих пунктов, нет.

Договоримся в формулах опускать внешние скобки и все те скобки, которые становятся лишними, если логическим операциям приписать убывающие ранги в таком порядке: , , , ,.

Подформулой формулы называется всякая ее часть, которая сама является формулой.

Формула F(X₁, X₂, …X_n) называется выполнимой, если существует хотя бы один набор значений логических переменных Х₁, …, Х_n, при котором формула F(X₁, …,X_n) обращается в истинное высказывание

Формула F(X₁, X₂, …X_n) называется опровержимой, если существует хотя бы один набор значений логических переменных Х₁, …, Х_n, при котором формула F(X₁, X₂, …X_n) обращается в ложное высказывание.

Формула F(X₁, X₂, …X_n) называется тождественно ложной (или противоречием), если она обращается в ложное высказывание при любом наборе значений логических переменных.

Формула F(X₁, X₂, …X_n) называется тождественно истинной (или тавтологией, или законом логики), если она обращается в истинное высказывание при любом наборе значений логических переменных. Обозначение тавтологии: |= F(X₁, X₂, …, X_n).

Пусть дана некоторая формула F(X₁, X₂, …, X_n), и требуется найти все наборы значений логических переменных, при которых формула F принимает значение 1 (или значение 0). Будем записывать это так: F(X₁, X₂, …, X_n)=1 (F(X₁, X₂, …, X_n)=0) и говорить, что нужно решить логическое уравнение.

Упражнения.

1. Определите, является ли последовательность символов формулой:

а) ((PQ)R)R;

б) ((PQ)R)(PR);

в) ((PQ)(R(QS)));

г) ((PQ)(RS));

д) (P(QRP));

е) ((PQ)(P(RS)));

ж) ((P(QR))((PR)Q)).

2. Опустите возможно большее число скобок в следующих формулах:

а) (((P)QR)((SP)Q));

б) ((P)(Q)(S))(R);

в) ((Q)R)(S);

г) ((((P(Q))R)P)(PQ)).

3. В следующей последовательности символов всевозможными способами расставьте скобки так, чтобы получилась формула:

а) PQRS;

б) PQRPR;

в) PQR;

г) PQRQ;

д) PQRQ.

4. Вычислить значение формулы при указанных наборах значений логических переменных:

а) Q(PR(RQ)), (P,Q,R)=(0,1,1); (P,Q,R)=(0,0,0);

б) PQR (PQ)S, (P,Q,R,S)=(1,0,0,1); (P,Q,R,S)=(1,1,0,0).

5. Составьте таблицы истинности для следующих формул и определите вид формулы (тождественно истинная, тождественно ложная, выполнимая, опровержимая):

а) (PQ)((PQ)P);

б) ((PQ)P)Q;

в) (PQ)(PQP);

г) (P(QP))((QP)Q);

д) ((PQ)Q)Q;

е) ((PQ)Q)(PQ);

ж) PQRPQR;

з) R((PR)(PQ)).

6. Докажите, что следующие формулы выполнимы:

а) (PP);

б) (PQ)(QP);

в) (Q(PR))((PR)Q);

г) ((PQ)R)Q;

д) (PQ)((RQ)(QQ))

Решение:

в) Для доказательства воспользуемся определением выполнимой формулы. Необходимо найти хотя бы один набор значений логических переменных P, Q, R, при котором формула принимает значение 1. Допустим, что такой набор (P, Q, R) существует, т.е. при некоторых P, Q, R: QPR=1 и (PRQ)=1. По определению операции отрицания: PRQ=0. Тогда из таблицы истинности импликации видно, что Q=0, а PR=1. Дизъюнкция двух высказываний может принимать значение 1 в трех случаях. Выберем один из них, но так чтобы выполнялось условие, что QPR=1. Так как Q=0, то импликация независимо от PR будет равна 1. Следовательно P и R можем выбрать любые из следующих: P=0, R=1 или P=1, R=0 или P=1, R=1. Пусть P=1 и R=1.

Итак, нашелся такой набор значений логических переменных (P,Q,R)=(1,0,1), при котором формула принимает значение 1. Следовательно, по определению формула является выполнимой.

7. Докажите, что следующие формулы опровержимы:

а) ((X(YZ))(YX))Y;

б) ((XY)Z)((XY)(XZ));

в) ((XY)((YZ)(ZX)))((XY)Z);

г) (XY)(XZ)(YZ)(UV)(UW)(VW)(XU);

д) (XY)((XY)(XY)).

Решение: аналогично №2.6. Воспользоваться определением опровержимой формулы. Найти такой набор значений логических переменных, при котором формула принимает значение 0.

8. Решить логические уравнения:

а) ((PQR)(QP))Q=0;

б) P(QR)=1;

в) (PQR)(PQR)=0;

г) (PQ)(PQ)=0;

д) PPQ=1;

е) (QR)(PQPR)=0;

ж) ((PQR)(QS)SP)R=0;

з) (PQ)(QP)(PR)=0;

Решение: а) По определению импликации это уравнение равносильно системе

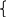( PQR)(QP)=1

Q=0

откуда

Q =1

(P1R)(0P)=1

Учитывая, что 0P=1 при любом логическом значении P и то, что (P1R)1=1 так же при любых значениях Pи R, то решением будет всякий набор значений логических переменных, в котором Q=1, а P и R – любой объект из множества {0;1}. Возможны следующие наборы:

(P, Q, R)=(1,1,1);

(P, Q, R)=(0,1,1);

(P, Q, R)=(0,1,0);

(P, Q, R)=(1,1,0).

9. Cоставив таблицы истинности, докажите, что следующие формулы являются тавтологиями:

а) PP (закон исключенного третьего);

б) (PP) (закон отрицания противоречия);

в)  PP (закон двойного отрицания);

г) PP (закон тождества);

д) (PQ)(QP) (закон контрапозиции);

е) ((PQ)(QR))(PR) (правило цепного заключения);

ж) (PQ)(PQ) (закон противоположности);

з) (PQ)(QP) (коммутативность конъюнкции);

и) (PQ)(QP) (коммутативность дизъюнкции);

к) ((PQ)R)(P(QR)) (ассоциативность конъюнкции);

л) ((PQ)R)(P(QR)) (ассоциативность дизъюнкции);

м) (P(QR))((PQ)(PR)) (дистрибутивность конъюнкции относительно дизъюнкции);

н) (P(QR))((PQ)(PR)) (дистрибутивность дизъюнкции относительно конъюнкции);

о) (PP)P (идемпотентность конъюнкции);

п) (PP)P (идемпотентность дизъюнкции);

р) (PQ)(PQ);

с) (PQ)((PQ)(QP));

т) (P(QP))P (первый закон поглощения);

у) (P(QP))P (второй закон поглощения);

ф) (PQ)(PQ) (первый закон де Моргана);

х) (PQ)(PQ) (второй закон де Моргана);

ц) (PQ)(PQ).

10. Составив таблицы истинности следующих формул, докажите, что они являются тавтологиями:

а) P(QP);

б) (PQ)((P(QR))(PR));

в) P(Q(PQ));

г) P(PQ);

д) (PQ)P;

е) (P(QR))((PQ)(PR));

ж) ((PQ)(PQ))P;

з) (PR)((QR)((PQ)R)) (эта тавтология называется «разбор случаев»);

и) (PQ)((PQ)P);

к)  PP;

л) (PQ)(QP);

м) (PQ)((QP)(PQ));

н) ((PQ)P)P;

о) (PQ)(PQ);

п) (PR)((PQ)(RQ));

р) (P(QR))(Q(PR)).

11. Докажите, что если формулы F и FG являются тавтологиями, то и формула G является тавтологией, т.е. если ╞ F, ╞FG, то╞G. (Правило вывода, называемое «модус поненс» (сокращенно MP)).

12. Докажите, что:

а) если ╞FG и ╞FH, то ╞ GH;

б) если ╞FG, ╞FH, ╞GK, то ╞HK;

в) если╞FG, ╞ GH, то ╞FH;

г) если ╞F, ╞FG, то ╞G.

Решение: в) Пусть F(X₁, …, X_n), G (X₁,…, X_n), H(X₁,…, X_n) – формулы, о которых идет речь в теореме. Предположим, что формула FH не является тавтологией. Это означает, что существуют такие конкретные высказывания A₁,…A_n, что высказывание F(А₁,…, А_n) истинно, а высказывание H(A₁,…, A_n) ложно. Тогда высказывание F(А₁,…, А_n) ложно. Далее, так как формула FG является тавтологией, то высказывание G(А₁,…, А_n) истинно. Но с другой стороны, поскольку GH – тавтология, то высказывание G(А₁,…, А_n) истинно. Получили противоречие. Следовательно, наше предположение оказалось неверным, а значит FH – тавтология.

13. Доказать методом от противного общезначимость следующих формул:

а) P(PQ);

б) P(QPQ);

в) ((PQ)(QR))(PR);

г) (PQ)(QP);

д) (PQR)(PRQ);

Р ешение: в) Пусть данная формула не общезначима, тогда должно иметь решения уравнение: ((PQ)(QR))(PR)=0. Это уравнение равносильно системе:

(PQ)(QR)=1

PR=0

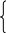
PQ=1

QR=1

PR=0

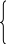
P=1

R=0

1Q=1

Q0=1

Два последних уравнения противоречат друг другу. Следовательно, наше предположение оказалось неверным, а значит формула является тавтологией.