Синтез релейно-контактных схем.

7.5. Постройте наиболее простые релейно-контактные схемы по заданным условиям работы:

а) (0,0,0)= (1,0,1)=1;

б) (1,1,0)= (0,0,0)= (1,0,0)=1;

в) (0,0,0)= (0,1,0)= (1,0,0)= (0,1,1)=1;

г) (0,0,1,1)= (1,1,1,0)= (0,1,1,0)=1;

д) (0,0,1,1)= (0,0,0,0)= (1,1,0,0)=1;

е) (1,1,1,1)= (0,1,0,1)=1.

Указание. Используя СДНФ, найдите сначала аналитическое выражение для функции . Затем максимально упростите полученное выражение для функции . После этого начертите соответствующую схему.

7.6. Каждый их трех членов бюро голосует «за», нажимая кнопку. Постройте по возможности более простую схему, через которую ток проходил бы и зажигал бы электрическую лампочку тогда и только тогда, когда не менее двух членов бюро голосуют «за».

7.7. Имеется одна лампочка в лестничном пролете двухэтажного здания. Постройте схему так, чтобы на каждом этаже своим выключателем можно было бы гасить и зажигать лампу независимо от положения другого выключателя.

7.8. Постройте релейно-контактную схему с четырьмя переключателями, которая проводит ток тогда и только тогда, когда замыкаются не все переключатели, а только некоторые из них.

7.9. Постройте схему с тремя переключателями, которая замыкается тогда и только тогда, когда замкнут либо один, либо два переключателя. При построении используйте не более шести контактов.

7.10. Постройте релейно-контактную схему из контактов x, y, z и t, которая замыкается тогда и только тогда, когда выполняются следующие условия:

а) замкнут контакт x и замкнут один из контактов y и z,

или

б) разомкнут контакт t и разомкнуты два и только два из остальных контактов,

или

в) замкнуты два и только два контакта, но контакты у и t вместе не замкнуты.

7.11. Постройте схему с пятью переключателями, которая замыкается, если и только если замкнуты ровно 4 из этих переключателей.

§8. Особые методы минимизации.

Выше мы рассматривали упрощение контактных схем тождественным преобразованием формул на основе законов алгебры логики. Как было видно из приведенных примеров, этот прием позволяет весьма эффективно решать вопросы о минимизации контактных схем. Однако при этом мы часто не бываем уверены в том, что выбранный путь преобразования формулы является наиболее экономным и что полученный результат обеспечивает построение минимальной контактной схемы. Поэтому на практике, помимо приведенного выше приема применяются другие методы минимизации: графический метод, построение матрицы Карно, метод неопределенных коэффициентов и др.

Остановимся кратко на этих методах.

Графический метод.

Формулу, в которую входит одна переменная, можно изобразить отрезком прямой, один конец которого будет соответствовать значению 0, другой – значению 1.

Ф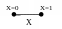 ормула с двумя переменными изображаются квадратом, вершины которого соответствуют членам совершенной дизъюнктивной нормальной формы.

В дальнейшем договоримся операцию  в членах СДНФ не писать, то есть XY будем записывать как XY.

На рисунке эти члены расположены так, что при переходе от одной вершины к любой соседней меняется только одна переменная.

При логическом сложении (дизъюнкции) двух членов, находящихся на концах какой-либо одной стороны квадрата, одна переменная будет исключаться. Так, при сложении XY и XY переменная Y будет исключена и вместо суммы двух членов останется одна переменная X:

XYXYX(YY) X.

Аналогично суммы любых двух других членов, расположенных на концах того или иного отрезка заменяются одной буквой:

XYXYY; XYXYX; XYXYY.

Это обстоятельство позволяет минимизировать формулы с двумя переменными, которые предварительно должны быть приведены к СДНФ.

1. Пусть нам дана такая СДНФ:

XYXYXY.

П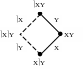 остроим квадрат, и вершины его, соответствующие членам СДНФ, отметим жирными точками. Сплошными линиями отметим отрезки, соединяющие их, а остальные стороны квадрата отметим пунктиром.

Имея в виду изложенное выше, мы можем по чертежу сразу написать минимальную форму:

XYXYXYXY.

2. Пусть дана СДНФ:



X

XYXYXYXY.

Все вершины квадрата отмечены жирными точками, стороны сплошными линиями.

Для замены этой формулы достаточно брать две любые противоположные стороны квадрата, т. к. ими охватываются все четыре вершины его. Получаем XX или YY. Любая сумма равна 1, следовательно формула тождественно истинна.

Формулы с тремя переменными удобно изображать кубом. Такое графическое выражение представляет собой весьма эффективное средство минимизации формул с тремя переменными.

Пусть дана следующая СДНФ:

XYZXYZXYZXYZ.

Н а рисунке изображен куб, соответствующий данной СДНФ.

Сумма любой пары членов, находящихся на смежных вершинах, заменяется двухчленной конъюнкцией, так как исключается одна переменная:

XYZXYZXY(ZZ)ZY;

XYZXYZXZ(YY)XZ;

XYZXYZYZ(XX)YZ.

Следовательно, ребра куба соответствуют двухчленным конъюнкциям. Как видно из чертежа, все слагаемые данной формулы (все вершины куба, отмеченные жирными точками) охватываются двумя ребрами: XY и YZ. Таким образом, XYZXYZXYZXYZXYYZ.

Данная формула реализуется минимальной контактной схемой, содержащей четыре контакта: