
- •§ 4. Формула Стокса
- •Глава VI. Элементы теории поля
- •§ 1. Скалярное поле. Градиент. Производная по направлению
- •1. Скалярное поле. Поверхности и линии уровня
- •2. Производная по направлению
- •3. Градиент скалярного поля. Его свойства. Связь градиента скалярного поля с производной по направлению. Оператор Гамильтона
- •§ 2. Векторное поле
- •1. Векторное поле. Векторные линии и векторные поверхности
2. Производная по направлению
Для
изучения свойств скалярного поля
прежде всего бывает необходимо выяснить,
как меняется это поле при переходе от
одной точки поля к другой. Допустим, что
мы рассматриваем скалярное поле
,
где функция
дифференцируема в каждой точке поля,
т.е. её полное приращение
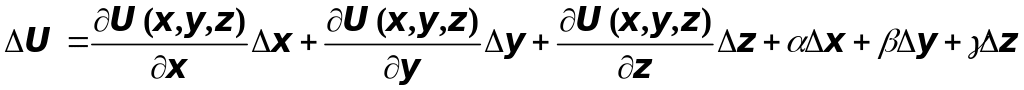 ,
,
где
![]() ,
,
![]() и
и
![]() стремятся к нулю, если
стремятся к нулю, если
![]() .
.
Выберем
в поле скалярной величины
некоторое направление, определяемое
осью
![]() (
(![]() - орт этого направления).
- орт этого направления).
Возьмём
на оси
две точки
и
![]() .
Обозначим пр
.
Обозначим пр![]() (рис. 1).
(рис. 1).
О чевидно,
что
чевидно,
что
![]() ,
если направление вектора
,
если направление вектора
![]() совпадает с направлением оси
и
совпадает с направлением оси
и
![]() ,
если они противоположны.
,
если они противоположны.
Дадим теперь определение производной функции по направлению .
Определение. Производной функции по направлению называется
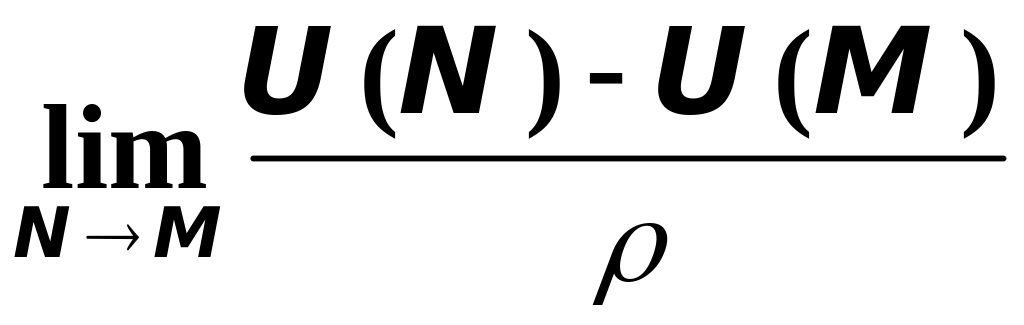 ,
,
где
![]() пр
пр![]() ,
а точки
,
а точки
![]() и
и
![]() лежат на оси
.
лежат на оси
.
Производная по направлению обозначается
![]() ,
т.е.
,
т.е.
 .
(рис. 1)
.
(рис. 1)
Примем теперь во внимание, что функция дифференцируема, тогда получим
![]() .
.
Если ось
образует углы
,
и
с координатными осями, то очевидно, что
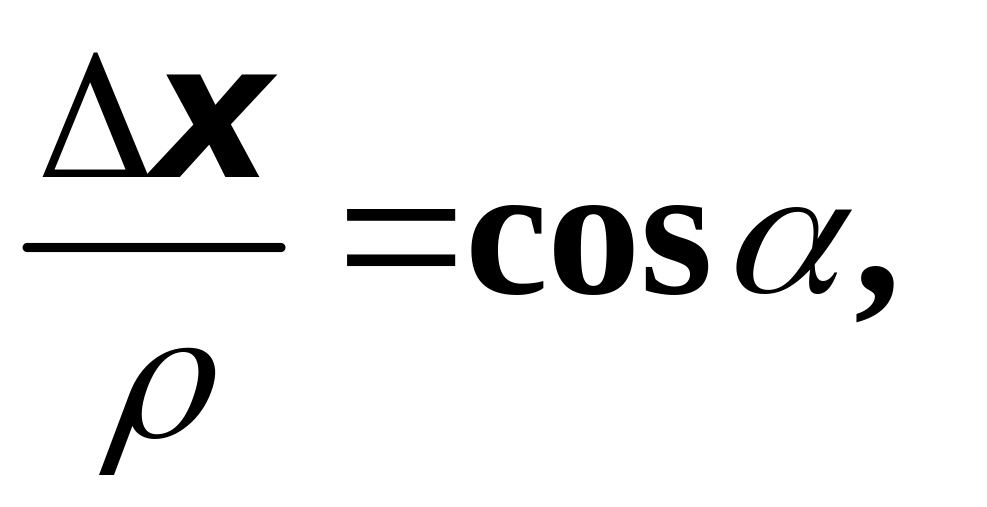
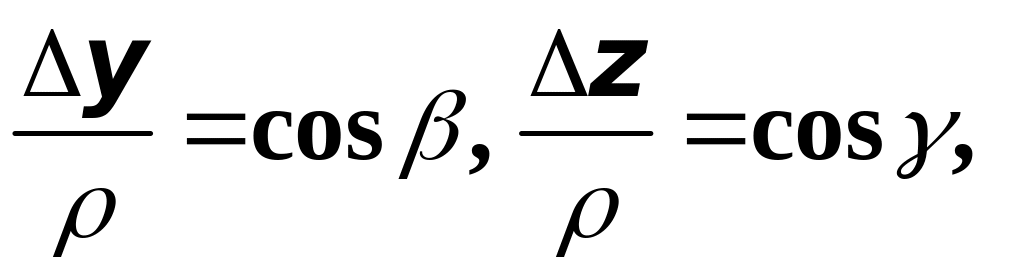 а тогда в пределе получим:
а тогда в пределе получим:
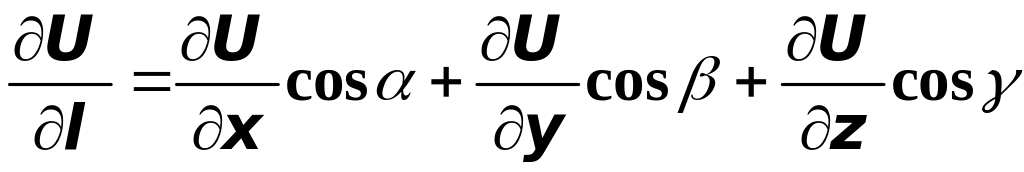 .
.
Ясно, что единичный вектор направления
имеет своими координатами направляющие
косинусы оси
,
т.е.
![]() ,
где
,
и
- углы, которые вектор
образует с координатными осями.
Следовательно, производную по направлению
можно представить в виде скалярного
произведения вектора
,
где
,
и
- углы, которые вектор
образует с координатными осями.
Следовательно, производную по направлению
можно представить в виде скалярного
произведения вектора
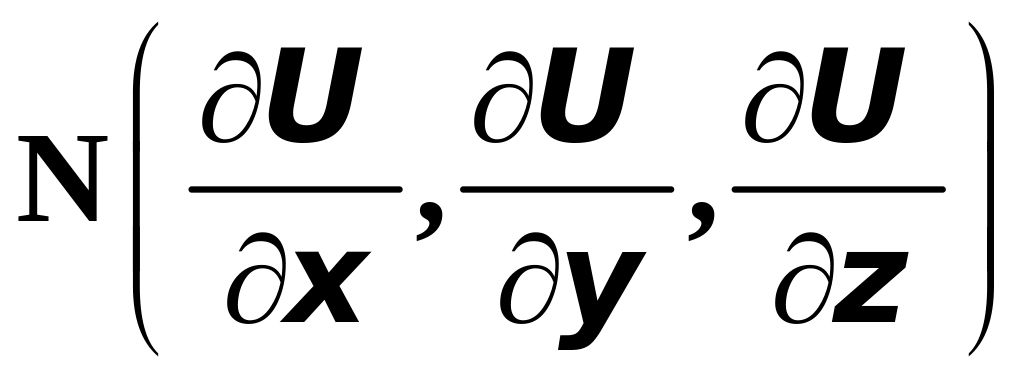 и вектора
,
т.е.
и вектора
,
т.е.
![]() ,
где вектор
,
где вектор
 (это было получено ранее) есть ни что
иное, как нормаль к поверхности уровня
.
Напомним, что производная имеет
механический смысл - скорость. Значит,
производная по направлению даёт нам
скорость изменения поля
в направлении оси
.
Нетрудно заметить также, что мы уже
ранее рассматривали производные по
направлению, а именно, это были производные
по направлению координатных осей
,
и
,
т.е. изученные ранее частные производные
(это было получено ранее) есть ни что
иное, как нормаль к поверхности уровня
.
Напомним, что производная имеет
механический смысл - скорость. Значит,
производная по направлению даёт нам
скорость изменения поля
в направлении оси
.
Нетрудно заметить также, что мы уже
ранее рассматривали производные по
направлению, а именно, это были производные
по направлению координатных осей
,
и
,
т.е. изученные ранее частные производные
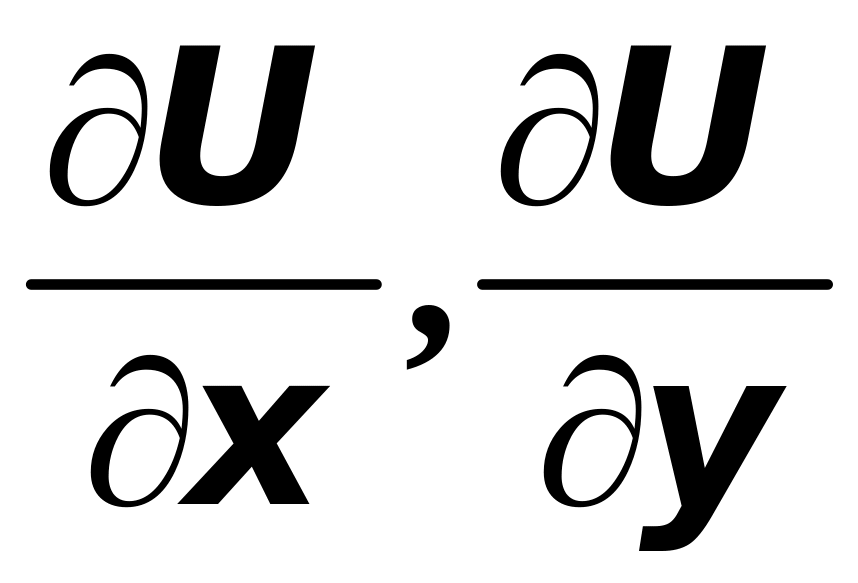 и
и
![]() .
.
Заметим, что понятие производной по направлению обобщают и на случай, когда это направление задаётся некоторой кривой линией . В этом случае в качестве направляющих косинусов направления берут направляющие косинусы касательной к кривой в точке дифференцирования.
Пример.
Найти производную скалярного поля
![]() по направлению кривой
по направлению кривой
![]() от точки
от точки
![]() к точке
к точке
![]() в точке
в точке
![]() .
.
Р ешение.
Найдём единичный вектор
ешение.
Найдём единичный вектор
![]() ,
касательный к параболе
в точке
.
Найдём угловой коэффициент прямой, на
которой лежит вектор
,
касательный к параболе
в точке
.
Найдём угловой коэффициент прямой, на
которой лежит вектор
![]() :
:
![]() .
.
Прямая имеет угловой коэффициент
![]() и проходит через точку
,
следовательно, её уравнение
и проходит через точку
,
следовательно, её уравнение
![]() .
.
Запишем это уравнение в каноническом
виде:
![]() .
Вектор
.
Вектор
![]() - направляющий вектор этой прямой, причём
его направление соответствует направление
на кривой от точки
к точке
.
Соответствующий ему единичный вектор
- направляющий вектор этой прямой, причём
его направление соответствует направление
на кривой от точки
к точке
.
Соответствующий ему единичный вектор
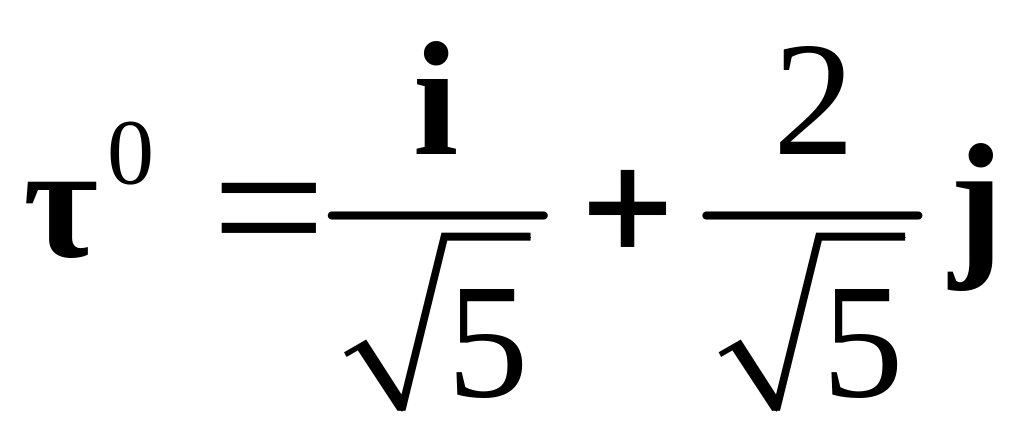 ,
т.е. его направляющие косинусы
,
т.е. его направляющие косинусы
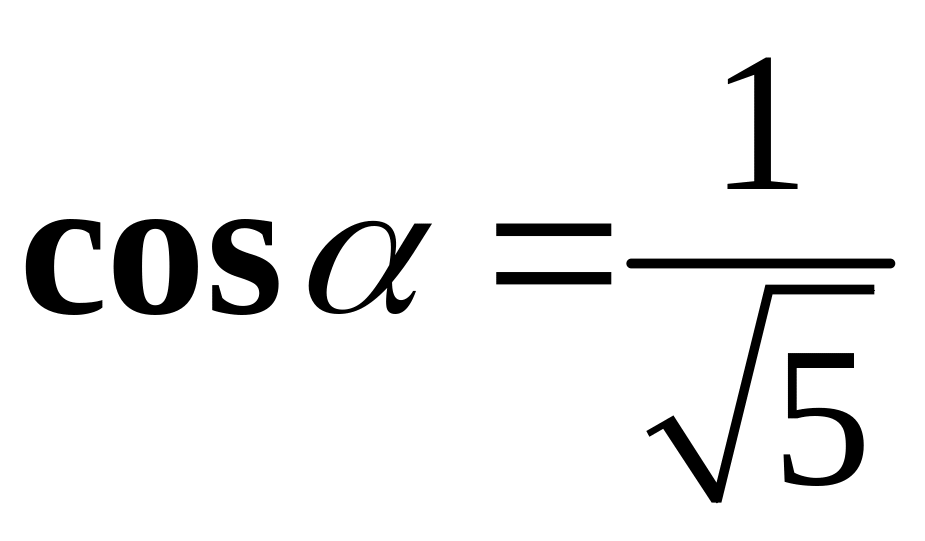 ,
,
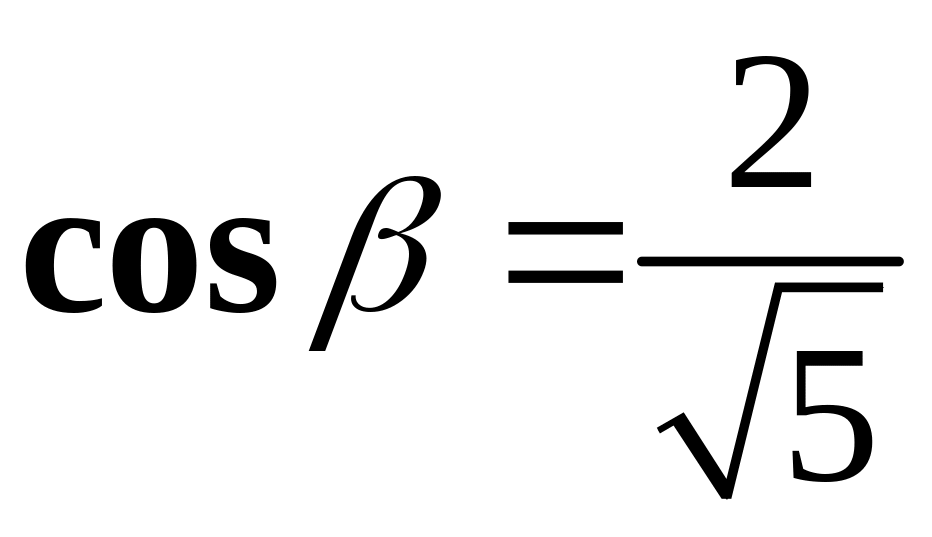 .
.
Найдём теперь
 ,
,
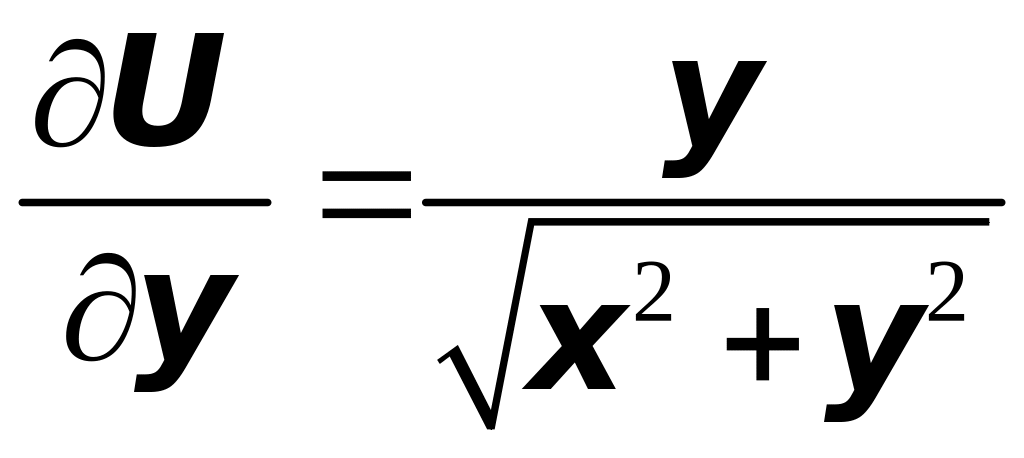 ,
а тогда производная по направлению
функции
в точке
по кривой
от точки
к точке
будет
,
а тогда производная по направлению
функции
в точке
по кривой
от точки
к точке
будет
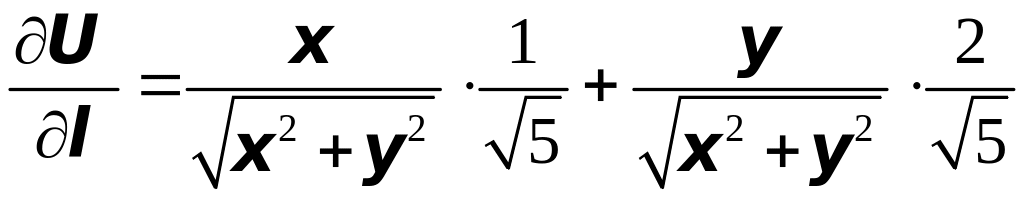 .
.
3. Градиент скалярного поля. Его свойства. Связь градиента скалярного поля с производной по направлению. Оператор Гамильтона
Рассмотрим скалярное поле и предположим, что в некоторой области функция дифференцируема, т.е. существуют непрерывные частные производные
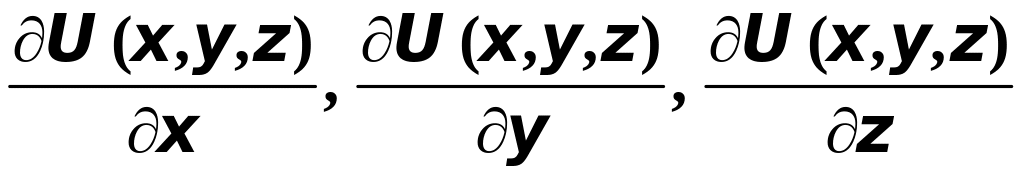 ,
,
а
поверхности уровня
не имеют особых точек, т.е. таких точек,
в которых все три частные производные
обращались бы в ноль. При сделанных
предположениях поверхность уровня
в каждой своей точке имеет касательную
плоскость, а следовательно и нормаль к
поверхности
![]() ,
которая, как известно, имеет координаты
,
которая, как известно, имеет координаты
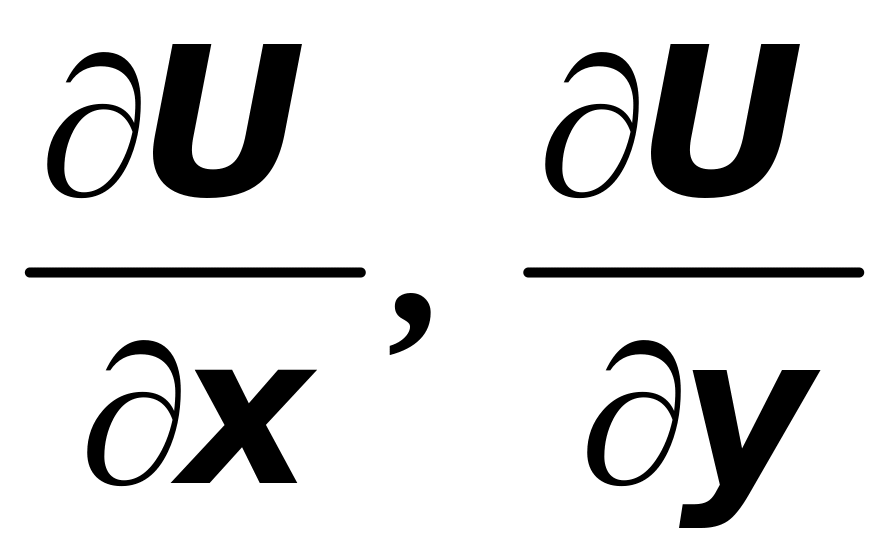 и
,
т.е.
и
,
т.е.
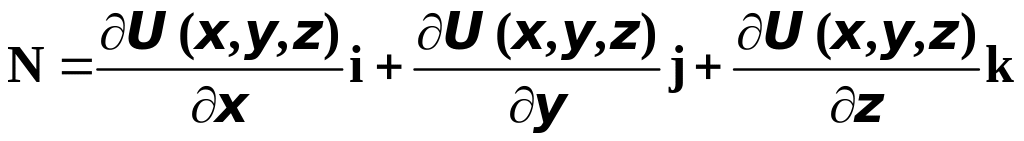 .
.
В правой части здесь стоит скалярное
произведение векторов
![]() и
,
т.е.
и
,
т.е.
![]() пр
пр![]() .
Скалярное произведение вектора на
некоторый орт можно осмыслить как
проекцию этого вектора на орт,
следовательно,
пр
.
Очевидно, что эта производная имеет
наибольшее значение, если направление
оси
совпадает с направлением градиента,
т.е. можно сделать вывод, что в направлении
градиента скалярное поле имеет наибольшую
скорость изменения. Вычислим эту
наибольшую скорость изменения скалярного
поля: т.к.
.
Скалярное произведение вектора на
некоторый орт можно осмыслить как
проекцию этого вектора на орт,
следовательно,
пр
.
Очевидно, что эта производная имеет
наибольшее значение, если направление
оси
совпадает с направлением градиента,
т.е. можно сделать вывод, что в направлении
градиента скалярное поле имеет наибольшую
скорость изменения. Вычислим эту
наибольшую скорость изменения скалярного
поля: т.к.
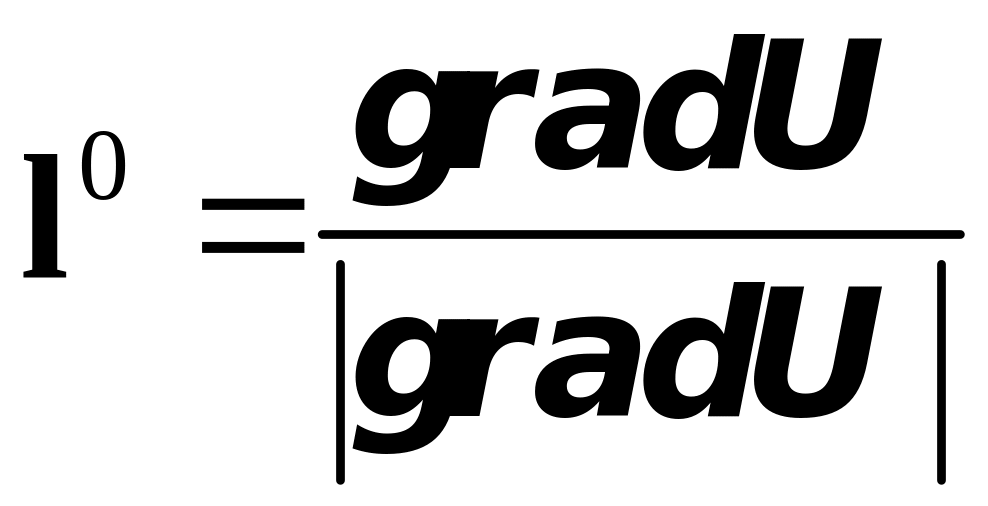 то ясно, что
то ясно, что

 .
.
Итак, можно сделать окончательный вывод: в направлении своего градиента скалярное поле имеет наибольшую скорость изменения, и эта скорость равна модулю градиента скалярного поля.
Задача
2. Дано поле температур
![]() .
.
Найти
наибольшую скорость изменения поля
![]() в точке
в точке
![]() .
.
Решение. Абсолютная величина наибольшей скорости изменения поля, совпадающая со значением модуля градиента поля температур, будет равна
![]() .
.
Очевидно также следующие свойства градиента скалярного поля:
1)
![]()
2)
![]()
3)
![]() .
.
В этом нетрудно убедиться самостоятельно.
Для компактной записи градиента
скалярного поля введём в рассмотрением
символический вектор - оператор Гамильтона
(вектор "набла"), который обозначается
так: "![]() "
и равен по определению
"
и равен по определению
 ,
,
т.е. ясно, что с помощью оператора Гамильтона градиент скалярного поля можно следующим образом:
![]() .
.
В заключение этого параграфа решим ещё одну задачу.
Задача 3. Найти градиент потенциала электростатического поля, образованного точечным зарядом
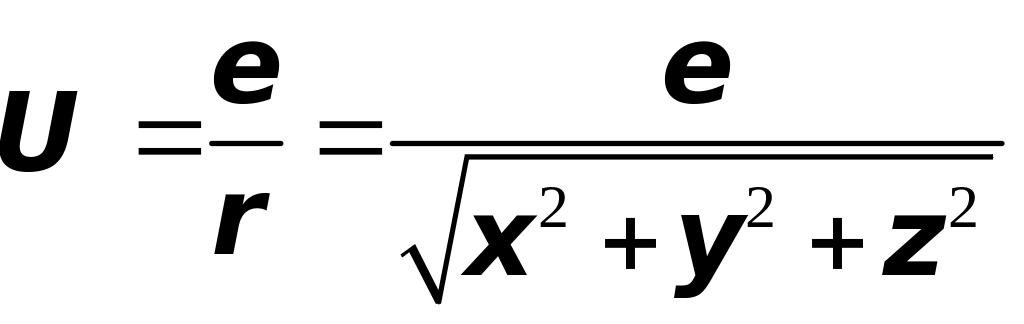 .
.
Решение.
Найдите прежде всего поверхности уровня
данного поля. Положим
![]() ,
т.е.
,
т.е.
 ,
т.е. поверхности уровня представляют
собою концентрические сферы с центром
в точке, где находится электрический
заряд.
,
т.е. поверхности уровня представляют
собою концентрические сферы с центром
в точке, где находится электрический
заряд.
Найдём
![]() ,
где
,
где
![]() ,
,
![]() ,
т.е. градиент направлен по радиусу
рассматриваемого семейства сфер, причём
функция
возрастает с уменьшением
,
т.е. градиент направлен по радиусу
рассматриваемого семейства сфер, причём
функция
возрастает с уменьшением
![]() ;
вектор
;
вектор
![]() .
.
называется напряженностью электрического поля.
