Ранговый дисперсионный анализ Краскала–Уоллиса

Любую шкалу измерения можно всегда понизить до более простой, причем выводы, справедливые в простейших шкалах, будут более общими и надежными, чем в высших шкалах. Поэтому кроме обычного дисперсион­ного анализа используют также ранговые дисперсионные анализы Фридмена или Краскала–Уоллиса. Так, в стандартном дисперсионном анализе требуется, чтобы данные в каждой группе были распределены нормально с одинаковой дисперсией. Если эти предпосылки не выполняются, выводы дисперсионного анализа становятся сомнительными. Наличие выбросов (далеко отклоняющихся значений) также способно исказить результаты анализа. После перехода к рангам, некоторая часть информации будет потеряна, однако снимаются все вышеперечисленные обременительные предположения.

Например, в следующей таблице приведены данные о времени появления реакции в 4-х группах, которые отличаются условиями проведения опыта. В последних строках таблицы вычислены средние и дисперсии в каждой группе, откуда видна нежелательная особенность – большим значениям средних групповых соответствуют большие значения дисперсии.

Время появления реакции в 4-х группах

№	І	ІІ	ІІІ	IV
1	0,5	1,1	0,9	0,4
2	0,7	1,6	2,1	1,9
3	1,0	3,7	3,0	2,4
4	1,2	4,3	4,7	2,8
5	1,7	4,7	6,4	3,9
6	2,3	5,1	6,6	5,4
7	2,4	6,6	8,5	11,4
8	3,1	8,8	10,0	20,4
Cередние	1,6	4,5	5,3	6,1
Дисперсии	0,741	5,494	8,809	39,077

Как правило, время появления какого-то события имеет экспоненциальное или гамма-распределение, которые существенно отличаются от нормального. Кроме того, последнее наблюдение в 4-й группе очень похоже на выброс (такие отклонения допустимы для экспоненциального закона, но нетипичны для нормального распределения).

По методу Краскала–Уоллиса необходимо все данные (n = 48 = 32) ранжировать и для каждой группы найти средние ранги v_i .

Доказано, что статистика

имеет асимптотическое ²–распределение с ЧСС = р – 1 , где р – число групп.

Если 0-гипотеза отклоняется, то для выявления значимых различий необходимо сделать парных сравнений по критерию Стьюдента

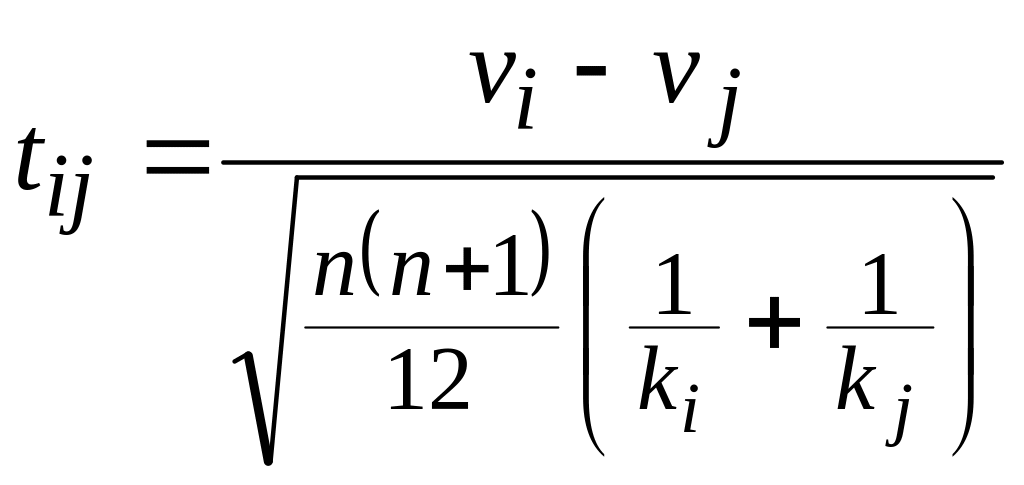
с числом степеней свободы с df_ij = k_i + k_j – 2.

Итак, ранжируем данные предыдущей таблицы и подсчитываем средние ранги в каждой группе:

Ранжированнае данные

№	І	ІІ	ІІІ	IV
1	2	6	4	1
2	3	8	11	10
3	5	18	16	13,5
4	7	20	21,5	15
5	9	21,5	25	19
6	12	24	26,5	23
7	13,5	26,5	28	31
8	17	29	30	32
Суммы	68,5	153	162	144,5
Средние	8,563	19,125	20,250	18,063

Расположенные в порядке возрастания наблюдения 13 и 14 оказались одинаковыми, поэтому присваиваем им одинаковый средний ранг 13,5; одинаковыми оказались также пары наблюдения 21 – 22 и 26 – 27, присваива­ем этим парам средние ранги 21,5 и 26;5.

В последней строке таблицы подсчитаны средние ранги по группам.

Вычисляем статистику Краскала–Уоллиса (p = 4, k_i = 8, n = 32):

Это значение сравниваем с табличным . Поскольку Н = 7,85 > H_0,05 , то нуль-гипотеза отклоняется с уровнем значи­мости 5% , т.е. считаем, что между группами имеются значимые различия (что означает оговорка "с уровнем значимости 5%"?).

Теперь необходимо выяснить, какие именно группы значимо отличаются от остальных. Вычисляем разность средних рангов для 1-й и 3-й групп (максимальная разница): ₁₃ = 20,250 – 8,563 = 11,687.

Статистика Стьюдента для этих групп

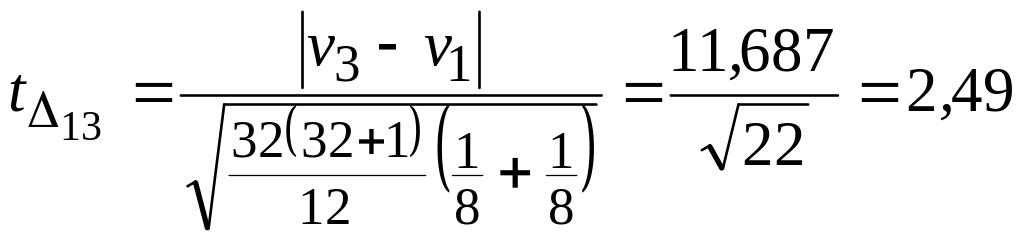
оказалась больше табличного значения t_0,05(8 + 8 – 2) = 2,14, т.е. можно считать, что между группами 1 – 3 есть значимые различия (с уровнем значимости 5%). Остальные разности не значимы.

Приведем некоторые соображения для вывода статистики Краскала–Уоллиса. Напоминаем, что если величины x_i распределены нормально x_i ~ N(a_i , _i), то сумма квадратов стандартизованных величин распределена по закону ² . Краскал и Уоллис рассматривали средние ранги v_i в каждой из p групп объема k_i . Нуль-гипотеза заключается в утверждении, что элементы в каждую группу отбираются случайным образом, поэтому ожидается (математическое ожидание), что все a_i  одинаковы и равны общему среднему рангу всех n наблюдений (ранги – последователь­ные номера от1 до n). Известны вероятности попадания элемента в ту или иную группы – они пропорциональны объемам выборок . Этого достаточно, чтобы вывести формулы для дисперсий средних рангов . Согласно центральной предельной теореме, средние ранги случайных выборок объема k_i > 5 распределены практически нормально. Составляем стандартную статистику Пирсона , где для больших n можно пренебречь сомножителями . Новая статистика будет иметь асимптотическое ² – распределение. Число степеней свободы здесь на единицу меньше числа групп, т.к. общая сумма рангов известна – это связь, наложенная на отклонения . В новой статистике Стьюдента для сравнения средних рангов двух групп (v_i – v_j) также пренебрегаем сомножителями :

.
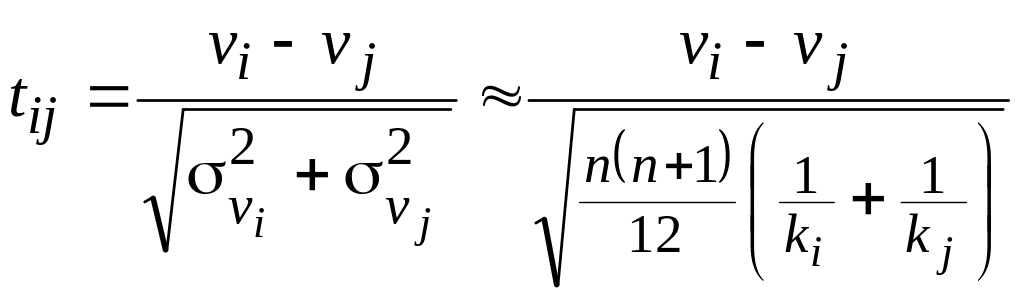