Свойства обратной функции
Теорема
4 ( о
монотонности и непрерывности)
Пусть
X
=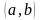 ,
тогда
,
тогда
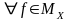
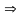
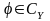 ,
где
,
где
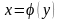 есть однозначная обратная функция на
множестве
есть однозначная обратная функция на
множестве
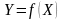 ,
т.е. всякая строго монотонная на интервале
функция имеет строго монотонную
непрерывную однозначную обратную.
,
т.е. всякая строго монотонная на интервале
функция имеет строго монотонную
непрерывную однозначную обратную.
Доказательство.
Покажем
методом от противного, что
( для случая строгого возрастания).
Предположим,
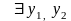
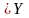 такие, что
такие, что
 <
<
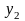 и
и
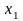 =
=
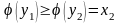 .
Отсюда имеем
>
.
Отсюда имеем
>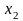 и
=
и
=
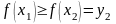 ,
т.к.
,
,
т.к.
,
 ,
,
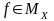 .
Полученное противоречие и доказывает
строгое возрастание обратной функции
на множестве Y.
.
Полученное противоречие и доказывает
строгое возрастание обратной функции
на множестве Y.
Аналогично
из строгого убывания функции
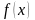 на
следует строго убывание ее обратной.
на
следует строго убывание ее обратной.
Докажем,
теперь по определению непрерывность
функции
на множестве
:
для
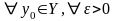
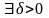 ,
такое, что
,
такое, что
 удовлетворяющего неравенству
удовлетворяющего неравенству
 будем иметь
будем иметь
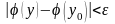 .
Пусть
.
Пусть
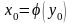 ,
а
,
а
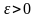 столь мало, что
столь мало, что
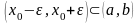 .
Тогда в силу строгого возрастания
функции
на
число
.
Тогда в силу строгого возрастания
функции
на
число
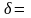 наим.
наим.
 удовлетворяет всем требованиям указанного
определения непрерывности.
удовлетворяет всем требованиям указанного
определения непрерывности.
Действительно,
пусть
 ,
,
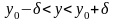 тогда
тогда
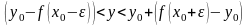 ,
т.е.
,
т.е.
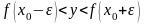 и т.к.
- возрастает строго, то
и т.к.
- возрастает строго, то
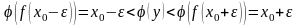 ,
т.е.
,
т.е.
 .
Значит, из того, что
.
Значит, из того, что
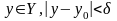 следует , что
.
следует , что
.
Теорема
доказана.
Замечание.
На
самом деле доказана теорема: если
- строго возрастает на множестве
и
множество значений ее – интервал
,
то
- непрерывна на
.
Это есть некоторый признак непрерывности
строго монотонной функции.


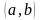 ,
тогда
,
тогда
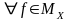
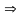
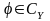 ,
где
,
где
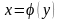 есть однозначная обратная функция на
множестве
есть однозначная обратная функция на
множестве
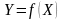 ,
т.е. всякая строго монотонная на интервале
функция имеет строго монотонную
непрерывную однозначную обратную.
,
т.е. всякая строго монотонная на интервале
функция имеет строго монотонную
непрерывную однозначную обратную.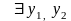
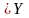 такие, что
такие, что
 <
<
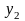 и
и
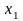 =
=
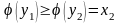 .
Отсюда имеем
>
.
Отсюда имеем
>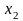 и
=
и
=
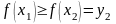 ,
т.к.
,
,
т.к.
,
 ,
,
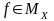 .
Полученное противоречие и доказывает
строгое возрастание обратной функции
на множестве Y.
.
Полученное противоречие и доказывает
строгое возрастание обратной функции
на множестве Y.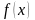 на
следует строго убывание ее обратной.
на
следует строго убывание ее обратной.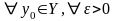
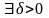 ,
такое, что
,
такое, что
 удовлетворяющего неравенству
удовлетворяющего неравенству
 будем иметь
будем иметь
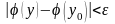 .
Пусть
.
Пусть
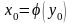 ,
а
,
а
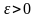 столь мало, что
столь мало, что
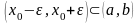 .
Тогда в силу строгого возрастания
функции
на
число
.
Тогда в силу строгого возрастания
функции
на
число
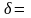 наим.
наим.
 удовлетворяет всем требованиям указанного
определения непрерывности.
удовлетворяет всем требованиям указанного
определения непрерывности. ,
,
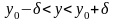 тогда
тогда
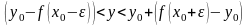 ,
т.е.
,
т.е.
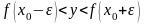 и т.к.
- возрастает строго, то
и т.к.
- возрастает строго, то
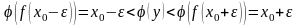 ,
т.е.
,
т.е.
 .
Значит, из того, что
.
Значит, из того, что
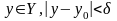 следует , что
.
следует , что
.