
Федеральное агентство по образованию
ГОУ ВПО
Челябинский государственный педагогический университет
Математический факультет
Кафедра математического анализа
Квалификационная работа
«Определение и изучение элементарных функций средствами математического анализа»
Выполнила: студентка 512 группы
математического факультета
Филюнина А.В.
Научный руководитель: доцент, кандидат
физико-математических наук
Гейт Н.Ж.
Челябинск 2012
Содержание
Введение…………………………………………………………………………………………………………..3
Основные сведения………………………………………………………………………………………….5
Глава 1. Обратная функция………………………………………………………………………………12
1.1. Понятие обратной функции………………………………………………………………………12
1.2. Условия существования обратной функции……………………………………………..13
1.3. Свойства обратной функции……………………………………………………………………..16
Глава 2. Определение и изучение элементарных функций средствами математического анализа
2.1. Степенная функция с целым неотрицательным показателем
2.2. Степенная функция с целым отрицательным показателем
2.3. Степень с рациональным показателем
2.4. Показательная функция
2.5. Логарифмическая функция
2.6. Обратные тригонометрические функции
Заключение
Литература
Введение
Целью данной квалификационной работы является изучение элементарных функций средствами математического анализа. Введение и изучение свойств показательной, логарифмической, тригонометрических функций отлично от традиционного, излагаемого в основных учебниках по анализу.
Математический анализ (МА)– учение о функциях, её свойствах и применениях. Основы МА создавались многими учёными в течение всего 17 века, но основоположниками являются английский учёный Исаак Ньютон и немецкий учёный Готфрид Лейбниц. Однако знание МА достраивали в 18 веке, а особенно в 19 веке, когда французский математик Огюст Коши создал теорию пределов, определил теорию через предел и построил приложение дифференциального исчисления. К настоящему времени МА сильно разросся и сейчас является главной ведущей частью математики.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
алгебраические:
степенная;
рациональная
трансцендентные:
показательная и логарифмическая;
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
В первой главе подробно излагаются обратные функции: дается понятие обратной функции, рассматриваются условия существования обратной функции, описываются свойства обратной функции по свойствам прямой.
Во второй главе в качестве простейшей функции, используемой для построения всех остальных, выбирается степенная функция с целым неотрицательным показателем.
После введения и изучения свойств степенной функции с целым отрицательным и рациональным показателями, с помощью предельного перехода вводится показательная функция. Затем изучаются средствами анализа свойства этой функции, дифференцируемость и строгое возрастание функции на всей области определения.
После этого вводится логарифмическая функция, как обратная показательной, и изучаются её свойства.
Далее вводятся и изучаются тригонометрические функции и обратные тригонометрическим функциям.
Основные сведения
Определение 1.
Пусть даны две переменные х и у с областями изменения Х и У. Предположим, что по условиям вопроса переменной х может быть приписано произвольное значение из области Х без каких-либо ограничений. Тогда переменная у называется функцией от переменной х в области ее изменения Х, если по некоторому правилу или закону каждого значению х из Х ставится в соответствие одно определенное значение у.
Независимая переменная х называется аргументом функции.
Область Х изменения аргумента называют областью определения функции, а область У – областью значения функции.
Область определения функции — множество, на котором задаётся функция.
Область значений функции — множество значений, которые принимает функция в результате ее применения.
Для указания того факта, что у есть функция от х, пишут: у=f(х).
Определение 2.
Ф ункцию
называют монотонно возрастающей (
рис.1а), если с увеличением аргумента
значение функции увеличивается и
монотонно убывающей (рис. 1б), если с
увеличением аргумента значение функции
уменьшается.
ункцию
называют монотонно возрастающей (
рис.1а), если с увеличением аргумента
значение функции увеличивается и
монотонно убывающей (рис. 1б), если с
увеличением аргумента значение функции
уменьшается.
Более строгое определение монотонности.
Функция
у = f(х)
называется монотонно
возрастающей
на интервале (a,b),
если для любых х1
и х2
, принадлежащих
этому интервалу, из неравенства х2
 х1
следует неравенство f(х2)
f(х1).
Функция у = f(х)
называется монотонно
убывающей
на интервале (a,b),
если для любых х1
и х2
, принадлежащих
этому интервалу, из неравенства х2
х1
следует неравенство f(х2)
х1
следует неравенство f(х2)
f(х1).
Функция у = f(х)
называется монотонно
убывающей
на интервале (a,b),
если для любых х1
и х2
, принадлежащих
этому интервалу, из неравенства х2
х1
следует неравенство f(х2) f(х1).
Естественно, что интервал (a,b)
взят из области определения функции.
f(х1).
Естественно, что интервал (a,b)
взят из области определения функции.
Определение 3.
Функция
f(х)
имеет пределом число А при стремлении
х к а, если для каждого числа ε
0
найдется такое число δ
0,
что |f(х)
- А|
ε
лишь только |х-а| (х
(х а),
х
а),
х Х.
А=lim
f(х)
при х стремящемся к а.
Х.
А=lim
f(х)
при х стремящемся к а.
В самой точке х=а функция может и не существовать. Такова, например функция у= в точке х=0.
= 1, хотя в точке х=0 значение функции не определено.
В определении предела функции не указывается, каким образом аргумент х стремится к числу а. Если предел функции в точке а существует, то он не зависит от способа приближения аргумента х к точке а. Пусть переменная величина х обозначает движущуюся точку на оси абсцисс. Тогда стремление этой точки к а может происходить справа или слева. Результат стремления точки справа к а будем обозначать через а+0, а слева через а-0.
Более строгое определение предела.
Число
В называется правым
пределом
функции при стремлении х к а справа
(т.е. по значениям х
а),
если для любого ε
0
найдется такое δ, что для всех х,
удовлетворяющих неравенству 0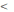 х
- а
х
- а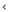 δ,
выполняется неравенство |f(х)
- В|
δ,
выполняется неравенство |f(х)
- В|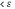 .
=f(а
+ 0)=В.
.
=f(а
+ 0)=В.
Число
С называется левым
пределом
f(х)
при стремлении х к точке а слева (т.е. по
значениям х), если для любого ε найдется
такое δ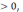 что
для всех х, удовлетворяющих неравенству
-δ
что
для всех х, удовлетворяющих неравенству
-δ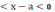 ,
выполняется неравенство |f(х)
- С|
.
,
выполняется неравенство |f(х)
- С|
.
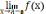 =f(а-0)=С.
=f(а-0)=С.
Из определения предела функции вытекает следующее утверждение:
Если предел функции в точке а существует, то существуют и равны между собой левый и правый пределы функций в этой точке (обратное верно).
Говорят,
что =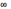 ,
если для любого числа D
найдется такое число
,
если для любого числа D
найдется такое число 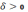 ,
что для всех х, удовлетворяющих неравенству
0, выполняется неравенство |f(х)|
,
что для всех х, удовлетворяющих неравенству
0, выполняется неравенство |f(х)|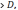 а функцию f(х)
при х в этом случае называют бесконечно
большой.
а функцию f(х)
при х в этом случае называют бесконечно
большой.
Вместо записи = употребляется и такая: f(х)→ при х .
Определение 4.
Функция F(х) называется бесконечно малой при х, стремящемся к а, если =0.
Функция
F(х)
называется бесконечно малой на
бесконечности, если 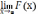 =0.
=0.
Согласно определению, значения функции F(х) по абсолютной величине становятся и продолжают оставаться меньше любого наперед заданного положительного числа, как только значения аргумента по абсолютной величине становятся достаточно большими.
Определение 5.
Пусть
z
= f(х,у)
определена на Х, называется непрерывной
в точке (х0,
у0)
Х,
если выполняются следующее условие:
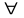 ε
ε
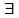 δ=δ(
δ=δ(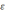 ),
такое что
),
такое что
 (х,у)
Sδ((х0,у0))
Х
(х,у)
Sδ((х0,у0))
Х 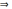 f(х,у)
Sδ(f(х0,у0)),
т.е. все значения функции сколь угодно
мало отличаются друг от друга, когда
значение аргумента близки к точке
(х0,у0).
f(х,у)
Sδ(f(х0,у0)),
т.е. все значения функции сколь угодно
мало отличаются друг от друга, когда
значение аргумента близки к точке
(х0,у0).
Определение 6.
Функция у=f(х) называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки (включая саму точку) и предел функции в точке существует и равен значению функции в самой этой точке, т.е. = A = f(х0)=f()
Из
определения следует, что  =
=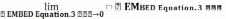 = 0.
= 0.
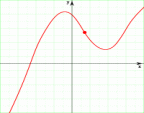
Определение 7.
Функция у = f(х) называется непрерывной на интервале, если она определена на этом интервале и непрерывна в каждой точке интервала.
Говорят, что точка х0 есть точка разрыва для функции у = f(х), если функция определена в окрестности этой точки ( в самой точке х0 функция может существовать, а может и не существовать), но в точке не выполняются условия непрерывности.

Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
ПРИМЕР.
Найти
точки разрыва функции f(х)=arctg
 ,
если они существуют.
,
если они существуют.
Решение.
Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке.
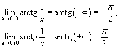
Видно,
что в точке x
= 0 существует
разрыв первого рода.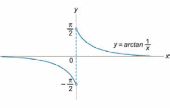
Определение 8.
Пусть
функция у=f(х)
определена в Х. Исходя из некоторого
значения х=х0
независимой переменной, придадим ему
приращение
 ,
не выводящее его из промежутка Х, так
что и новое значение х0+
,
не выводящее его из промежутка Х, так
что и новое значение х0+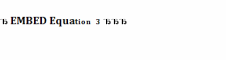 принадлежит этому промежутку. Тогда
значение функции у0
= f(х0)
получит приращение:
принадлежит этому промежутку. Тогда
значение функции у0
= f(х0)
получит приращение:
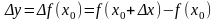
Если
существует предел отношения приращения
функции
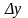 к
вызвавшему его приращению независимой
переменной
к
нулю, т.е.
к
вызвавшему его приращению независимой
переменной
к
нулю, т.е.
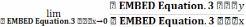 =
= 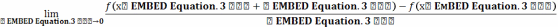 ,
то он называется производной
функции у =
f(х)
по независимой переменной х при данном
её значении (или в данной точке) х=х0.
,
то он называется производной
функции у =
f(х)
по независимой переменной х при данном
её значении (или в данной точке) х=х0.
Таким образом, производная при данном значении х=х0 - если существует – есть определенное число, если же производная существует по всем промежутке Х, т.е. при каждом значении х в этом промежутке, то она является функцией от х.
Определение 9.
Пусть имеем функцию у = f(х), определенную в некотором промежутке Х и непрерывную в рассматриваемой точке х0.
Тогда
приращению
аргумента
отвечает приращение
бесконечно малое вместе с
.
Важным вопросом является, существует
ли для
такая линейная относительно
бесконечно малая А (А=соnst),что
их разность оказывается, по сравнению
с
,
бесконечно малой высшего порядка:
(А=соnst),что
их разность оказывается, по сравнению
с
,
бесконечно малой высшего порядка:
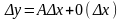 (*)
(*)
При
А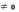 равенство (*)
показывает,
что бесконечно малая А
эквивалентна бесконечно малой
.
равенство (*)
показывает,
что бесконечно малая А
эквивалентна бесконечно малой
.
Если равенство (*) выполняется, то функция у = f(х) называется дифференцируемой (при данном значении х = х0), само же выражение А называется дифференциалом функции и обозначается: dy или df(х0).
Утверждение.
Для
того, чтобы функция у = f(х)
в точке х0
была дифференцируема, необходимо и
достаточно, чтобы для нее в этой точке
существовала конечная производная  =
= 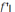 (х0).
(х0).
При выполнении этого условия равенство (*) имеет место при значении постоянной А, равном именно этой производной:
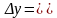
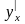 + 0(
).
+ 0(
).
