
Глава 1. Обратная функция
Понятие обратной функции
Определение 10.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X : x1. В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈X такой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X , которую и называют обратной функцией к функции y=f(x) и обозначают:
x=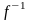 (y).
При этом очевидно, что функция f является
обратной к
функции f
(y).
При этом очевидно, что функция f является
обратной к
функции f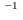 .
Поэтому
функции y=f(x) и x=
f
(y) называют
взаимно обратными.
.
Поэтому
функции y=f(x) и x=
f
(y) называют
взаимно обратными.
Т.о., если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f :Y→X и если y=f(x) то x= f (y), и если x= f (y), то y=f(x) и f (f(x))=x при любом x∈Х.
ПРИМЕР.
Если
f-
ограничение функции sin
на отрезок [- ],
],
то
отображение f:
[-
]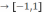 --
биекция.
--
биекция.
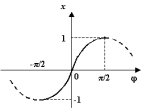
Поэтому
существует обратная функция 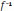 ,
называемая арксинусом и
обозначаемая
,
называемая арксинусом и
обозначаемая 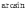 или
или  .
Таким образом,
.
Таким образом,

 sin
sin
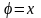 и
и
 [-
].
[-
].
Определение 11.
Пусть
функция у = f(х)
определена на множестве Х, У = f(х)
– множество её значений. Пусть для
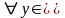 У
полный прообраз
У
полный прообраз 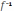 (y)
– одноэлементное множество. Тогда
У
соответствует единственное х
(y)
– одноэлементное множество. Тогда
У
соответствует единственное х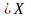 такое,
что у = f(х).
Таким образом, на множестве У задается
функция х =
такое,
что у = f(х).
Таким образом, на множестве У задается
функция х =
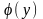 с
множеством значений Х =
с
множеством значений Х =
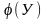 ,
называемая однозначной обратной
функцией.
,
называемая однозначной обратной
функцией.
Согласно
определения функция у = f(х)
производит отображение множества Х на
множество У, а обратная функция х =
-
У на Х: причём, для
У
имеем у = f(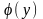 ),
),
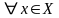 имеем х =
имеем х =
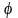 (f(х)).
Кроме того, для
х1,
х2
,
таких, что х1
х2
имеем f(х1)
(f(х)).
Кроме того, для
х1,
х2
,
таких, что х1
х2
имеем f(х1)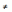 f(х2).
f(х2).
Обозначим
класс функций у = f(х),
х
и
У = f(Х),
для которых на множестве У существует
однозначная обратная функция х =
через
 (f
).
(f
).
Условия существования обратной функции
Теорема 1 (достаточное условие существования)
Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существует обратная функция x= (y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей). Доказательство.
По условию функция f строго возрастает на множестве X. Это значит для любых x1,x2∈X и x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f-1:Y→X . Покажем, что функция f-1 строго возрастает на множестве Y. Пусть y1 и y2 - любые точки из Y и y1<y2. Докажем, что x1=f-1(y1)<x2=f-1(y2). Допустим, чтоx1≥x2 . По условию функция f строго возрастает на X, поэтому из условия x1≥x2 вытекает неравенство y1=f(x1)≥y2=f(x2) , что противоречит условию y1<y2. Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
Теорема 2 (необходимое условие существования)
Пусть
Х = [a,b],
тогда (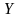 Сх
Сх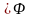 х)⟹
f
Mх
,
т.е. непрерывная на сегменте функция
при условии существования у нее
однозначной обратной функции должна
быть строго монотонной на этом сегменте.
х)⟹
f
Mх
,
т.е. непрерывная на сегменте функция
при условии существования у нее
однозначной обратной функции должна
быть строго монотонной на этом сегменте.
Доказательство.
1
)Докажем,
что из условия f
C[a,b]
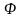 [
a,b]
следует,
что функция у = f(х),
х
[a,b],
принимает наибольшее и наименьшее
значения на концах [a,b].
Предположим противное. Пусть, например
f(х0)-
наименьшее значение, где а 0
[
a,b]
следует,
что функция у = f(х),
х
[a,b],
принимает наибольшее и наименьшее
значения на концах [a,b].
Предположим противное. Пусть, например
f(х0)-
наименьшее значение, где а 0
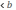 ,
f(х0)
,
f(х0)
 Тогда найдется точки
Тогда найдется точки
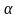 и
и
 такие, что а
такие, что а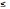 х0
b,
причём так как f
[
a,b]
,
то f(
)
f(
)
и f(
)
f(
).
х0
b,
причём так как f
[
a,b]
,
то f(
)
f(
)
и f(
)
f(
).
Пусть f(х0). Рассмотрим f(х) на [х0, ].
f(х0)⟹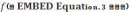 - одно из промежуточных значений функции,
т.е.
- одно из промежуточных значений функции,
т.е.
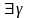 [х0,
] такое, что f(
[х0,
] такое, что f(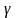 )
= f(
).
)
= f(
).
Но
 ,
т.к. а
х0.
Получаем противоречие с тем, что f(х)
имеет однозначную обратную функцию.
,
т.к. а
х0.
Получаем противоречие с тем, что f(х)
имеет однозначную обратную функцию.
2) Докажем теперь, что f M [a,b] . Пусть, например, inf f(х) = f(а) , sup f(х) = f(b), где х [a,b] установим строгое возрастание на [a,b] функции у = f(х). Пусть
х1, х2 [a,b], х12 такие, что f(х1) f(х2), f(х1) f(х2) т.к. f (a,b]. Тогда функция у = f(х) на сегменте [х1,b] достигает наименьшего значения во внутренней точке. Чего не может быть согласно рассуждений первого этапа доказательства.
Теорема доказана.
Теорема 3
Если
функция y=f(x) строго
возрастает (убывает) и непрерывна на
промежутке
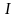 ,
то существует обратная
функция x=f-1(y),
которая определена на промежутке Ef=f(
) и
является на Е, строго возрастающей
(убывающей) и непрерывной.
,
то существует обратная
функция x=f-1(y),
которая определена на промежутке Ef=f(
) и
является на Е, строго возрастающей
(убывающей) и непрерывной.
Доказательство.
Для определенности предположим, что функция f строго возрастает на промежутке . По следствию из 2-ой теоремы Больцано-Коши область значений Ef=f( ) непрерывной функции f тоже есть промежуток. В силу строгого возрастания функции f для каждого y∈E существует единственная точка x∈ такая, что f(x)=y. Следовательно для функции f существует обратная функция f-1 определенная на промежутке Е и с множеством значений .
Покажем, что f -1строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1 и x2.
f-1(y1)=x1, и f-1(y2)=x2.
Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f -1(y1)<f -1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f-1 - строго возрастает на множестве Е.
Что и требовалось доказать.
