10. Предел функции. Связь между пределами функции на множестве и на его частях.
Определение 2.
= p
Число называется пределом функции f(x) при на множестве Е, если :
Пользуясь определением 2 можно дать определение предела через неравенства для конкретных .
, если
Например для p = , :
, если
Связь между пределами функции на множестве и его частях
Пусть
Тогда существование предела и равенству этих трех пределов.
11. Ограниченная функция. Ограниченность функции при .
1)
называется ограниченной сверху ( снизу,
просто ограниченной ), если множество
ее значений ограничено сверху ( снизу
, просто ограничено ).
2) Функция
f(x) называется
ограниченной сверху ( снизу, вообще на
Е ) при
,
если
в которой функция ограничена сверху (
снизу, на части
)
Ограниченность
функции при
Если
то функция ограничена при
Доказательство:
P
=
12. Предел последовательности. Ограниченность сходящейся последовательности.
1) Число p
называется пределом последовательности
Xn при
,
если
2) p
называется пределом последовательности
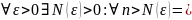
Последовательность является сходящейся, если она имеет конечный предел.
Всякая сходящаяся последовательность ограничена.
Пусть Xn – сходящаяся последовательность.
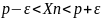
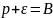
При n>N : A < Xn < B
a: min {x1, x2 … A }
b: max {x1,x2 .. Xn, B}
– последовательность является
ограниченной по определению.
13. Связь между пределом функции и пределом последовательности. Доказательство отсутствия предела.
Теорема. Связь между пределом функции и пределом последовательности.
Для того,
чтобы существовал предел функции при
равный p необходимо и
достаточно, чтобы для любой последовательности
при любом выборе
Для доказательства отсутствия пределов часто применяются следствия к пределу сложной функции.
1 следствие.
Если существует предел
,
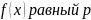то для
такого, что
,
и
= p, тогда
= p
2 следствие.
Если
,
то для любой последовательности
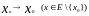при любом выборе
.
Пример:
Допустим,
докажем, что предел
не существует.
Возьмем
= 0
А теперь
возьмем
= 1
Для различных
последовательностей при
получаем разные
=> общего предела не существует.
14. Бесконечно-малые функции и их свойства.
Функция
называется бесконечно малой при
,
Е , если
Таким образом,
f(x) –
бесконечно малая функция при
Теорема. Критерий существования конечного предела функции, связанный с бесконечно малыми функциями.
Для того, чтобы существовал конечный предел функции при необходимо и достаточно, чтобы f(x) была представлена в виде f(x) = p + a(x)
a(x) – бесконечно малая функция при , Е
Свойства бесконечно малых функций.
1) Сумма конечного числа б.м.ф при , Е снова есть б.м.ф при , Е.
Доказательство:
f(x), g(x) – бесконечно малые функции при
f(x)
б.м.ф
g(x)
б.м.ф
2) Произведением б.м.ф на ограниченную функцию является бесконечно малая функция.
Следствие – произведение конечного числа б.м.ф есть б.м.ф
15. Критерий существования конечного предела функции на языке б.М.Ф. Бесконечно большие функции и их свойства.
Теорема. Критерий существования конечного предела функции, связанный с бесконечно малыми функциями.
Для того, чтобы существовал конечный предел функции при необходимо и достаточно, чтобы f(x) была представлена в виде f(x) = p + a(x)
a(x) – бесконечно малая функция при , Е
Бесконечно большие функции.
Функция
называется бесконечно большой при
,
Е , если
Свойства:
1) Произведение б.б.ф при на ограниченную есть б.б.ф
2) Связь между б.б.ф и б.м.ф
Если f(x)
при
– бесконечно большая функция, то ф-я
– бесконечно малая функция.