§22. Оператор Гамильтона

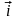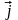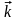Рассмотрим прямоугольную систему координат , и вместо векторов , , будем использовать векторы , , .

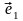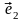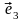Введём оператор (обозначим его символом “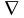 ”(набла)):

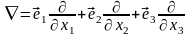
Он обладает как векторными, так и дифференциальными свойствами.

оператор (оператор Гамильтона) как дифференциальный оператор, действует на поля, которые стоят справа от него, и не действует на те, которые стоят слева:

.

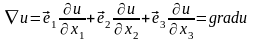Если векторное поле можно представить в виде 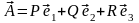, то получим:

.

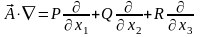Далее для удобства векторные поля будем представлять в виде . Тогда имеем:

,

,

.

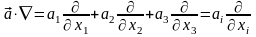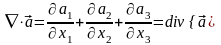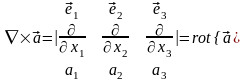Соответственно получаем:

,

,

,

.

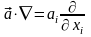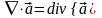Введём обозначение 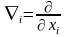. Тогда получаем:

, .

.

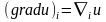§23. Потенциальные поля.

Векторное поле называется потенциальным, если существует скалярное поле ,

такое что 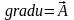. Скалярное поле называется потенциалом поля .

Теорема 1: Для того, что бы векторное поле было потенциальным, необходимо и достаточно, что бы .

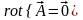Доказательство.

а) необходимость.

Дано: Существует скалярное поле , такое что . Требуется доказать, что . Из условия теоремы имеем:

.

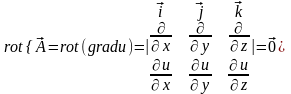Следовательно, поле градиента не вихревое.

б) достаточность.

Дано: . Требуется доказать, что существует скалярное поле , такое что .

Из теоремы о независимости криволинейного интеграла от пути интегрирования (*) следует, что если 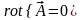, где (выполнено условие 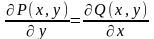из (*)), то существует функция такая, что (выражение является полным дифференциалом – условие (3) теоремы (*)). Следовательно:

.

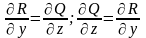Тогда получаем, что 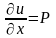, , 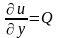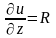. Следовательно:

,

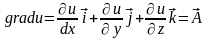что и требовалось доказать.

§24. Соленоидальные поля

В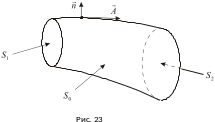 екторное поле называется соленоидальным, если 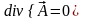, то есть в поле нет ни источников, ни стоков.

Если векторное поле - соленоидальное, то оно сохраняет интенсивность векторной трубки. Гидромеханический смысл этого утверждения: через любое ортогональное сечение векторной трубки за единицу времени протекает одинаковое количество несжимаемой жидкости.

Возьмём поверхность . Тогда поток векторного поля через поверхность равен:

.

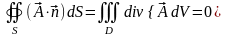Из условия, что 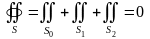и так как на поверхности следует, что , то есть протекает равное количество жидкости через площадки и .

Теорема 2: Для того, чтобы векторное поле было соленоидальным, необходимо и достаточно, чтобы существовало векторное поле 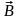, такое что 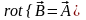(без доказательства).

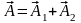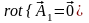Векторное поле , такое что называется векторным потенциалом векторного поля . Всякое векторное поле можно разложить на два компонента ( ), так что и .

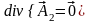§25.Ортогональные криволинейные системы координат. Координатные линии и поверхности. Параметры Ламе.

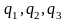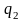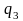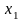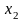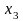Будем говорить, что в трёхмерном пространстве задана некоторая система координат, если между точками пространства и упорядоченными тройками чисел ( ) (где эти числа изменяются в определенных пределах) установлено взаимно однозначное соответствие. Предположим, что в этом пространстве задана прямоугольная система координат и известна связь между координатами , , и , , , то есть:

,

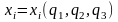где .

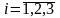Если мы зафиксируем координаты и , и будем менять координату в допустимых для неё пределах, то мы получим координатную линию . Её радиус вектор имеет следующий вид:

,

где , , - орты прямоугольной системы координат. Точно так же определяются координатные линии и .

Через каждую точку трехмерного пространства проходит три координатные линии. Если в каждой точке некоторой системы координат координатные линии взаимно перпендикулярны, то такая система называется ортогональной. Далее будем рассматривать только ортогональные системы координат.

Если зафиксировать координату , а позволить изменяться и , то получим координатную поверхность , заполненную координатными линиями и . Такую координатную поверхность обозначим либо ( , ). Аналогично можно определить координатные поверхности , .

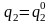У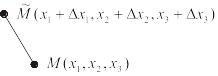 становим связь между изменением координат и длинной отрезка. Для малых отрезков:

либо .

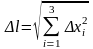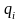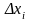Возьмём некоторую координатную линию . Тогда изменение координаты выразим через изменение координаты :

.

Если приращение 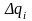- малое, то равно линейной части приращения. Тогда:

.

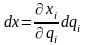Получим, что дифференциал дуги координатной линии будет иметь вид:

. (1)

Обозначим 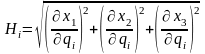. Этот коэффициент называется коэффициентом Ламе (Ламэ, Ляме).

П одставляя в (1) коэффициент Ламе, получим:

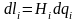, (2)

Из этой формулы следует, что 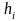имеет смысл коэффициента пропорциональности между малым изменением координаты и длины дуги координатной линии.

Обозначим бесконечно малый прямоугольник на координатной поверхности ( ), вырезанный координатными линиями (см. рис. 24). Его площадь обозначим 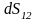. Тогда, используя формулу (2), получаем:

. .

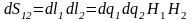А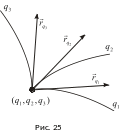 налогично можно получить формулу для двух произвольных координатных линий, то есть в общем случае:

,

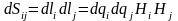где .

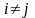Рассмотрим бесконечно малый параллелепипед, вырезанный координатными плоскостями. Подобно рассуждениям в рассмотренном выше случае, объём 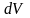этого параллелепипеда равен:

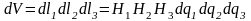. (3)

Обозначим радиус-вектор одной из вершин параллелепипеда:

.

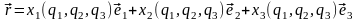Пусть векторы , , 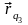- касательные к координатным линиям , , соответственно. Тогда - сторона параллелепипеда (см. рис. 25), и из (3) получаем:

.

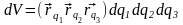В данном выражении в скобках стоит смешанное произведение трёх векторов. Тогда:

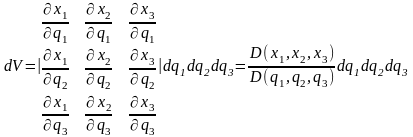. (4)

Из выражений (3) и (4) получаем выражение для коэффициентов Ламе:

.
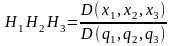