§20. Поток векторного поля. Дивергенция. Формула Остроградского-Гаусса в векторной форме.

Пусть - векторное поле, заданное в области , - регулярная двухсторонняя поверхность, содержащаяся в , - единичный вектор нормали к некоторой стороне поверхности.

Потоком векторного поля через поверхность в направлении вектора называется:

.

Пусть поверхность - замкнута и - вектор внешней нормали. Если 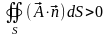, то внутри объёма, ограниченного поверхностью , имеются источники, если 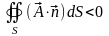- то имеются стоки.

Дивергенцией или расходимостью векторного поля в точке называется:

,

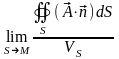где 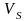- объём тела, ограниченного поверхностью . Дивергенция обозначается как .

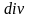Гидромеханический смысл дивергенции – это наличие в точке источника или стока и их интенсивность.

Теорема: Пусть векторное поле задано в прямоугольной декартовой системе координат. Тогда:

,

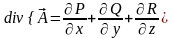при условии, что функции имеют соответствующие производные.

Доказательство.

Рассмотрим интеграл 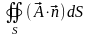. Имеем:

.

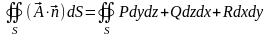Согласно формуле Остроградского получаем:

.

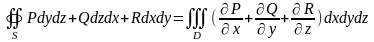Используя теорему о среднем, имеем:

. что и требовалось доказать.

Используя теорему, можно записать формулу Остроградского-Гаусса в инвариантной форме:

.

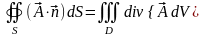§21. Циркуляция и завихренность векторного поля. Ротор. Формула Стокса в векторной форме.

Согласно определению, работа силы вдоль контура есть:

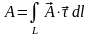, где - единичный вектор касательный к .

Циркуляцией векторного поля вдоль замкнутой линии называется работа, выполненная полем при обходе этой линии ( ).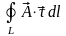

Пусть векторное поле задано в виде . Тогда имеем выражение для циркуляции векторного поля:

.

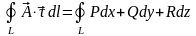Используя формулу Стокса, получаем:

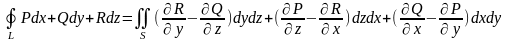, (1)

если функции , , имеют непрерывные частные производные первого порядка.

Обозначим 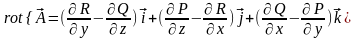вектор, который в дальнейшем будем называть ротором или вихрем векторного поля . Тогда из (1) получаем:

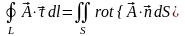. (2)

Докажем инвариантность этого определения.

Мы будем исходить, из того, что криволинейный интеграл не зависит от выбора системы координат. Возьмём плоский контур , а в качестве - участок плоскости, ограниченный контуром . Тогда вектор будет постоянный. Поэтому, используя формулу (2) и применяя теорему о среднем, получаем:

,

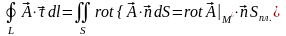где 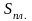- площадь . Отсюда имеем, что:

.

Если стягивать контур в точку так, что бы он всё время оставался в одной плоскости, то и точка 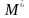переместится в точку , то есть:

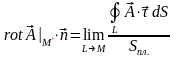. (3)

Из (3) следует, что проекция ротора на вектор не зависит от выбора системы координат, так как в правой части выражение не зависит от выбора системы координат. Так как - произвольный вектор, то и ротор не зависит от выбора системы координат, что и требовалось доказать.

Таким образом, формула (2) представляет собой формулу Стокса в векторной форме.

Для вычисления ротора в прямоугольной декартовой системе координат пользуются следующей символической формулой:

.

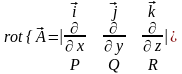Физический смысл ротора.

Пусть - векторное поле скоростей стационарного течения несжимаемой жидкости. Поместим в жидкость малое колёсико радиуса (см. рис. 22). Рассчитаем скорость вращения колеса:

,

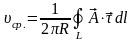
где - обод колеса. Имеем:

,

где - плоскость колеса. Согласно теореме о среднем получаем:

.

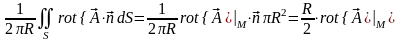Очевидно, что 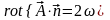, где 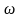- угловая скорость ( направлен по оси вверх).

Если векторы и коллинеарные, то

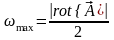
то есть ротор указывает положение оси, в котором скорость вращения колеса максимальна.