31.Решение системы линейных уравнений с помощью определителей.Формулы крамера

• Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.

• Предположим, что │А│не равен нулю, тогда существует обратная матрица А^-1.

• Умножая слева обе части матричного равенства на обратную матрицу А^-1 получим:

• А^-1 (АХ)= А^-1 В.

Решением системы уравнений методом обратной матрицы будет матрица-столбец:

Х= А^-1В.

(А^-1 А)Х =ЕХ =Х

• Т 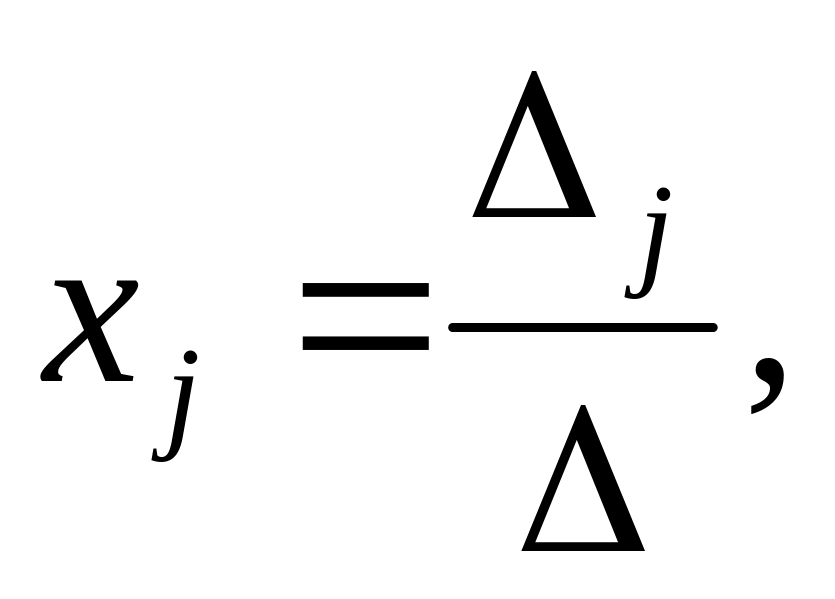еорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ_j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:

где j=1..n.

32.Решение системы линейных уравнений в матричной форме

Ма́тричный метод решения систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

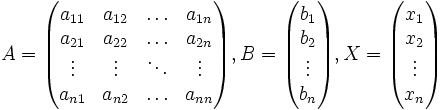
Умножим это матричное уравнение слева на A - 1 — матрицу, обратную к матрице A:

Так как A − 1A = E (учитывая ассоциативность матричного произведения), получаем X = A - 1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, т.е. когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (т.е. ненулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма

33.Решение системы линейных урав-й методом гаусса

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.

Рассмотрим матрицу:

эта матрица называется расширенной матрицей

системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.

Покажем, как методом Гаусса можно решить следующую систему:

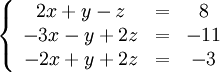
Обнулим коэффициенты при Х во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на-3\2 и -1 , соответственно:

Теперь обнулим коэффициент при У в третьей строке, вычтя из неё вторую строку, умноженную на 4:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем: Z=-1 из третьего;

Y=3 из второго, подставив полученное Z, X=2 из первого.Таким образом исходная система решена.