29. Гармонический осциллятор. Примеры: Пружинный, математический, физический маятники.

Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида d2s/dt2 + ω02s = 0 или (1)

где две точки сверху означают двукратное дифференцирование по времени. Колебания гармонического осциллятора есть важный пример периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. В качестве примеров гармонического осциллятора могут быть пружинный, физический и математический маятники, колебательный контур (для токов и напряжений настолько малых, что можно было бы элементы контура считать линейными).

Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или

Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой (2) и периодом (3)

Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна

Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела

физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом где введена величина L=J/(ml) — приведенная длина физического маятника.

Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника где l — длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то

Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.

30. Представление колебаний в виде векторов.

31. Сложение колебаний одного направления и перпендикулярных колебаний.

Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты

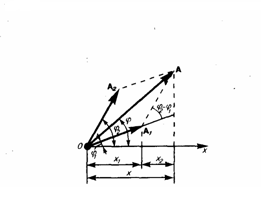
Tax как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ2 - φ1) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет

(1)

В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями (2)

Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2 - φ1) складываемых колебаний.

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это - уравнение эллипса. При A1=A2 - окружность, при (m - целое) - отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.