19. Абсолютно упругий/неупругий центральный удар.

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется.

Абсолютно неупругий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

20. Взаимосвязь между потенциальной энергией и силой взаимодействия: сила – градиент потенциальной энергии. Понятия потенциальной ямы и потенциального барьера.

Потенциа́льный барье́р — область пространства, разделяющая две другие области с различными или одинаковыми потенциальными энергиями. Характеризуется «высотой» — минимальной энергией классической частицы, необходимой для преодоления барьера.

Потенциальная яма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.

21. Потенциальное поле. Характеристики и свойства гравитационного поля. Принцип суперпозиции полей.

Потенциальное поле - это поле, в котором работа силы не зависит от формы пути, а зависит лишь от положений начальной и конечной точек траектории, а силы, действующие в нем - консервативными. В потенциальном поле работа сил по любому замкнутому контуру равна нулю.

Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

22. Неинерциальная система отсчёта: силы инерции, второй закон ньютона в неинерциальной системе, динамика абсолютно твёрдого тела.

Неинерциальная система отсчёта — всякая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчёта.

Сила инерции — векторная величина, равная произведению массы материальной точки на её ускорение и направленная противоположно ускорению. Частными случаями такой силы инерции являются центробежная сила и сила Кориолиса. Кроме того, силу инерции применяют для формальной возможности записывать уравнения динамики как более простые уравнения статики.

23. Теоремы динамики для простейших видов движения твёрдого тела: динамика поступательного движения тела, динамика вращательного движения тела вокруг неподвижной оси.

Поступательным движением ТТ называется такое движение, при котором любая прямая,

жестко связанная с телом, остается при (перемещении) движении его параллельной самой себе.

Для описания поступательного движения ТТ достаточно знать, как движется одна из его

точек. Все остальные точки движутся таким же образом.

24. Примеры расчёта осевых моментов инерции.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

где:

mi — масса i-й точки,

ri — расстояние от i-й точки до оси.

25. Уравнение динамики вращательного движения относительно оси.

При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями.

Iε = M.

26. Кинетическая энергия тела при поступательном и вращательном движении.

27. Движение тел с переменной массой. Уравнение Мещерского. Фолмула Циолковского.

Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).

Пусть в момент времени t масса ракеты m, а ее скорость v; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины v+dv. Изменение импульса системы за время dt будет равно:

где u - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:

Если на систему действуют внешние силы, то или dp = Fdt. Тогда Fdt = mdv + udm, или (2.12) где член называют реактивной силой Fp. Если вектор u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится.

Таким образом, уравнение движения тела переменной массы имеет следующий вид: (2.13)

Уравнение (2.13) называется уравнением И.В. Мещерского.

Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая F = 0 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим: откуда или где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени v=0, а стартовая масса ракеты составляет m0, то C = u*ln m0. Следовательно, (2.14)

Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:

а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0;

б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.

Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости v и u намного меньше скорости света c.

28. Дифференциальное уравнение гаронических колебаний и его решение. Определение амплитуды и начальной фазы по начальным условиям.Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса: или гдеA - амплитуда; ω - круговая частота; α - начальная фаза; ( ωt + α ) - фаза.

Фаза колебания - это аргумент гармонической функции: ( ωt + α ). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.

Амплитуда колебанияA - это наибольшее значение колеблющейся величины.

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) +α = ωt + α + 2π, или ωT = 2π.

Время T одного полного колебания называется периодом колебания. Частотойν называют величину, обратную периоду

Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1. Так как то

Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно:

График гармонического колебания:

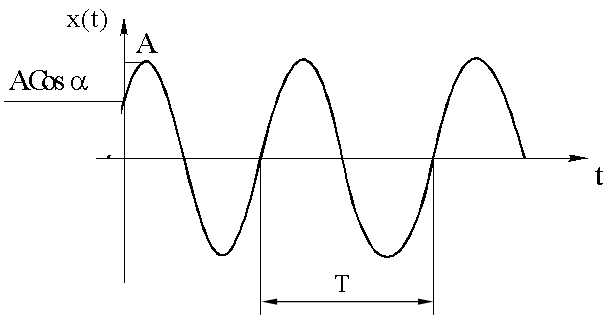
Дифференциальное уравнение гармонических колебаний:

колебания грузика, прикрепленного к пружине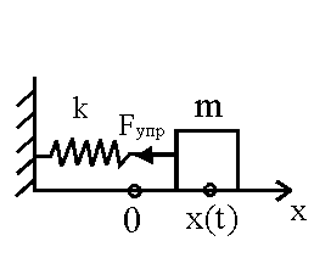

x - координата грузика

колебание физического маятника - любого тела, совершающего колебания вокруг горизонтальной оси, не проходящей через его центр тяжести

φ - угол отклонения

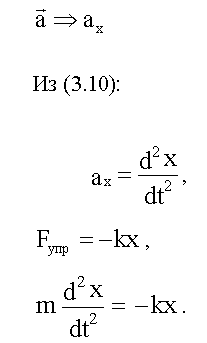
Мы получили дифференциальные уравнения, описывающие движения наших систем. В первых двух случаях уравнения одинаковы по форме, в третьем случае второй член уравнения содержит не φ, а Sin φ . Если рассматривать только малые отклонения маятника от положения равновесия, то тогда, при φ<< 1, Sin φ ≈ φи мы имеем:

Введем обозначения:

Решение дифференциального уравнения:

Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество. Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид: т.е. является гармонической функцией. Значит уравнение это дифференциальное уравнение гармонических колебаний.