Теория механизмов и машин

1. анализ и синтез механизмов .

Основные понятия и определения.

Теория машин и механизмов

Теория машин и механизмов (ТММ) — это научная дисциплина об общих методах исследования, построения, кинематики и динамики механизмов и машин и о научных основах их проектирования.

Машин и механизмов теория, наука об общих методах исследования и проектирования машин и механизмов. Наиболее развита часть науки, называемая теорией механизмов, в которой изучаются преимущественно свойства механизмов, являющиеся общими для всех (или для определённых групп) механизмов независимо от конкретного назначения машины, прибора или аппарата. Например, один и тот же механизм для преобразования вращательного движения, выполненный в виде зубчатых колёс, может применяться в автомобиле, часах, мешалках аппаратов химического производства. Во всех указанных случаях требуется одно и то же преобразование движения, поэтому методы исследования и проектирования этих механизмов имеют много общего и составляют содержание теории механизмов. Другую часть науки составляет теория машин, в которой рассматриваются методы исследования и проектирования, являющиеся общими для машин различных областей техники. Обе части науки неразрывно связаны между собой, так как механизмы составляют основу почти любой машины.

Задачи теории машин и механизмов очень разнообразны, но важнейшие из них можно сгруппировать по трём разделам: синтез механизмов, динамика машин и механизмови теория машин-автоматов. Под синтезом механизмов понимается та часть их проектирования, которая относится к выбору схемы и нахождению параметров этой схемы, обеспечивающих выполнение требуемых движений. Задачи динамики механизмов состоят в исследовании движения отдельных частей (звеньев) механизма под действием внешних сил. Теория машин-автоматов рассматривает методы построения их схем по условиям согласованности работы отдельных механизмов и достижения оптимальной производительности, точности и надёжности машин-автоматов. Разделение задач теории машин и механизмов на указанные три раздела в некоторой мере условное. Например, в синтезе механизмов учитываются не только кинематические, но и динамические условия; в динамике механизмов на основе исследования движения звеньев механизма даются рекомендации по выбору параметров механизма из условий получения оптимальных динамических характеристик, то есть выполняется динамический синтез; в теории машин-автоматов выбор исполнительных механизмов и их параметров основывается на методах синтеза механизмов, а критерии оптимальности схемы машины-автомата (в особенности схемы управления) часто определяются по динамическим показателям. Однако обзор проблем науки о машинах и механизмах по этим разделам даёт достаточно полное представление о её содержании.

Основы синтеза механизмов в его аналитической форме были заложены в 19 веке в работах русского математика и механика П. Л. Чебышева. Исследуя его работы, можно представить всю последовательность решения задач синтеза механизмов в виде трёх этапов. Первый этап — выбор основного критерия синтеза и ограничивающих условий. Каждый механизм в зависимости от назначения и условий эксплуатации должен удовлетворять ряду требований, разнообразных по форме и содержанию. Некоторые из этих требований могут быть даже противоречивыми. Однако всегда можно установить, какое требование является решающим для правильной работы механизма, и в соответствии с этим выбрать основной критерий, по которому оценивается его качество. Основной критерий синтеза является функцией параметров механизма (называется также функцией-критерием, или целевой функцией), остальные требования к нему формулируются в виде ограничивающих условий на параметры. Другими словами, первый этап решения любой задачи синтеза — этап, на котором происходит формализация требований, предъявляемых к нему. На этом этапе задачи технологические и конструктивные превращаются в математические. Второй этап — установление аналитического выражения функции, характеризующей величину основного критерия синтеза. Выбор основного критерия определяется назначением механизма. Для некоторых механизмов его аналитическое выражение может оказаться очень сложным. Между тем существуют функции, которые имеют более простой вид и в то же время с достаточной для практики точностью характеризуют величину основного критерия. При этом необходимо только, чтобы погрешности от замены функции-критерия её приближённым выражением были меньше тех погрешностей, которые возникают в реальном механизме из-за неточностей изготовления его деталей, упругости звеньев и других причин. Третий этап — вычисление постоянных параметров механизма из условий оптимизации основного критерия с учётом ограничивающих условий (ограничений). В одних случаях эти условия выражаются в виде одного или нескольких уравнений и системы неравенств, из которых непосредственно находятся искомые параметры (точный синтез). В других случаях отыскиваются такие значения параметров, при которых отклонение функции-критерия от оптимального значения является достаточно малой величиной, удовлетворяющей условиям практического использования механизма (приближённый синтез). Для приближённого синтеза Чебышев предложил оригинальный метод вычисления искомых параметров механизма, который привёл в дальнейшем к созданию математической теории приближения функций.

Указанные три этапа синтеза механизмов составляют основное содержание задачи при их проектировании, так как все последующие операции по расчёту на прочность деталей и по установлению конструктивных форм уже не могут существенно изменить его кинематических и динамических свойств. Дальнейшее развитие методов синтеза механизмов в работах русских учёных А. П. Котельникова (1865—1944), В. В. Добровольского (1880—1956) и других отечественных и зарубежных учёных состояло в отыскании наиболее целесообразных методов выполнения отдельных этапов синтеза и применения их к различным видам механизмов (с гидравлическими и электрическими устройствами, пространственные со сложным движением рабочего звена, самонастраивающиеся механизмы и т. п.). При этом выяснилось, что в простейших случаях можно удовлетворить требованиям, предъявляемым к основному критерию и ограничивающим условиям, используя несложные графические методы. Однако применение этих методов не избавляет от необходимости решать задачу синтеза в нескольких вариантах для получения результата, близкого к оптимальному. Только появление ЭВМ дало возможность эффективно и быстро выполнять третий этап синтеза, определяя оптимальные сочетания параметров механизма и даже решая такие задачи синтеза, которые ранее не могли быть решены из-за сложности и трудоёмкости вычислений. В 1965—72 для типовых задач синтеза механизмов были составлены программы вычислений на ЭВМ, позволяющие оптимизировать различные критерии и учитывать большое количество кинематических, динамических и конструктивных ограничений.

Раздел динамики механизмов иногда называется динамикой машин, так как учёт динамических явлений, происходящих в механизмах, имеет первостепенное значение при проектировании машин. В первых работах по динамике машин, выполненных Н. Е. Жуковским и Н. И. Мерцаловым (1866—1948), использовалась только механика твёрдого тела применительно к механизмам с жёсткими звеньями. После внедрения в машины новых механизмов с гидравлическими, а затем и с пневматическими устройствами (1930—50) динамика машин стала опираться не только на механику твёрдого тела, но и на механику жидкостей и газов (см. Механика). В связи с существенным ростом нагруженности и быстроходности машин и повышением требований к их качеству значительно изменилось содержание задач динамики машин: появилась необходимость учитывать упругие свойства звеньев, зазоры в подвижных соединениях, переменность масс и моментов инерции и т. п. Особое внимание стало уделяться развитию методов теории колебаний механических систем в применении к реальному механизму с его упругими и не вполне упругими элементами, зазорами, сухим трением и смазкой, наличием сложных закономерностей деформирования материалов и т. п. Изучалось и продолжает изучаться вредное действие колебаний, вызывающих увеличение нагрузок на звенья механизма, потерю устойчивости, усталостные поломки, недопустимое изменение предписанного закона движения. Вместе с тем возможно и полезное применение колебаний в вибрационных машинах, для которых колебательное движение рабочего органа составляет основное движение, заданное назначением машины. К этим машинам принадлежат, например, вибротранспортёры, вибросортировочные машины, вибромашины для забивки свай и др. Решение новых задач динамики машин основывается на развитии методов аналитической механики и нелинейной теории колебаний, механики переменной массы и теории упругости. Особое значение для решения этих задач имеют те методы, которые позволяют достаточно эффективно и быстро без интегрирования систем дифференциальных уравнений получать динамические критерии для расчёта механизмов по частотам и амплитудам установившихся колебаний, для определения границ устойчивости и т. п.

Теория машин-автоматов сравнительно недавно (1945—50) стала рассматриваться как одна из важнейших частей теории машин и механизмов. Машины-автоматы отличаются от неавтоматизированных машин в первую очередь тем, что последовательность работы отдельных механизмов, включая механизмы загрузки и выгрузки, задаётся системой управления. Поэтому развитие теории машин-автоматов связано с совершенствованием методов построения схем управления по выбранному критерию оптимальности, например по условию получения минимального числа элементов, составляющих схему. Наибольшее распространение получили методы, основанные на применении алгебры-логики, и соответственно этот раздел теории машин-автоматов получил название логического синтеза систем управления. В системах управления наряду с электрическими элементами стали применяться пневматические, обладающие, как правило, большей надёжностью. Развитие методов построения систем управления машинами-автоматами привело к созданию систем программного управления, в которых программа требуемых перемещений выражается в форме чисел (цифр) — элементарных (малых) шагов. Для реализации этих шагов предусматривают специальные типы двигателей, называемые шаговыми электродвигателями. Особую ценность имеют самонастраивающиеся и адаптирующиеся системы программного управления, в которых программа автоматически корректируется с учётом опыта предшествующих циклов работы системы и условий, в которых должна работать эта система.

Последним достижением теории машин-автоматов является разработка методов проектирования роботов, то есть машин-автоматов, моделирующих свойства и функции живых организмов и, в частности, имитирующих действия человека при перемещении в пространстве орудий и объектов труда. По своей схеме робот во многом тождествен манипулятору (механической руке), который применяется для работы в вакууме, под водой и в агрессивных средах. Исполнительные органы манипуляторов способны совершать сложные пространств, движения, необходимые для выполнения рабочих операций. Для управления действиями манипуляторов и роботов используются современные методы и средства вычислительной техники, позволяющие оперативно составлять и менять программы движений. В сочетании со станками, контрольными и сборочными автоматами, оснащенными системами программного управления, применение роботов способствует комплексной автоматизации производства. Их применение придаёт системам машин-автоматов гибкость и приспосабливаемость к изменяющимся условиям производства. При проектировании роботов и манипуляторов используются в едином комплексе методы теории машин и механизмов и теории управления. Применительно к проектированию роботов и автоматических манипуляторов развиваются как общие методы — структурный синтез пространств, незамкнутых кинематических цепей, кинематика и динамика пространств, механизмов со многими степенями свободы, теория механизмов с переменной структурой, изменяющейся в процессе движения, так и методы решения задач, относящихся только к манипуляторам, — создание манёвренности, устойчивости в работе, выбор правильного соотношения полезных и холостых ходов, а также проектирование таких систем, в которых оператор чувствует усилие, создаваемое на рабочем органе или на захвате.

По всем трём указанным разделам теории машин и механизмов ведётся интенсивная работа во многих странах. В СССР, США, ГДР, СРР, ЧССР и ФРГ систематически (через 2—3 года) проводятся национальные конференции по проблемам этой науки. Для организации и проведения международных совещаний и конгрессов по теории машин и механизмов, а также для обмена опытом и проведения совместных работ (в первую очередь по терминологии, стандартизации, теории манипуляторов и по проблемам высшего образования) в 1969 создана Международная организация по теории машин и механизмов).

Теория механизмов - наука, изучающая методы анализа и синтеза механизмов. Синтез механизма проводится с использованием результатов анализа механизмов известной структуры.

Методы анализа подробно освещаются в трёх разделах:

а) структурный анализ;

б) кинематический анализ;

в) динамический анализ.

2.2. Структурный анализ механизмов.

В задачи структурного анализа входят такие подвопросы, как определение структуры состава механизма, классификация подвижных соединений звеньев - кинематических пар и определение степени подвижности механизма. Причём причины, приводящие в движение звенья, не рассматриваются.

Итак, механизм - это замкнутая кинематическая цепь, обладающая определенностью перемещений звеньев, т.е. при задании перемещения ведущего звена (или звеньев) все остальные - ведомые - получают вполне определенные перемещения. Структура механизма состоит из отдельных частей звеньев, соединенных друг с другом подвижно с помощью кинематических пар. Все неподвижные детали М считают одним звеном - стойкой. Среди подвижных звеньев различают ведущие - положения или перемещения их в каждый момент времени задают с помощью обобщенных координат, ведомые, положения и перемещения которых однозначно зависят от положений или перемещений ведуших.

Кинематические цепи

Кинематическая классификация КП.

Кинематической парой принято называть соединение двух звеньев, обеспечивающее их определенное относительное перемещение. Звенья, объединенные КП в связанную систему, образуют кинематическую цепь.

Классифицируя кинематические пары, стоит отметить, что по характеру относительных перемещений звеньев все пары делят на 5 классов. Класс пары определяется числом условий связи, наложенных на относительное перемещение звеньев: s = 6 - w, где 6 - число независимых перемещений свободного звена, w - число относительных независимых перемещений звеньев в паре. В винтовой паре 5-го класса линейное перемещение вдоль оси винта и вращательное вокруг нее связаны и образуют одно перемещение по винтовой линии.

Определение степени подвижности механизма.

Степень подвижности М - число независимых перемещений, которые нужно сообщить его ведущим звеньям, чтобы перемещения ведомых были однозначно определены.

Степени подвижности механизма определяется по структурным формулам. Структурная формула механизма - уравнение, отражающее структуру и позволяющее определить степень подвижности:

w = 6k - sum[i* (p)i]1, 5 + qs, (2.1)

где 6k - сумма подвижностей k свободных звеньев, обьединяемых в M; sum[i* (p)i]1, 5 - сумма связей, образующихся в i парах класса (p)i (от 1 до 5 класса);

qs - дополнительные подвижности в M, обусловленные спецификой его структуры.

Подвижности qs появляются в механизме в случае, когда перемещения части звеньев совершаются по одним и тем же поверхностям. Тем не менее общие ограничения позволяют звеньям перемещаться относительно друг друга, т.е. становится пассивными. Это равносильно появлению в M дополнительных подвижностей.

Степень подвижности многоконтурного M .

Сложные механизмы часто содержат несколько связанных замкнутых кинематических цепей - контуров, в каждом из которых может быть различное число ограничений. Для таких M степень подвижности определяется по формуле

w = (6 - qs/c) *k - sum (i- qs/c) * (p)i, (2.2) где c - число контуров в M .

Это уравнение получается из (2.1) и условия k = sum[ (p)i] - c, справедливого для любого M . Например, для двухконтурного M на рис. 2.5 а, в контуре 1 q1 = 0, в контуре 2 q2 = 2 и qs = 2, следовательно, w = (6 - qs/c) *k - sum (i- qs/c) * (p)i = 5*7 - 4*7 - 3*1 - 2*1 = 2.

В M на рис. 2.5 б, который подобен рассмотренному, но имеет q1 = 2, q2 = 3, qs = 5 :

w = (6 - qs/c) *k - sum (i- qs/c) * (p)i == (6 - 5/2) *7 - (5 - 5/2) *9 = 2.

Степень подвижности этих M w = 2, т.е. у них должно быть два ведущих звена в каждом (например, звенья 1 и 7)

Пассивные звенья в механизмах

Как уже было сказано выше, подобные звенья в механизме дублируют друг друга и вводятся для повышения жесткости конструкции. При определениии степени подвижности такие звенья и соответствующие им КП не рассматривают.

Классификация механизмов

Механи́зм (греч. μηχανή mechané — машина) — это совокупность совершающих требуемые движения тел (обычно — деталей машин), подвижно связанных и соприкасающихся между собой. Механизмы служат для передачи и преобразования движения.

Механизм паровой машины имеет одну степень свободы.

Дифференциал автомобиля — механизм с двумя степенями свободы.

Механизм характеризуется числом степеней свободы — минимальным количеством его точек, кинематические характеристики которых (траектории и скорости движения) однозначно определяют траектории и скорости всех остальных точек механизма. Так, для механизма с одной степенью свободы можно найти одну точку, заданная траектория и скорость которой однозначно определяют траектории и скорости движения всех остальных его точек. Для механизма с двумя степенями свободы таких точек должно быть две[1], и т. д.

Как преобразователь движения механизм видоизменяет скорости, или траектории, или же и то, и другое. Он преобразует скорости, если при известной скорости одной из его частей другая его часть совершает движение, подобное движению первой, но с другой скоростью. Механизм преобразует траекторию, если, в то время как одна из его точек описывает известную траекторию, другая описывает другую заданную траекторию. Определенность движения механизма достигается попарным соединением его частей. Если требуется поставить тело A в такие условия, чтобы оно могло проходить последовательно только через определенные положения, то определяют поверхность, касательную ко всем этим положениям тела A (такая поверхность называется огибающей) и делают в неподвижном теле B канал, имеющий форму найденной огибающей. Тело A, помещённое в такой канал, будет способно только к определённому движению. Элементы механизмов

Такая совокупность двух тел, в которой формой одного тела определяется весь ряд последовательных положений, которые способно в нём занять другое тело, называется кинематической парой. Тела, составляющие пару, называются её звеньями. Например, тело, имеющее призматический канал, и помещенная в этом канале призма составляют поступательную пару, потому что одно из этих тел может совершать относительно другого только поступательное движение. Цилиндрическая втулка и помещенный в ней шип, снабженный закраинами, не дающими ему выскочить из втулки, составляют вращательную пару. Винт и гайка составляют винтовую пару. Расстояние между нарезками винта, считаемое по направлению оси винта, называется его шагом, так что, обойдя винт один раз, нарезка приближается к концу винта на один шаг. Поступательная пара может быть математически рассматриваема как такая винтовая, шаг которой равен бесконечности. Вращательная пара может быть рассматриваема как винтовая, шаг которой равен нулю. Эти пары называются простыми; отличительное свойство их заключается в том, что в них относительное движение одного звена по отношению к другому тождественно с относительным движением второго звена по отношению к первому.

Пары, не обладающие этим свойством, называются высшими. Таковы: зацепляющиеся между собой зубчатые колеса, шкив и перекинутый через него ремень, дуговой двухсторонник и полая трёхгранная призма и многие другие.

Движение звена A в звене B называется обращенным по отношению к движению звена B в звене A. Одну из наиболее интересных высших пар представляет собой эллиптический циркуль. Он состоит из доски, в которой сделаны два крестообразно пересекающихся между собой прямолинейных, перпендикулярных друг к другу прореза, и из стержня с выступающими на концах цилиндрическими шипами, диаметры которых равны ширине прорезов. Стержень вставляется шипами в прорезы так, чтобы один шип ходил по одному, а другой по другому из прорезов; с противоположной стороны на шипы навинчиваются винты с головками, препятствующими шипам выскочить из прорезов. При неподвижности доски траектория всех точек стержня суть эллипсы; как частные случаи эллипсов траектория центров шипов суть прямые линии, а траектория середины стержня — окружность. Движение стержня относительно доски происходит так, как будто бы соединённый с ним круг, построенный на нём как на диаметре, катился по внутренней стороне окружности, описанной из точки пересечения средних линий прорезов радиусом, равным диаметру катящегося круга. В обращенном движении, то есть при неподвижности стержня, все точки доски описывают улитки Паскаля (см. Кривые).

Звено B, соединённое в какую-либо пару со звеном A, может быть соединено в пару же со звеном C, которое, в свою очередь, может составлять пару со звеном D и так далее. Такое последовательное соединение звеньев в пары называется кинематической цепью. Если последнее звено кинематической цепи соединено в пару с первым, то цепь называется замкнутой, в противном случае она называется открытой. Такая кинематическая замкнутая цепь, которая при неподвижности одного из звеньев получает определенность движения, характеризующую механизм, называется принудительной. Когда в принудительной цепи одно из звеньев предполагается неподвижным, то говорят, что цепь поставлена на этом звене. Ставя принудительную цепь последовательно на разные её звенья, получим столько механизмов, сколько имеется звеньев в цепи. Примером принудительной цепи может служить шарнирный четырёхсторонник, состоящий из четырёх стержней, соединённых между собой вращательными парами, называемыми шарнирами.

Механизм, все точки которого описывают траектории, лежащие в параллельных между собой плоскостях, называется плоским. Движение твердого тела, в котором все точки его описывают траектории, параллельные одной и той же плоскости, называется также плоским. Всякое плоское движение происходит так, как будто бы некоторая кривая, соединённая неизменяемо с движущимся телом, катилась по некоторой другой неподвижной кривой. Эти кривые называются полодиями. Полодии, как катящиеся друг по другу кривые, постоянно прикасаются одна к другой. Их общая точка прикосновения называется мгновенным полюсом. В течение весьма малого промежутка времени движение тела можно рассматривать как бесконечно малое вращение около мгновенного полюса. Так, например, в описанном выше эллиптическом циркуле движение, как мы видели, приводится к катанию одного круга по другому; эти круги и есть суть полодии данного движения. Если бы весь эллиптический циркуль (и доска, и стержень) был подвижен, то все-таки относительное движение стержня и доски было бы то же самое и определялось бы катанием тех же полодий. Относительное движение каждых двух звеньев принудительной цепи, хотя бы эти звенья и не были соседними, составляя пару, характеризуется катанием двух соответствующих полодий (в плоском механизме). Всякое движение твердого тела (не плоское) приводится к катанию друг по другу, соединённому со скольжением, двух линейчатых поверхностей, называемых аксоидами.

Зубчатые колёса

Наибольшим практическим значением из всех высших пар пользуются зубчатые колёса, представляющие собой необходимое для преодоления более или менее значительных сопротивлений видоизменение катков. Цилиндрическими катками называются цилиндрические твёрдые тела, вращающиеся около своих геометрических осей и прикасающиеся друг к другу своими боковыми поверхностями, которые делаются шероховатыми. Если вращать один из таких катков, то благодаря существующему между катками трению и другой будет вращаться. Скорости вращения были бы обратно пропорциональны радиусам, если бы катки не скользили один по другому. Полодиями относительного движения двух соприкасающихся катков служат окружности основания самих катков. Чтобы устранить скольжение полодий, можно было бы на каждом из катков сделать впадины и выступы, чтобы выступы одного входили во впадины другого. Это и будут зубчатые колеса.

Полодии двух зацепляющихся между собой зубчатых цилиндрических (лобовых) колес суть окружности, называемые начальными. Отношение угловых (вращательных) скоростей обратно пропорционально радиусам начальных окружностей. Впадины и выступы зубчатого колеса образуют зубцы. Расстояние между двумя соответственными точками пересечения профилей двух соседних зубцов с начальной окружностью, считаемое по этой окружности, называется шагом. Приготовление зубчатого колеса начинается с того, что начальную окружность его, размер которой определяется по данной относительной скорости колеса, делят на столько равных частей, сколько зубцов предполагается сделать на колесе; расстояние между соседними точками деления и будет равно шагу. Шаги сцепляющихся колес должны быть равны между собой, а, следовательно, радиусы начальных окружностей пропорциональны числам зубцов. Если полодии относительного движения двух зубчатых колёс суть окружности, то отношение скоростей обратно пропорционально радиусам полодий и, следовательно, постоянно; такое постоянство и требуется от правильно устроенных колёс, а так как в зубчатых колёсах полодии ничем не отмечены, то сама форма зубцов должна быть такова, чтобы при сцеплении их относительное движение колёс характеризовалось бы круговыми полодиями данных радиусов.

Существует несколько способов определения правильной формы зубцов, удовлетворяющих этому условию. Все эти способы основаны на следующем соображении. Пусть дан профиль зубца колеса A; покатим начальную окружность колеса A по начальной окружности колеса B на один шаг и найдем огибающую ко всем положениям, принимаемым при этом данным зубцом; эта огибающая и будет, по общему методу построения пар, представлять собой искомую форму зубца колеса B. Способ этот приложим к определению вида зубца колеса B в том случае, когда профиль зубца колеса A есть маленькая окружность, описанная из точки деления начальной окружности радиусом, раза в четыре меньшим шага; такое колесо называется цевочным и имеет зубцы, называемые цевками, в виде палок, параллельных оси колеса; профили цевок суть кружки, представляющие собой сечения цевок плоскостью, перпендикулярной к оси колеса. Покатим цевочное колесо A по колесу B; при этом центр цевки опишет эпициклоиду и огибающая последовательных положений цевки будет кривая, параллельная этой эпициклоиде и отстоящая от неё на расстояние радиуса цевки. Этой кривой и нужно ограничить бок зубца колеса B. Полный зубец ограничивается двумя такими боками, расположенными симметрично относительно средней линии зубца, направленной по радиусу колеса. а) Способ рулетт. Рулеттой называется кривая, чертимая какой-нибудь точкой кривой A, катящейся по кривой B. Пусть начальные окружности M и N колес соприкасаются взаимно в точке O. Построим произвольных радиусов вспомогательные круги P и Q, из которых P имел бы внутреннее прикосновение в точке O с M, круг же Q имел бы внутреннее прикосновение тоже в точке O с N. Покатим все четыре круга один по другому так, чтобы они постоянно соприкасались бы в одной точке. Изберем на P какую-нибудь точку a. Эта точка при катании P по M опишет гипоциклоиду p и при катании P по N опишет эпициклоиду q. Кривые p и q будут в течение движения соприкасаться взаимно потому, что обе чертятся одной и той же точкой a. Если принять p за форму впадины зубца колеса M, то q будет огибающая различных положений p и, как таковая, может быть принята за профиль выступа колеса N. Выступ колеса M и впадина колеса N образуются катанием кривой Q подобным же образом. Если взять радиус вспомогательной окружности P вдвое меньшим, то (как это видно из приведенной выше теории эллиптического циркуля) гипоциклоида p получает вид прямой. б) Способ развертывающих. Пусть O есть точка соприкосновения начальных окружностей; проведем через неё прямую, наклоненную к линии центров CC' под углом 75°, опустим из центров C и C' перпендикуляры CA и C’B на эту прямую и опишем из C и C' окружности радиусами CA и C’B; вообразим себе твердые цилиндры, построенные на найденных вспомогательных окружностях, как на основаниях; обернем около цилиндра CA нитку, свободный конец которой вытянем до O, и в этом месте укрепим на нитку карандаш. Двигая карандашом направо и налево так, чтобы идущая с цилиндра нить оставалась натянутой, не скользила бы по цилиндру, а только развертывалась бы несколько с него при движении карандаша в одну сторону и навертывалась бы при движении карандаша в другую сторону, начертим кривую, называемую развертывающей (см. Кривые, табл. II, фиг. 11). Эта кривая и будет профилем зубца колеса C. Профиль зубца колеса C' получается развертыванием нити с окружности C’B. в) Кроме этих точных способов построения зубцов, существуют ещё приближенные, состоящие в нахождении круговых дуг, близко подходящих к теоретически правильным кривым. Из таких способов наиболее известны изобретенные Виллисом, Чебышевым и Петровым. Длина зубцов определяется из условия, чтобы постоянно находились в зацеплении три зубца.

Косозубые зубчатые колёса

Для того, чтобы, не увеличивая длины зубцов, дать возможность большему их числу находиться в одновременном зацеплении, поступают следующим образом: на готовое зубчатое колесо кладут так, чтобы оси их совпадали, другое такое же колесо и поворачивают его на 1/5 шага, на это колесо кладут третье и поворачивают его на 1/5 шага относительно второго и так далее накладывают одно на другое пять колёс, которые и скрепляют между собой наглухо в таком положении или, ещё лучше, отливают целиком штуку, имеющую форму таких сложенных колёс; то же делают и для того колеса, которое должно сцепляться с приготовленным таким образом колесом. Такие колёса называются ступенчатыми, так как боковые поверхности их оказываются покрытыми ступенчатыми линиями. Если бы для приготовления ступенчатого колеса мы взяли не 5 толстых колёс, отступающих друг от друга на 1/5 шага, а бесконечное множество бесконечно тонких колес, отступающих друг от друга на бесконечно малую часть шага, то на боковой поверхности получили бы не ступенчатые, а винтовые линии. Такие колёса с винтообразно идущими зубцами и отливаются (конечно целиком, а не из бесконечного числа тонких колёс, рассматриваемых только в теории). Эти колёса, по имени изобретателя называемые колёсами Гука, употребляются в механизмах, требующих большой плавности движения. При помощи именно колёс Гука знаменитый мастер Бреге устроил, для определения по мысли Араго и Физо скорости света в жидкостях, снаряд, в котором маленькое зеркальце делало до 2000 оборотов в секунду.

Применение зубчатых колес при различных взаимных положениях их осей

Цилиндрические (лобовые) колеса употребляются для передачи вращения между осями параллельными. Для передачи вращения между осями пересекающимися употребляются конические колеса, а для передачи между осями непараллельными и непересекающимися служат гиперболоидные колеса. Винт, способный вращаться около своей оси, но не имеющий поступательного движения, может быть помещен так, чтобы составлять с зубчатым колесом зацепляющуюся пару. При таком соединении на один оборот винта, называемого иногда червяком, колесо поворачивается на один свой шаг.

[править] Передаточное отношение

Если имеется ряд валов с насаженными на них наглухо последовательно зацепляющимися зубчатыми колесами, по одному колесу на каждом валу, то абсолютная величина отношения угловой скорости первого и последнего вала, сколько бы ни было промежуточных колес, будет та же самая, как если бы первое и последнее колесо зацеплялись между собой непосредственно. Если же желают изменить это отношение, как это требуется, например, при устройстве часов, то на 1-й вал насаживают колесо, сцепляющееся с маленьким колесом, называемым шестерней, насаженным на втором валу, на котором параллельно с шестерней насаживается колесо, сцепляющееся с шестерней 3-го вала, и так далее; наконец, колесо предпоследнего вала сцепляют с шестерней последнего вала. В таком механизме отношение угловых скоростей первого и последнего валов выражается формулой:

ω 1/ ω n = (-1)n-1(m1 m2 m3…mn)/(M1 M2 M3…Mn-1)

где ω 1 — угловая скорость первого вала, ω n — угловая скорость последнего вала, n — число валов, M1M2M3…— число зубцов колес, m1m2m3…— число зубцов шестерен. Множитель (-1) n-1 стоит для того, чтобы показать, что при четном числе валов первый и последний вращаются в противоположные стороны, а при нечетном числе валов — в одну и ту же сторону. Если некоторые из валов в системе зубчатых колес подвижны, то такая система называется эпициклической. Эпициклические системы представляют чрезвычайно богатый материал для преобразования вращения. Так, например, при помощи такой системы, состоящей только из четырёх колес почти одинакового размера, можно достигнуть такой передачи, при которой на 10000 оборотов некоторой части механизма другая его часть делает только один оборот.

Особый, весьма богатый класс составляют механизмы, состоящие из зубчатого колеса с острыми зубцами, круто скошенными в одну сторону и отлого в другую, и задерживающей собачки. Такие колеса называются храповыми. К этому классу относится, между прочим, соединение храпового колеса с якорем маятника в стенных часах и разные другие спуски.

КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ

3.1. Основные понятия и определения. Задачи кинематического анализа.

3.1.1. Кратко подытожив вышесказанное, имеем: кинематический анализ - раздел теории механизмов, в котором изучают движение звеньев в М, однако причины, вызывающие движение, не рассматриваются. Кинематические параметры - положение звена относительно системы координат, его скорость и ускорение. Кинематические характеристики - функции, связывающие в М параметры движения ведущего звена с параметрами движения ведомого.

Задачи кинематического анализа:

а) определение кинематических параметров звеньев М и их характер ных точек;

б) определение кинематических характеристик М.

3.2. Основные виды движения звеньев

3.2.1. Основные виды движения:

а) поступательное;

б) вращательное;

в) сложное.

Последний - общий случай движения, которое может быть представлено суммой поступательного и вращательного или как последовательность мгновенных вращательных движений.

3.2.2. Поступательное движение. Твердое тело или звено перемещается так, что любая прямая, связанная с телом, остается параллельной своему первоначальному положению (рис. 3.1) . Перемещения, скорости и ускорения всех точек звена соответственно одинаковы. Если положения любых двух точек (например, A и В) определить векторами (r) a и (r) b, то при движении вектор (r) ab = AB не меняется, т.е. скорости (v) a и (v) b равны; также равны и ускорения (w) a и (w) b .

3.2.3. Вращательное движение. Все точки звена движутся по круговым траекториям в параллельных плоскостях, а центры этих окружностей находятся на общей оси вращения (рис. 3.2) .

Вращение характеризуется угловой скоростью omega = dfi/dr и угловым ускорением eps = domega/dtau. Линейная скорость точки при вращательном движении v = (dfi/dtau) x r = omega x r . Линейное ускорение:

w = dv/dtau = (domega/dtau) x r + omega x (dr/dtau) = eps x r + omega x omega x r = (w) t + (w) n . (3.1)

Вектор тангенциального ускорения (w) t направлен по касательной к траектории движения, нормального w (n) - к центру вращения.

Модуль вектора полного ускорения

w = [ (eps*ro) **2 + ( (omega**2) *ro) **2]**0.5 = ro*[eps**2 + omega**4]**0.5, (3.2)

где ro - радиус вращения.

3.2.4. Сложное движение звена. Его обычно представляют суммой двух более простых движений: относительного в подвижной системе координат K' и переносного вместе с этой системой относительно системы координат K, которая обычно неподвижна (рис. 3.3) .

3.2.5. Скорости и ускорения при сложном движении. При сложном (абсолютном) движении приращение вектора скорости (v) a:

d (v)a = d (v)o + dfi x r' + (v) r*dtau,

следовательно, абсолютная скорость (v) a есть сумма переносной (v) e и относительной (v) r скоростей:

(v)a = (v) o + omega x r' + (v) r = (v) e + (v) r . (3.3)

Приращение вектора ускорения при сложном движении:

d (w)a = d (w)o + d (omega x r') + dfi x (v) r + (w) r*dtau ;

d (omega x r') = eps x r' + omega x omega x r' + omega x (v) r ;

dfi x (v) r = omega x (v) r.

Таким образом, ускорение при сложном движении

(w)a = (w) o + eps x r' + omega x omega x r' + 2*omega x (v) r + (w) r. (3.4)

Составляющие абсолютного ускорения:

(w)e = (w) o + eps x r' + omega x omega x r' - переносное ускорение;

(w)k = 2*omega x (v) r - ускорение Кориолиса;

(w)r - относительное ускорение.

Кинематические характеристики механизмов.

4.1.1. Кинематические характеристики - зависимости, связывающие в М положения, скорости и ускорения ведущего звена с соответствующими параметрами ведомого. Эти функции полностью определяются структурой и геометрическими параметрами М.

4.1.2. Функция положения М - зависимость положения ведомого звена от положения ведущего. В общем виде для М (рис. 4.1) :

fin = П (fi1) . (4.1)

4.1.3. Функция скорости М - связь скоростей ведомого звена omegan и ведущего omega1 - производная функции положения:

dfin/dtau = d[П (fi1) ]/dtau = {d[П (fi1) ]/dfi1}* (dfi1/dtau),

d[П (fi1) ]/dfi1= П' (fi1) = omegan/omega1 . (4.2)

Передаточное отношение - величина, обратная функции скорости:

(i)1n = omega1/omegan = 1/П' (fi1) . (4.3)

4.1.4. Функция ускорения М - связь ускорений ведомого звена epsn и ведущего eps1 - вторая производная функции положения:

d2fin/dtau2 = d|{d[П (fi1) ]/dtau}* (dfi1/dtau) |/dtau =

= П'' (fi1) * (dfi1/dtau) **2 + П' (fi1) * (d2fi1/dtau2) =

= П'' (fi1) **omega1**2 + П' (fi1) *eps1 ;

Если принять eps1 = 0, то

П'' (fi1) = d2[П (fi1) ]/dfi12 = epsn/omega1**2 . (4.4)

Следовательно, функция ускорения определяет ускорение ведомого звена М при постоянной скорости ведущего.

4.2. Методы определения кинематических характеристик.

4.2.1. Метод векторного замкнутого контура. Сущность этого аналитического метода: звенья М представляют векторами, которые должны образовать замкнутый контур, т.е. сумма проекций звеньев- векторов на оси произвольно выбранной системы координат должна быть равна нулю.

Уравнение проекций позволяет найти функцию положения, а дифференцирование ее даст функции скорости и ускорения. Для М на рис. 4.2 уравнения проекций на оси X и Z :

r*cos (fi1) + l*cos (fi2) - s = 0;

h + r*sin (fi1) - l*sin (fi2) = 0.

Функция положения

dzet = s/r = cos (fi1) +

+ [ (l/r) **2 - (h/r + sin (fi1) )**2]**0.5 (4.5)

Функции скорости и ускорения:

П' (fi1) = ddzet/dfi1 = v3/ (r*omega1) ;

П'' (fi1) = d2dzet/dfi12 = w3/ (r*omega1**2) .

4.2.2. Графоаналитический метод планов. Сущность его состоит в построении векторных диаграмм, изображающих скорости и ускорения М для одного его положения, т.е. получают мгновенные значения кинематических характеристик М. Исходным является план положений М - изображение М в масштабе при некотором положении ведущего звена (рис. 4.3 а) .

План скоростей - графическое решение векторных уравнений, связывающих скорости абсолютного, переносного и относительного движений точек звеньев (рис. 4.3 б) . Аналогично строится план ускорений (рис. 4.3 в) .

ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ

5.1. Задачи анализа; основные понятия и определения.

Задачи динамического анализа:

а) определение усилий, действующих на звенья М при его работе, или силовой анализ;

б) определение законов движения М под действием приложенных усилий, или динамика механизма.

Сила - количественная мера механического взаимодействия тел.

Система сил - совокупность сил, действующих на звено. Система может быть уравновешенной, если под действием ее тело находится в равновесии. Равнодействующая - сила, заменяющая действие системы сил. Момент силы - векторное произведение радиуса-вектора точки приложения силы на саму силу (рис. 5.1) : T = (r) a x F ; плечо силы, создающей момент (расстояние до линии действия силы) : h = (r) a*sin (alfa) .

Кинематическая цепь (англ. kinematic chain) — это связанная система объектов, образующих между собой кинематические пары.

Кинематические цепи имеют такую классификацию:

Простые и сложные. В простой кинематической цепи каждое из ее звеньев входит в состав одной или двух кинематических пар, а в сложной кинематической цепи имеются звенья, входящие в состав трех и более кинематических пар.

Открытые и замкнутые. В открытой (незамкнутой) кинематической цепи имеются звенья, входящие в состав одной кинематической пары, а в замкнутой цепи каждое звено входит в состав 2-х и более кинематических пар.

Плоские и пространственные. Если точки всех звеньев кинематической цепи двигаются в одной или параллельных плоскостях, то такая кинематическая цепь называется плоской, в противном случае кинематическая цепь — пространственная, так как точки её звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые.

В терминах вычисления прямой и инверсной кинематики сложность кинематической цепи определяется следующими факторами:

Топология: последовательная цепь, параллельный манипулятор, древовидная структура или граф.

Геометрическая форма: как граничат соединения, которые пространственно связанные друг с другом

Механи́зм (греч. μηχανή mechané — машина) — это совокупность совершающих требуемые движения тел (обычно — деталей машин), подвижно связанных и соприкасающихся между собой. Механизмы служат для передачи и преобразования движения.

Механизм паровой машины имеет одну степень свободы.

Дифференциал автомобиля — механизм с двумя степенями свободы.

Механизм характеризуется числом степеней свободы — минимальным количеством его точек, кинематические характеристики которых (траектории и скорости движения) однозначно определяют траектории и скорости всех остальных точек механизма. Так, для механизма с одной степенью свободы можно найти одну точку, заданная траектория и скорость которой однозначно определяют траектории и скорости движения всех остальных его точек. Для механизма с двумя степенями свободы таких точек должно быть две[1], и т. д.

Как преобразователь движения механизм видоизменяет скорости, или траектории, или же и то, и другое. Он преобразует скорости, если при известной скорости одной из его частей другая его часть совершает движение, подобное движению первой, но с другой скоростью. Механизм преобразует траекторию, если, в то время как одна из его точек описывает известную траекторию, другая описывает другую заданную траекторию. Определенность движения механизма достигается попарным соединением его частей. Если требуется поставить тело A в такие условия, чтобы оно могло проходить последовательно только через определенные положения, то определяют поверхность, касательную ко всем этим положениям тела A (такая поверхность называется огибающей) и делают в неподвижном теле B канал, имеющий форму найденной огибающей. Тело A, помещённое в такой канал, будет способно только к определённому движению. Элементы механизмов

Такая совокупность двух тел, в которой формой одного тела определяется весь ряд последовательных положений, которые способно в нём занять другое тело, называется кинематической парой. Тела, составляющие пару, называются её звеньями. Например, тело, имеющее призматический канал, и помещенная в этом канале призма составляют поступательную пару, потому что одно из этих тел может совершать относительно другого только поступательное движение. Цилиндрическая втулка и помещенный в ней шип, снабженный закраинами, не дающими ему выскочить из втулки, составляют вращательную пару. Винт и гайка составляют винтовую пару. Расстояние между нарезками винта, считаемое по направлению оси винта, называется его шагом, так что, обойдя винт один раз, нарезка приближается к концу винта на один шаг. Поступательная пара может быть математически рассматриваема как такая винтовая, шаг которой равен бесконечности. Вращательная пара может быть рассматриваема как винтовая, шаг которой равен нулю. Эти пары называются простыми; отличительное свойство их заключается в том, что в них относительное движение одного звена по отношению к другому тождественно с относительным движением второго звена по отношению к первому.

Пары, не обладающие этим свойством, называются высшими. Таковы: зацепляющиеся между собой зубчатые колеса, шкив и перекинутый через него ремень, дуговой двухсторонник и полая трёхгранная призма и многие другие.

Движение звена A в звене B называется обращенным по отношению к движению звена B в звене A. Одну из наиболее интересных высших пар представляет собой эллиптический циркуль. Он состоит из доски, в которой сделаны два крестообразно пересекающихся между собой прямолинейных, перпендикулярных друг к другу прореза, и из стержня с выступающими на концах цилиндрическими шипами, диаметры которых равны ширине прорезов. Стержень вставляется шипами в прорезы так, чтобы один шип ходил по одному, а другой по другому из прорезов; с противоположной стороны на шипы навинчиваются винты с головками, препятствующими шипам выскочить из прорезов. При неподвижности доски траектория всех точек стержня суть эллипсы; как частные случаи эллипсов траектория центров шипов суть прямые линии, а траектория середины стержня — окружность. Движение стержня относительно доски происходит так, как будто бы соединённый с ним круг, построенный на нём как на диаметре, катился по внутренней стороне окружности, описанной из точки пересечения средних линий прорезов радиусом, равным диаметру катящегося круга. В обращенном движении, то есть при неподвижности стержня, все точки доски описывают улитки Паскаля (см. Кривые).

Звено B, соединённое в какую-либо пару со звеном A, может быть соединено в пару же со звеном C, которое, в свою очередь, может составлять пару со звеном D и так далее. Такое последовательное соединение звеньев в пары называется кинематической цепью. Если последнее звено кинематической цепи соединено в пару с первым, то цепь называется замкнутой, в противном случае она называется открытой. Такая кинематическая замкнутая цепь, которая при неподвижности одного из звеньев получает определенность движения, характеризующую механизм, называется принудительной. Когда в принудительной цепи одно из звеньев предполагается неподвижным, то говорят, что цепь поставлена на этом звене. Ставя принудительную цепь последовательно на разные её звенья, получим столько механизмов, сколько имеется звеньев в цепи. Примером принудительной цепи может служить шарнирный четырёхсторонник, состоящий из четырёх стержней, соединённых между собой вращательными парами, называемыми шарнирами.

Механизм, все точки которого описывают траектории, лежащие в параллельных между собой плоскостях, называется плоским. Движение твердого тела, в котором все точки его описывают траектории, параллельные одной и той же плоскости, называется также плоским. Всякое плоское движение происходит так, как будто бы некоторая кривая, соединённая неизменяемо с движущимся телом, катилась по некоторой другой неподвижной кривой. Эти кривые называются полодиями. Полодии, как катящиеся друг по другу кривые, постоянно прикасаются одна к другой. Их общая точка прикосновения называется мгновенным полюсом. В течение весьма малого промежутка времени движение тела можно рассматривать как бесконечно малое вращение около мгновенного полюса. Так, например, в описанном выше эллиптическом циркуле движение, как мы видели, приводится к катанию одного круга по другому; эти круги и есть суть полодии данного движения. Если бы весь эллиптический циркуль (и доска, и стержень) был подвижен, то все-таки относительное движение стержня и доски было бы то же самое и определялось бы катанием тех же полодий. Относительное движение каждых двух звеньев принудительной цепи, хотя бы эти звенья и не были соседними, составляя пару, характеризуется катанием двух соответствующих полодий (в плоском механизме). Всякое движение твердого тела (не плоское) приводится к катанию друг по другу, соединённому со скольжением, двух линейчатых поверхностей, называемых аксоидами.

Зубчатые колёса

Наибольшим практическим значением из всех высших пар пользуются зубчатые колёса, представляющие собой необходимое для преодоления более или менее значительных сопротивлений видоизменение катков. Цилиндрическими катками называются цилиндрические твёрдые тела, вращающиеся около своих геометрических осей и прикасающиеся друг к другу своими боковыми поверхностями, которые делаются шероховатыми. Если вращать один из таких катков, то благодаря существующему между катками трению и другой будет вращаться. Скорости вращения были бы обратно пропорциональны радиусам, если бы катки не скользили один по другому. Полодиями относительного движения двух соприкасающихся катков служат окружности основания самих катков. Чтобы устранить скольжение полодий, можно было бы на каждом из катков сделать впадины и выступы, чтобы выступы одного входили во впадины другого. Это и будут зубчатые колеса.

Полодии двух зацепляющихся между собой зубчатых цилиндрических (лобовых) колес суть окружности, называемые начальными. Отношение угловых (вращательных) скоростей обратно пропорционально радиусам начальных окружностей. Впадины и выступы зубчатого колеса образуют зубцы. Расстояние между двумя соответственными точками пересечения профилей двух соседних зубцов с начальной окружностью, считаемое по этой окружности, называется шагом. Приготовление зубчатого колеса начинается с того, что начальную окружность его, размер которой определяется по данной относительной скорости колеса, делят на столько равных частей, сколько зубцов предполагается сделать на колесе; расстояние между соседними точками деления и будет равно шагу. Шаги сцепляющихся колес должны быть равны между собой, а, следовательно, радиусы начальных окружностей пропорциональны числам зубцов. Если полодии относительного движения двух зубчатых колёс суть окружности, то отношение скоростей обратно пропорционально радиусам полодий и, следовательно, постоянно; такое постоянство и требуется от правильно устроенных колёс, а так как в зубчатых колёсах полодии ничем не отмечены, то сама форма зубцов должна быть такова, чтобы при сцеплении их относительное движение колёс характеризовалось бы круговыми полодиями данных радиусов.

Существует несколько способов определения правильной формы зубцов, удовлетворяющих этому условию. Все эти способы основаны на следующем соображении. Пусть дан профиль зубца колеса A; покатим начальную окружность колеса A по начальной окружности колеса B на один шаг и найдем огибающую ко всем положениям, принимаемым при этом данным зубцом; эта огибающая и будет, по общему методу построения пар, представлять собой искомую форму зубца колеса B. Способ этот приложим к определению вида зубца колеса B в том случае, когда профиль зубца колеса A есть маленькая окружность, описанная из точки деления начальной окружности радиусом, раза в четыре меньшим шага; такое колесо называется цевочным и имеет зубцы, называемые цевками, в виде палок, параллельных оси колеса; профили цевок суть кружки, представляющие собой сечения цевок плоскостью, перпендикулярной к оси колеса. Покатим цевочное колесо A по колесу B; при этом центр цевки опишет эпициклоиду и огибающая последовательных положений цевки будет кривая, параллельная этой эпициклоиде и отстоящая от неё на расстояние радиуса цевки. Этой кривой и нужно ограничить бок зубца колеса B. Полный зубец ограничивается двумя такими боками, расположенными симметрично относительно средней линии зубца, направленной по радиусу колеса. а) Способ рулетт. Рулеттой называется кривая, чертимая какой-нибудь точкой кривой A, катящейся по кривой B. Пусть начальные окружности M и N колес соприкасаются взаимно в точке O. Построим произвольных радиусов вспомогательные круги P и Q, из которых P имел бы внутреннее прикосновение в точке O с M, круг же Q имел бы внутреннее прикосновение тоже в точке O с N. Покатим все четыре круга один по другому так, чтобы они постоянно соприкасались бы в одной точке. Изберем на P какую-нибудь точку a. Эта точка при катании P по M опишет гипоциклоиду p и при катании P по N опишет эпициклоиду q. Кривые p и q будут в течение движения соприкасаться взаимно потому, что обе чертятся одной и той же точкой a. Если принять p за форму впадины зубца колеса M, то q будет огибающая различных положений p и, как таковая, может быть принята за профиль выступа колеса N. Выступ колеса M и впадина колеса N образуются катанием кривой Q подобным же образом. Если взять радиус вспомогательной окружности P вдвое меньшим, то (как это видно из приведенной выше теории эллиптического циркуля) гипоциклоида p получает вид прямой. б) Способ развертывающих. Пусть O есть точка соприкосновения начальных окружностей; проведем через неё прямую, наклоненную к линии центров CC' под углом 75°, опустим из центров C и C' перпендикуляры CA и C’B на эту прямую и опишем из C и C' окружности радиусами CA и C’B; вообразим себе твердые цилиндры, построенные на найденных вспомогательных окружностях, как на основаниях; обернем около цилиндра CA нитку, свободный конец которой вытянем до O, и в этом месте укрепим на нитку карандаш. Двигая карандашом направо и налево так, чтобы идущая с цилиндра нить оставалась натянутой, не скользила бы по цилиндру, а только развертывалась бы несколько с него при движении карандаша в одну сторону и навертывалась бы при движении карандаша в другую сторону, начертим кривую, называемую развертывающей (см. Кривые, табл. II, фиг. 11). Эта кривая и будет профилем зубца колеса C. Профиль зубца колеса C' получается развертыванием нити с окружности C’B. в) Кроме этих точных способов построения зубцов, существуют ещё приближенные, состоящие в нахождении круговых дуг, близко подходящих к теоретически правильным кривым. Из таких способов наиболее известны изобретенные Виллисом, Чебышевым и Петровым. Длина зубцов определяется из условия, чтобы постоянно находились в зацеплении три зубца.

Косозубые зубчатые колёса

Для того, чтобы, не увеличивая длины зубцов, дать возможность большему их числу находиться в одновременном зацеплении, поступают следующим образом: на готовое зубчатое колесо кладут так, чтобы оси их совпадали, другое такое же колесо и поворачивают его на 1/5 шага, на это колесо кладут третье и поворачивают его на 1/5 шага относительно второго и так далее накладывают одно на другое пять колёс, которые и скрепляют между собой наглухо в таком положении или, ещё лучше, отливают целиком штуку, имеющую форму таких сложенных колёс; то же делают и для того колеса, которое должно сцепляться с приготовленным таким образом колесом. Такие колёса называются ступенчатыми, так как боковые поверхности их оказываются покрытыми ступенчатыми линиями. Если бы для приготовления ступенчатого колеса мы взяли не 5 толстых колёс, отступающих друг от друга на 1/5 шага, а бесконечное множество бесконечно тонких колес, отступающих друг от друга на бесконечно малую часть шага, то на боковой поверхности получили бы не ступенчатые, а винтовые линии. Такие колёса с винтообразно идущими зубцами и отливаются (конечно целиком, а не из бесконечного числа тонких колёс, рассматриваемых только в теории). Эти колёса, по имени изобретателя называемые колёсами Гука, употребляются в механизмах, требующих большой плавности движения. При помощи именно колёс Гука знаменитый мастер Бреге устроил, для определения по мысли Араго и Физо скорости света в жидкостях, снаряд, в котором маленькое зеркальце делало до 2000 оборотов в секунду.

Применение зубчатых колес при различных взаимных положениях их осей

Цилиндрические (лобовые) колеса употребляются для передачи вращения между осями параллельными. Для передачи вращения между осями пересекающимися употребляются конические колеса, а для передачи между осями непараллельными и непересекающимися служат гиперболоидные колеса. Винт, способный вращаться около своей оси, но не имеющий поступательного движения, может быть помещен так, чтобы составлять с зубчатым колесом зацепляющуюся пару. При таком соединении на один оборот винта, называемого иногда червяком, колесо поворачивается на один свой шаг.

[править] Передаточное отношение

Если имеется ряд валов с насаженными на них наглухо последовательно зацепляющимися зубчатыми колесами, по одному колесу на каждом валу, то абсолютная величина отношения угловой скорости первого и последнего вала, сколько бы ни было промежуточных колес, будет та же самая, как если бы первое и последнее колесо зацеплялись между собой непосредственно. Если же желают изменить это отношение, как это требуется, например, при устройстве часов, то на 1-й вал насаживают колесо, сцепляющееся с маленьким колесом, называемым шестерней, насаженным на втором валу, на котором параллельно с шестерней насаживается колесо, сцепляющееся с шестерней 3-го вала, и так далее; наконец, колесо предпоследнего вала сцепляют с шестерней последнего вала. В таком механизме отношение угловых скоростей первого и последнего валов выражается формулой:

ω 1/ ω n = (-1)n-1(m1 m2 m3…mn)/(M1 M2 M3…Mn-1)

где ω 1 — угловая скорость первого вала, ω n — угловая скорость последнего вала, n — число валов, M1M2M3…— число зубцов колес, m1m2m3…— число зубцов шестерен. Множитель (-1) n-1 стоит для того, чтобы показать, что при четном числе валов первый и последний вращаются в противоположные стороны, а при нечетном числе валов — в одну и ту же сторону. Если некоторые из валов в системе зубчатых колес подвижны, то такая система называется эпициклической. Эпициклические системы представляют чрезвычайно богатый материал для преобразования вращения. Так, например, при помощи такой системы, состоящей только из четырёх колес почти одинакового размера, можно достигнуть такой передачи, при которой на 10000 оборотов некоторой части механизма другая его часть делает только один оборот.

Особый, весьма богатый класс составляют механизмы, состоящие из зубчатого колеса с острыми зубцами, круто скошенными в одну сторону и отлого в другую, и задерживающей собачки. Такие колеса называются храповыми. К этому классу относится, между прочим, соединение храпового колеса с якорем маятника в стенных часах и разные другие спуски.

Избыточные связи

Значение Кс зависит от точности изготовления и числа сателлитов.

Структурным анализом* планетарной передачи можно по¬казать, что она является механизмом с избыточными связями. Избыточных связей нет в передаче с одним сателлитом. Но у такой передачи больше нагрузки на зубья, а следовательно, и габариты. Размещение нескольких дополнительных сателлитов приводит к образованию избыточных связей. В механиз¬мах с избыточными связями любые отклонения размеров, например шага зубьев, радиусов расположения осей сателлитов и др., сопровождаются неравномерным распределением нагрузки, в данном случае между сателлитами. Избыточные связи можно устранить, если выполнить одно из центральных колес (чаще колесо а) самоустанавливающимся, т. е. без радиальных опор. Для этих целей применяют соединение колеса с валом по типу зубчатой муфты (см. рис. 17.7). При отсутствии компенсирующих устройств Кс =1,2...2. В передачах с самоустанавливающимся колесом и тремя сателлитами

Кс= 1,1...1,2. (8.81)

Для планетарных передач, выполненных по другим схемам, силы в зацеплении определяют по такому же принципу.

При известных окружных силах нетрудно определить вра¬щающие моменты на основных звеньях передачи, как произг ведениях этих сил на соответствующие радиусы. Для определенния моментов и сил в общем виде Τβ § γ используют структурную схему планетарной передачи как трехзвенного механизма (рис. 8.47).

По условию равновесия,

По условию сохранения энергии,

В этих уравнениях моментам и их произведениям на угловые скорости приписывают знак плюс при совпадении направлений Τ и Ъ (ведущие звенья) и знак минус, если они противоположны (ведомые звенья). Кроме того, в формуле (8.83) пока не учтены потери на трение.

Два уравнения позволяют определить два неизвестных момента при одном заданном и известных ω. Например, при ведущем а и закрепленном b (соь = 0) с учетом к. п. д. η ah из уравнения (8.83) найдем

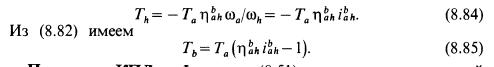
Пассивные звенья

Такие звенья дублируют друг друга и вводятся для повышения жесткости конструкции. Пассивной связью можно назвать дополнительное звено, которое не накладывает ограничений на движение механизма. Обычно она вводится для увеличения жёсткости механизма или перевода механизма через особые положения, в которых наблюдается неопределенность движения звеньев.

В так называемом “механизме параллельных кривошипов” (рис. 7, а) звено 3 может изменить направление вращения при неизменном направлении вращения ведущего звена 1, когда механизм приходит в горизонтальное положение. Для того, чтобы этого избежать, в состав механизма включают дополнительное звено 4.

При структурном анализе механизма пассивные связи не учитывают. Если по формуле степень подвижности механизма будет равна нулю, но заранее известно, что рассматриваемая цепь подвижна, то следует искать пассивные

Динамика машин и механизмов

Динамика машин и механизмов

        раздел теории машин и механизмов, в котором изучается движение механизмов и машин с учётом действующих на них сил. Д. м. и м. решает следующие основные задачи: установление законов движения звеньев механизмов, регулирование движения звеньев, нахождение потерь на трение, определение реакций в кинематических парах, уравновешивание машин и механизмов.

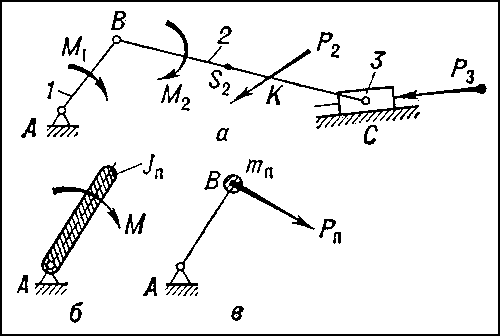
         Определение законов движения звеньев механизма по заданным характеристикам внешних сил решают с помощью дифференциальных уравнений движения механической системы или машинного агрегата, состоящего обычно из двигателя, передаточного механизма, рабочей машины и иногда управляющего устройства. Число уравнений равняется числу степеней свободы этой механической системы. В плоских механизмах с одной степенью свободы для удобства решения задачи все силы и массы приводят к одному звену или точке механизма, которые называются звеном приведения или точкой приведения. Условный момент, приложенный к звену приведения, называется моментом приведения. Момент приведения равен совокупности всех моментов и сил, приложенных к звеньям механизма. Условный момент инерции звена приведения называется приведённым моментом инерции. Кинетическая энергия звена приведения равна сумме кинетических энергий всех звеньев механизма. Аналогично определяют приведённые силу и массу в точке приведения (рис., а):

        

        где М_п — приведённый момент; J_п — приведённый момент инерции; Р_п — приведённая сила; m_п — приведённая масса; M₁, M₂, P₂, P₃ — моменты и силы, приложенные к звеньям механизма; ω₁, ω₂ — угловые скорости звеньев; υ_B, υ_C — скорости точек В и С механизма; υS₂ — скорость центра тяжести звена 2; υ_K — скорость точки К приложения силы P₂; α₂ — угол между векторами P₂ и υ_K; α₃ — угол между векторами P₃ и υ_C. Уравнение движения для данного случая:

        

        т. е, М_п в общем случае зависит от времени, положения, скорости.

         Уравнения движения обычно являются нелинейными. Методов точного решения их не существует, поэтому пользуются приближёнными графическими, графо-аналитическими и численными методами интегрирования. Установить закон движения механической системы сложнее, если учитывать трение и зазоры в кинематических парах, упругость и переменность масс звеньев. Иногда, например при изучении быстротекущих процессов в машинах, некоторые внешние силы нельзя считать заданными, т.к. движение механизма может оказать обратное воздействие на характеристику этих сил. Например, в некоторых режимах с большими ускорениями нельзя принимать механическую характеристику электродвигателя как заданную зависимость момента на валу двигателя от угловой скорости, т.к. на этот момент существенное влияние могут оказать электромагнитные процессы в электродвигателе. В этом случае к дифференциальным уравнениям движения механической системы добавляют дифференциальное уравнение электромагнитных процессов в электродвигателе и решают их совместно.

         Вопросы регулирования движения машинного агрегата и управления им рассматриваются в теории регулирования. Различают неустановившийся, переходный и установившийся режимы движения. При установившемся режиме скорости точек механизма являются периодическими функциями времени или положения или остаются постоянными. Регулирование установившегося движения сводится к обеспечению угловой скорости звена приведения, не превышающей допустимого отклонения от её значения. Для этого рассчитывают и устанавливают на машину специальную массу — Маховик. Необходимость регулирования неустановившегося движения возникает в том случае, когда, несмотря на непериодическое изменение внешних сил или масс, в механизме требуется поддерживать среднюю скорость звена приведения постоянной. Для этого на машину устанавливают специальные автоматические регуляторы. Основной задачей при этом является определение устойчивости движения системы машина — регулятор. Если же скорость какого-либо звена (или др. параметра) нужно изменять по заданному закону (программе), то в машину встраивают программное устройство. Примером может служить программное управление металлорежущими станками. Конкретная задача, рассматриваемая теорией регулирования, — отыскание оптимальных режимов движения машин (оптимальное управление). Например, определение движения с наибыстрейшим переходным режимом при ограниченном ускорении, т. е. оптимального по быстродействию, или движения с минимумом затрачиваемой в переходном режиме энергии, т. е. оптимального по потерям.

         Нахождение непроизводительных потерь в машинах сводится к определению потерь на трение, которые являются основными и влияют на эффективность работы машин и механизмов. Степень использования энергии в машине оценивается механическим кпд.

         Кинетостатический расчёт механизмов, выполняемый при известном законе движения механизма, производится определением реакций в кинематических парах от всех заданных внешних сил, а также сил инерции звеньев и сил трения в кинематических парах. Значения этих реакций входят в расчёты звеньев на прочность и необходимы для подбора подшипников и расчёта их смазки.

         Уравновешивание машин и механизмов осуществляется рациональным подбором и размещением Противовесов, снижающих динамические давления в кинематических парах механизмов. На практике осуществляют уравновешиванием машины на фундаменте (предотвращение вибраций) или уравновешиванием вращающихся масс — балансировкой. Инерционные силы в современных быстроходных машинах достигают больших значений. Переменные по величине и направлению силы инерции нарушают нормальную работу узлов машины, являются источником вибраций и шума, которые вредно воздействуют на обслуживающий персонал и нарушают нормальную работу др. механизмов и приборов. В вибрационных машинах рассчитывают условия создания интенсивных колебаний их исполнительных органов. Динамические исследования в машинах непосредственно связаны с расчётами на прочность и жёсткость элементов машин, которые проводятся с целью выбора размеров и конструктивных форм деталей. Методы таких расчётов обычно излагаются в учебных дисциплинах: сопротивление материалов, динамика сооружений, детали машин.

         Динамические исследования проводят также для пространственных механизмов со многими степенями свободы. Системы подобного типа обладают большой универсальностью выполняемых операций.

        

        

        Действие сил и моментов кривошипно-ползунного механизма (а) в звене приведения (б) и в точке приведения (в): 1 — кривошип; 2 — шатун: 3 — ползун; М — приведённый момент М_П; А — неподвижная опора.

Все силы, действующие в механизмах, условно подразделяются на:

• внешние, действующие на исследуемую систему со стороны внешних систем и совершающие работу над системой. Эти силы в свою очередь подразделяются на:

  • движущие, работа которых положительна (увеличивает энергию системы);

  • сопротивления, работа которых отрицательна (уменьшает энергию системы). Силы сопротивления делятся на:

    • силы полезного (технологического) сопротивления - возникающие при выполнении механической системы ее основных функций (выполнение требуемой работы по изменению координат, формы или свойств изделия и т.п.);

    • силы трения (диссипативные) - возникающие в месте связи в КП и определяемые условиями физико-механического взаимодействия между звеньями (работа всегда отрицательна);

  • взаимодействия с потенциальными полями (позиционные) - возникают при размещении объекта в потенциальном поле, величина зависит от потенциала точки, в которой размещается тело (работа при перемещении из точки с низким потенциалом в точку с более высоким - положительна; за цикл, т.е. при возврате в исходное положение, работа равна нулю). Потенциальное поле - силы тяжести или веса. Существуют электромагнитные, электростатические и другие поля.

• внутренние, действующие между звеньями механической системы. Работа этих сил не изменяет энергии системы. В механических системах эти силы называются реакциями в КП.

• расчетные (теоретические) - силы, которые не существуют в реальности, а только используются в различных расчетах с целью их упрощения:

  • силы инерции - предложены Д’Аламбером для силового расчета подвижных механических систем. При добавлении этих сил к внешним силам, действующим на систему, устанавливается квазистатическое равновесие системы и ее можно рассчитывать, используя уравнения статики (метод кинетостатики).

  • приведенные (обобщенные) силы - силы. совершающие работу по обобщенной координате равную работе соответствующей реальной силы на эквивалентном перемещении точки ее приложения.

Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта КП нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил.

Уравнение движения механизма

Для определения законов движения начальных звеньев за заданными силами используются уравнения, которые называются уравнениями движения механизма. Число этих уравнений равняется числу степеней подвижной механизма.

Уравнения движения механизма могут быть представлены в разных формах. Для механизмов с одной степенью вольности одна из самых простых форм уравнений получается на основе теоремы об изменении кинетической энергии : изменение кинетической энергии механизма на некотором перемещении равняется сумме работ всех сил, которые действуют на звенья механизма на этом самом перемещении. Данный закон подают в виде уравнения

(4.9)

где Т — кинетическая энергия механизма в произвольном положении; Т0 — кинетическая энергия механизма в положении, которое принимается за начальное; _ — сумма алгебраизма работ всех сил и моментов, которые прилагаются к механизму на некотором перемещении.

Работу осуществляют все активные силы и моменты и силы трения во всех кинематических парах механизма.

Уравнение движения в энергетической форме. Сведем все силы и моменты механизма с одной степенью вольности к одному звену возведения, то есть заменим рассматриваемый механизм его динамической моделью. Поскольку вся нагрузка, прилагаемая к модели, выражается возведенным моментом МЗВ, то правая часть уравнения (4.9) равняется

(4.10)

а именно уравнение (4.9), учитывая, можно записать в виде

. (4.11)

Уравнение (4.11) называют уравнением движения механизма в энергетическом виде, или — в форме уравнения кинетической энергии. В целом верхний предел _ интегрирования в (4.11) считается переменной.

Динамический анализ и синтез механизмов.

В отличие от кинематики, в динамике механизмов и машин изучается движение звеньев в зависимости от сил, действующих на кинематические пары и звенья механизма, вызывающих это движение. Различают две задачи: определение действующих на машину сил и определение закона движения машины. Анализ действующих сил необходим для определения мощности, необходимой для движения механизма, расчета на прочность и износостойкость отдельных его деталей, выбора рациональных размеров звеньев и их формы. Все внешние силы и пары сил, которые могут действовать на звенья механизма или машины разделяют на несколько групп. Силы движущие . Эти силы приложены к ведущим звеньям и предназначены для преодоления сопротивлений машины. Считают, что при работе механизма они совершают положительную работу. К числу движущих сил можно отнести давление газов на поршень двигателя внутреннего сгорания; момент, развиваемый электродвигателем, и др. Силы сопротивления. Это силы, для преодоления которых создается машина или механизм. Их подразделяют на силы "полезного" и "вредного" сопротивления. Силы "полезных" сопротивлений приложены к ведомым звеньям машины и направлены так, что препятствуют их движению. На преодоление этих сил затрачивается полезная работа машины. "Вредными" называются сопротивления, вызывающие непроизводительную затрату энергии движущих сил. Это силы, действующие в кинематических парах, - силы трения, удара и др., а также силы сопротивления среды. Силы тяжести G. Равнодействующие сил тяжести машины и ее звеньев имеют постоянные модули и приложены в центрах их тяжести. В зависимости от направления перемещения центров тяжести эти силы совершают или положительную работу (перемещение вниз), или отрицательную (перемещение вверх) работу. Силы инерции. Силы инерции и мометы сил инерции возникают при переменном движении звеньев механизма. Это силы воздействия ускоряемого тела на тела, вызывающие его ускорение. В общем случае элементарные силы инерции звена могут быть сведены к главному вектору сил инерции, приложенному в центре масс, и главному моменту этих сил:

где m - масса звена; - ускорение центра масс звена; - момент инерции звена относительно оси, проходящей через центр масс и перпендикулярной к плоскости движения; - угловое ускорение звена. Реактивные силы. В кинематических парах возникают силы взаимодействия звеньев - реакции. В их обозначениях первая цифра в индексе указывает, со стороны какого звена действует сила, а вторая - номер звена, на которое она действует т.е. силы равны по модулю, но имеют противоположные направления. Основную задачу силового расчета механизма можно сформулировать следующим образом. Даны: а) кинематическая схема и основные размеры всех звеньев механизма;

б) закон движения ведущего звена;

в) массы и моменты инерции звеньев;

г) внешние силы, действующие на звенья;

д) силы инерции. Требуется определить силы, действующие в кинематических парах, уравновешивающую силу или момент на каком-либо звене механизма, закон движения которого известен. Рассмотрим зубчатый механизм (рис. 3.9).

Рис. 3.9

Рациональные передаточные отношения Так как

то передаточное отношение механизма

. Условие соосности: Условие сборки: , где К - число сателлитов. Числа зубьев колес подбирают путем совместного решения уравнений передаточного отношения и условия соосности с учетом условия сборки. При заданных статические моменты М и мощности N на ведущих валах механизма определяем с учетом следующих зависимостей.

Cилы, действующие на звенья механизма, можно определить, рассматривая условия равновесия каждого звена (рис. 3.10). Определим приближенно (без учета к.п.д.) силы, действующие на звенья механизма.

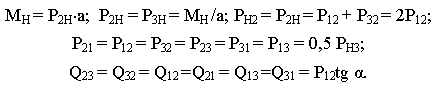
Эти силы учитывают при расчете колес, валов и подшипников механизма.

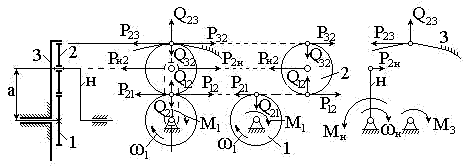
Рис. 3.10