2.2. Способы задания графов

Выше мы познакомились с двумя способами описания графов: графическим, и в виде двух множеств вершин V и ребер Е, когда каждое ребро е Е определено парой инцидентных ему концевых вершин (v', v "). Рассмотрим другие способы, используемые в теории графов.

В общем, виде задать граф - значит, описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать. Пусть v₁, v₂,..., v_j ... ,v_n - вершины графа G: е₁, е₂,... , е_j,..., е_т – ребра. Отношение инцидентности задается:

1) матрицей инцидентности || || размера тхn: по вер­тикали и горизонтали указываются вершины и ребра соот­ветственно, а на пересечении i-й вершины и j-го ребра в случае неориентированного графа проставляется 1, если они инцидентны, и 0 — в противном случае, т.е.

=

а в случае орграфа: -1, если вершина является началом ребра, 1 - если вершина является концом ребра, и 0 - если вершина и ребро не инцидентны; если некоторая вершина яв­ляется для ребра и началом, и концом (т.е. ребро - петля), проставляется любое другое число, например 2, т.е.

2) скам ребер графа, представленным двумя столбца­ми: в левом перечисляются все ребра е_i Е, а в правом -инцидентные ему вершины для н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;

3) атрицей смежности || || - квадратной матрицей размера пхп: по вертикали и горизонтали перечисляются все вершины , а на пересечении k-й и l-й вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины; для орграфа равно числу ре­бер с началом в k-й вершине и концом в l-й.

Если два графа равны, то их матрицы совпадают. Если в графе поменять нумерацию вершин, матрицы (и список ребер) в общем случае изменяются, т.е. вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Строго говоря, граф считается полностью заданным, если нумера­ция его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, являются изоморфными. Проверка изоморфности графов - в общем случае трудоемкая задача.

Пример 1. Задать матрицами инцидентности и смежности, а также списком ребер графы G₁, G₃ (см. рисунок 2.6).

Матрицы инцидентности графов G₁ и G₃ приведены на рисунке 2.7. В матрице инцидентности в каждом столбце только два элемента, отличных от 0 (или один, если ребро - петля).

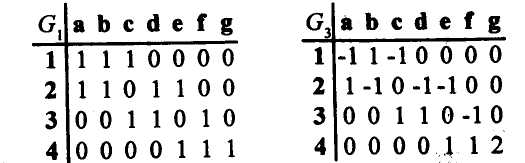
Рисунок 2.7

Список ребер является более компактным описанием графа. Список ребер орграфа G₃ приведен на рисунке 2.8, для н-графа G₁ он аналогичен, однако последовательность указания вершин здесь безразлична.

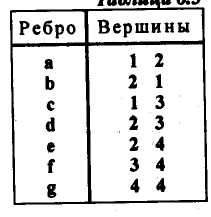
Рисунок 2.8

Матрицы смежности графов даны на рисунке 2.9.

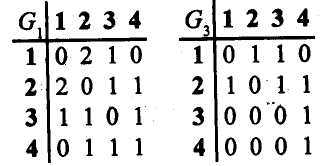
Рисунок 2.9

2.4. Сети и их свойства1

(Кудрявцева А. Группа ПС-285)

Иногда возникает необходимость рассматривать графы, ребрам которых поставлено в соответствие некоторое число.

Ориентированный граф N = (V,D,a) где V – множество вершин графа, D – множество дуг графа, а a - функция из множества вершин графа в множество неотрицательных действительных чисел называется сетью.

Если е – дуга графа, то число a(е) в зависимости от контекста называется либо длиной, либо весом, либо пропускной способностью дуги. При изображении сети a(е) проставляется рядом с дугой е.

Для сетей можно обобщить понятие полустепени исхода и полустепени захода вершины. Пусть N = (V,D,a) – сеть, v – вершина этой сети. Полустепенью исхода v) вершины v называется сумма a(е) по всем дугам, исходящим из v, полустепенью захода v) вершины v – сумма a(е) по всем дугам, заходящим в v. Для сетей, так же как и для орграфов справедливо утверждение о том, что сумма полустепеней исхода и сумма полустепеней захода всех вершин совпадают.

Как и в случае орграфов, вершина сети v, для которой v)>0 и v)=0 называется источником, а вершина , для которой )>0 и )=0 – стоком.

Пути в сетях

Путь – это последовательность дуг, такая, что конец одной дуги является началом другой дуги.

Длиной пути называется сумма длин дуг, составляющих путь.

Длина кратчайшего (u,v)–пути называется расстоянием d(u,v) от вершины u до вершины v. Если (u,v)–пути не существует, то d(u,v)= . Расстояние от u до u равно нулю.

Для сети N возникает задача нахождения расстояния d(u,v) для данных вершин u и v и соответствующего кратчайшего пути.

Задача о кратчайшем пути (ЗКП) между фиксированными вершинами формулируется следующим образом: в заданной сети N с двумя выделенными вершинами v₀ и v найти кратчайший (v₀,v)-путь.

Алгоритм Форда-Беллмана ⁽²⁾

Данный алгоритм был предложен независимо Ричардом Беллманом (1958) и Лестером Фордом (1956).

Будем считать, что количество вершин n сети количества ребер m сети и в сети нет контуров отрицательной длины.

Первый этап – вычисление расстояний от v₀ до всех остальных вершин.

Основная идея алгоритма Форда-Беллмана заключается в поэтапном вычислении кратчайших расстояний. Обозначим через d_k(v) длину кратчайшего среди всех (v₀,v) путей, содержащих не более чем k дуг. Тогда будут справедливы следующие неравенства:

.

Т.к. по предположению в графе нет контуров отрицательной длины, кратчайший (v,v₀)-путь не может содержать более чем n-1 дуг. Поэтому величина дает искомое расстояние от v₀ до v.

Для вычисления d_n-1(v) достаточно последовательно вычислять d_k(v) для всех k=1,…,n-1.

Значения d₁(v) вычисляются просто:

d₁(v) = d(v₀,v) для всех v V.

Пусть значения d_k-1(v) вычислены для всех v V. Легко видеть, что

d_k-1(v) = min{d_k(v), d_k( )+d( ,v)| V}.

Организовать все эти вычисления можно с помощью всего лишь одномерного массива D длины n.Положив D[v] = d(v₀,v) для всех вершин v V, будем иметь равенства

D[v] = d₁(v).

Просматривая после этого вершины v, произведем пересчет значений D[v] по формуле

D[v] = min{D[v], D[ ] + d( ,v)| V}.

После завершения первого пересчета значений D[v] для всех v, будем иметь неравенства D[v] d₂(v). Повторив n-2 раза процесс пересчета D[v], будем иметь равенства D[v] = d_n-1(v), т.е. D[v] дает расстояние от v₀ до v.

Еще один алгоритм - алгоритм Дейкстры, названный в честь известного скандинавского специалиста по компьютерным наукам Дейкстры. Этот алгоритм вычисляет расстояние от фиксированной вершины v₀ до всех остальных вершин сети и находит кратчайший путь более эффективно, чем алгоритм Форда-Беллмана. Алгоритм заключается в последовательном вычислении расстояний сначала до ближайшей к v₀ вершине, затем до следующей ближайшей и т.д. ⁽¹⁾

Прежде, чем привести описание алгоритма, введем необходимые обозначения. Пусть N=(V,D,a) – сеть, v₀ – фиксированная вершина этой сети, v₁,…,v_k – остальные вершины. Для i=1,…,k расстояние d(v₀,v_i) обозначим через d(v_i). На множестве вершин введем двухместную функцию a(v,v’) следующим образом:

Описание алгоритма, кроме того, еще использует подмножество S множества вершин V.

Алгоритм Дейкстры.

Шаг 1. Полагаем S=V\{v₀}, d(v_i)=a(v₀,v_i) для всех i=1,…,k.

Шаг 2. Если S=1, то выполнить шаг 4, иначе выбрать в S элемент v’, для которого величина d(v’) является наименьшей (среди всех элементов из S).

Шаг 3. Положить S=S\{v’}, d(v)=min{d(v), d(v’)+a(v’,v)} для всех vS и перейти к шагу 2.

Шаг 4. Выдать d(v₁),…,d(v_k). Конец работы алгоритма.

Алгоритм осуществляет «итеративный» процесс нахождения расстояния d(v_i) для i=1,…,k. Проследим, как это делается для сети N, изображенной на рис.1. Работа алгоритма будет иллюстрироваться заполнением таблицы 1.

При выполнении первого шага алгоритма величины d(v_i) примут значения, которые указаны в нулевой строке таблицы. Из них точным является только d(v₂), значения остальных величин завышены. На шаге 2 в качестве v’ выбирается вершина v₂ (в таблице соответствующее значение набрано жирным шрифтом) и удаляется из S на шаге 3. На том же шаге уточняются предыдущие значения d(v) для v S (см. первую строку таблицы 1). На этом первый проход алгоритма заканчивается. На втором проходе в качестве v’ берется v₅, удаляется из S и значения d(v) для v S снова уточняются. Результат уточнения отражен во второй строке таблицы. Когда множество S будет содержать только вершину

Рис. 1

Таблица 1

Номер строки	d(v1)	d(v2)	d(v3)	d(v4)	d(v5)
0	4	1
1	3	-		5	3
2	3	-		4	-
3	-	-	4	4	-
4	-	-	4	-	-

V₃ алгоритм заканчивает работу. Результат: d(v₁)=3, d(v₂)=1, d(v₃)=4, d(v₄)=4, d(v₅)=3.

Поскольку на каждом проходе алгоритма число элементов множества S уменьшается на единицу, то алгоритм Дейкстры всегда заканчивает работу.

Случай бесконтурной сети ⁽²⁾

В этом случае, так же как и в случае сетей с неотрицательными весами дуг, известен более эффективный алгоритм вычисления расстояний от фиксированной вершины до всех остальных, чем алгоритм Форда-Беллмана. В основе этого алгоритма лежат две леммы.

Лемма 1. В каждом бесконтурном орграфе имеется хотя бы одна вершина, полустепень исхода которой равна нулю.

Лемма 2. Вершины бесконтурного ориентированного графа можно перенумеровать так, что каждая дуга идет из вершины с меньшим номером в вершину с большим номером.

Орграфы с так пронумерованными вершинами иногда называют топологически отсортированными, а алгоритм, осуществляющий такую нумерацию вершин – алгоритмом топологической сортировки вершин.

При описании алгоритма вычисления расстояний в бесконтурной сети будем считать, что все вершины заданной сети топологически отсортированы. Расстояние будем вычислять от вершины v₀.

Пусть v_k – произвольная вершина заданной бесконтурной сети. Тогда любой (v₀,v_k)-путь проходит через вершины с меньшими чем k номерами. Из этого замечания следует, что для вычисления расстояний от v₀ до всех остальных вершин сети достаточно последовательно вычислить расстояния от v₀ до v₁, затем от v₀ до v₂ и так далее. Пусть, как и раньше, d(v) обозначает расстояние от v₀ до v. Тогда d(v₀) = 0, и если d(v_r) для всех r < k вычислено, то

d(v_k) = min{d(v_r) + d(v_r,v_k)| r = 1,2,…,k}.

Задача о максимальном пути

Задача о максимальном пути формулируется следующим образом: в заданной сети N = (V,D,a) с выделенной вершиной v₀ для каждой вершины v V найти (v₀,v)-путь, имеющий максимальную длину среди всех возможных (v₀,v)-путей в сети N.

Отметим, что имеет смысл решать эту задачу лишь в сетях, не содержащих контуров положительной длины. Рассмотрев тогда сеть, отличающуюся от исходной только изменением знаков весов дуг, получим сеть, в которой нет контуров отрицательной длины. Применяя к новой сети алгоритм Форда-Беллмана, можно построить кратчайшие (v₀,v)-пути, которые будут путями максимальной длины в исходной сети.

Потоки в сетях ⁽³⁾

Если мы припишем каждой дуге ориентированного графа поток некоторого вещества, граф становится удобной моделью при исследовании целого ряда проблем в транспорте, связи и других областях, связанных с действительным или воображаемым движением товаров, информации или людей.

Для данной сети N = (V,D,a) определим поток через N как функцию , сопоставляющую каждой дуге a из D неотрицательное действительное число (называемое потоком через a) таким образом, что для любой дуги a; по отношению к сети N полустепень исхода и полустепень захода любой вершины (отличной от v и ) равны между собой. Рассуждая неформально, это означает, что поток через любую дугу не превосходит ее пропускной способности и что "полный поток", входящий в любую вершину (отличную от v и ), равен "полному потоку", выходящему из нее. Другим потоком является нулевой поток, при котором поток через каждую дугу равен нулю (любой другой поток называется ненулевым).

Дуга a, для которой , называется насыщенной; остальные дуги называются ненасыщенными.

Направление потока определяется знаком (а).

Вершины сети N обычно классифицируются по их воздействию на поток (создают, поглощают или сохраняют поток). Чтобы формализовать классификацию, обозначим через v V множество дуг, для которых v является начальной вершиной, а через V v—множество дуг, для которых v является конечной вершиной. Тогда целое число Q(v, ), определяемое соотношением

называется чистым потоком из v относительно .

Сеть в целом сохраняет любой поток в том смысле, что . Это хорошо видно из следующего выражения:

т.к. каждая дуга сети входит точно один раз в каждую двойную сумму.

Отношения между потоками и операции над ними

Пусть и — потоки в одной и той же сети N=(V, D), и пусть р — целое число. Тогда для каждой

дуги а D потоки , и определяются с помощью следующих соотношений:

( ) (а)= (а) + (а),

( ) (а)= (а) - (а),

(а)= (а).

Легко видеть, что

Q(v, )=Q(v, ) Q(v, ),

Q(v, )= Q(v, ).

Будем писать < тогда и только тогда, когда (а)< (а) для каждой а D. Отношения между потоками , > и определяются аналогично. Говорят, что поток ограничен значениями и , если величина (а) заключена между (a) и (а) для каждой дуги сети. Очевидно, что достаточным условием ограниченности потока потоками и является выполнение одного из следующих соотношений: или . Вообще, по некоторым дугам поток может быть ограничен сверху потоком а по другим — потоком .

Потоки и называются согласованными, если (а)* (а) 0 для каждой дуги а V. Другими словами, и согласованы, если не существует дуг а, для которых (а) и (а) отличны от нуля и противоположно направлены. Потоки { , ..., } в одной и той же сети называются совместно согласованными, если они попарно согласованы.

Связь понятий согласованных и ограниченных потоков устанавливается теоремой:

Теорема: Если S={ , ,.. ., }—множество совместно согласованных потоков в сети N, — произвольный поток в N и T S, то поток ограничен потоками и .

Простые потоки

Пусть в данной сети N = (V,D,a) есть множество дуг, образующих простую цепь пли простой цикл в соответствующем неориентированном графе. Предположим, что мы ориентируем ребра, проходя эти простые цепи и циклы в одном из возможных направлений. Дуга С будет называться нормальной, если ее вновь введенная ориентация совпадает с исходной и обращенной (инвертированной) в противном случае.

Потоки с ограничениями на дугах

Сеть N = (V, D) называется сетью с ограниченной пропускной способностью, если на D определены две функции и , принимающие целочисленные значения, удовлетворяющие соотношению 0 (а) (a) для всех а D, Целые числа (а) и (а) называются верхней и нижней границами пропускной способности дуги а и интерпретируются как максимально и минимально допустимая величина потока по каждой дуге. Если (а)=0 для всех а D, то (a) обычно называется пропускной способностью дуги а, а сеть называется транспортной сетью. Поток в сети называется допустимым тогда и только тогда, когда (а) (а) (а) для всех а D.

Если и — допустимые потоки, а —любой поток, ограниченный потоками и , то очевидно, что также является допустимым.

Максимальные потоки

Сумма потоков через дуги, инцидентные v, равна сумме потоков через дуги, инцидентные w; эта сумма называется величиной потока. Будем в первую очередь интересоваться потоками, имеющими наибольшую возможную величину, — так называемыми максимальными потоками. В общем случае сеть может иметь несколько различных максимальных потоков, однако их величины должны совпадать.⁽⁴⁾

Изучение максимальных потоков через сеть N = (V,D,a) тесно связано с понятием разреза, т.е. такого множества A дуг орграфа D, которое обладает тем свойством, что любая простая цепь из v в проходит через дугу, принадлежащую A. Пропускной способностью разреза называется сумма пропускных способностей принадлежащих ему дуг. Разрезы, обладающие наименьшей возможной пропускной способностью, называются минимальными разрезами.

Величина любого потока не превышает пропускной способности любого разреза, и, следовательно, величина любого максимального потока не превышает пропускной способности любого минимального разреза. Однако сразу не ясно, что два последних числа всегда равны между собой; Этот результат был получен американскими математиками Фордом и Фалкерсоном в 1955 году и назван теоремой о максимальном потоке и минимальном разрезе.

Теорема (о максимальном потоке и минимальном разрезе). Во всякой сети величина любого максимального потока равна пропускной способности любого минимального разреза.

Теорема о максимальном потоке и минимальном разрезе позволяет проверять, максимален данный поток или нет, но только для достаточно простых сетей. Разумеется, на практике приходится иметь дело с большими и сложными сетями, и в общем случае трудно найти максимальный поток простым подбором. Опишем один алгоритм нахождения максимального потока в любой сети с целочисленными пропускными способностями.

Шаг 1. Сначала подберем поток , обладающий ненулевой величиной (если такой поток существует). Например, если N – сеть, представленная на рис. 29.3, то подходящим будет поток, изображенный на рис. 29.4. Стоит отметить, что чем больше величина выбранного нами начального потока , тем проще будут последующие шаги.

Шаг 2. Исходя из N, строим новую сеть N’ путем изменения направления потока на противоположное. Более точно, любая дуга a, для которой (a) = 0, остается в N’ со своей первоначальной пропускной способностью, а любая дуга a, для которой , заменяется дугой a с пропускной способностью и противоположно направленной дугой с пропускной способностью (a). Сеть N’ в нашем примере показана на рис. 29.5. Вершина v уже не является источником,а – стоком.

Шаг 3. Если в сети N’ мы сможем найти ненулевой поток из v в , то его можно добавить к первоначальному потоку и получить в N новый поток ’большей величины. Теперь можно повторить шаг 2, используя при построении сети N’ новый поток ’ вместо . Повторяя эту процедуру, мы в конце концов придем к сети N’ , не содержащей ненулевых потоков; тогда соответствующий поток будет максимальным потоком. Например, на рис. 29.5 существует ненулевой поток, в котором потоки через дуги (v,u), (u,z), (z,x), (x,y) и (y, ) равны единице, а потоки через остальные дуги равны нулю. Добавляя этот поток к потоку на рис. 29.4, получим поток, изображенный на рис. 29.6; повторяя шаг 2, легко показать, что это и есть максимальный поток.

Используемая литература:

(1) http://pgap.chat.ru/zap/zap264.htm#0

(2) Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы матроиды, алгоритмы

(3) Басакер Р., Саати Т. Конечные графы и сети.

(4) Уилсон Р. Введение в теорию графов