5.6. Число подмножеств данного множества

Пусть А = {a_l, а₂, ..., а_n,} - некоторое конечное множество, элементы кото­рого перенумерованы. При работе с конечными множествами на вычисли­тельных машинах такие множества часто задают с помощью характеристи­ческих векторов. Пусть А' А – произвольное подмножество множества А. Характеристический вектор v(A') = ( ) для множества А определя­ется с помощью такого соответствия:

Например если , и , то .

Теорема. , где A’,A’’ – некоторые подмножества множества А.

Доказательство.

Пусть и - характеристические векторы множеств А' и А" соответственно. Если А' = А", то для всякого i имеем . Отсюда следу­ет, что . Наоборот, если , то для всякого i имеем . По определению характеристического вектора, если , то принадлежит как множеству , так и множеству , а если , то элемент не принадлежит ни тому ни другому подмножеству. Отсюда следует, что подмножества А' и А"состоят из одних и тех же элементов, т.е. .

Теорема доказана.

Следствие 1: Число различных подмножеств n-элементного множества равно 2".

Действительно, поскольку число компонент характеристического вектора равно n и каждая компонента может принимать одно из двух значений­ 0 или 1, то число различных возможных характеристических векторов по ос­новному правилу комбинаторики равно 2 * 2 * ... * 2 = 2".

Следствие 2:

Действительно, поскольку – число различных k-элементных подмно­жеств n-элементного множества, то сумма всех таких чисел составляет число всех подмножеств данного n-элементного множества.

5.7. Размещение элементов множества

Пусть дано некоторое неупорядоченное n-элементное множество А. Сколько, разных упорядоченных k-элементных подмножеств может иметь множество А? Рассмотрим два возможных варианта этой задачи:

- подмножества имеют k различных элементов;

- подмножества имеют k не обязательно различных элементов. I

Следовательно, в первом варианте задачи подмножества задаются не избыточно, а во втором, – избыточно, однако число всех различных элементов подмножества вместе с числом всех экземпляров каждого из его элементов равно k. Упорядоченное k-элементное подмножество множества А, все элементы ко­торого различны, называется размещением без повторений, а любое упоря­доченное k-элементное подмножество множества А, все k элементов которого не обязательно различны, называется размещением с повторениями. Заме­тим, что в первом случае , причем если k=n, то В этом случае размеще­ние является перестановкой. Во втором случае k не обязательно должно быть меньше n, т. е. возможно, что .

Решение первого варианта задачи.

Поскольку множество А неупорядочено, то любое его k-элементное под­множество может быть упорядочено одним из k! способов, а число всех возможных различных k-элементных подмножеств множества А равно . Следовательно, число всех возможных размещений из n элементов по k равно k! , т. е. имеет место следующая теорема

Теорема.

Количество упорядоченных k-элементных подмножеств n-элементного множества, все k элементов которого различны, равно

Пример 1:

Студенту необходимо сдать три экзамена на протяжении семи дней. Сколькими способами это можно сделать?

Решение: Искомое число способов равно количеству трехэлемент­ных упорядоченных подмножеств множества из семи элементов, т. е. существует = 7 * 6 * 5 = 210 способов.

Если известно, что последний экзамен будет сдаваться на седьмой день, то число способов равно З * = 3 * 6 * 5 = 90.

Пример 2:

Сколькими разными способами можно разместить пять студентов в ауди­тории, которая имеет 20 мест?

Решение: Искомое число способов равно числу размещений из 20 элементов по 5 элементов, т. е. = 20 * 19 * 18 * 17 * 16 = 1 860 480.

Решение второго варианта задачи.

Пусть B={b₁, b₂,..., b_k} - некоторое конечное k-элементное множество, а А={а₁,а₂,...,а_n}-n-элементное множество и f : - функция из В в А. Как известно, функцию f можно задать с помощью таблицы значений

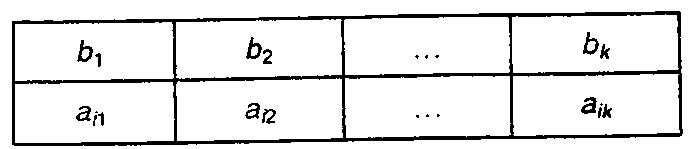
где . Теперь нашу задачу можно сформулировать так: сколько существует функций из множества В в множество А? В такой формулировке задача решается достаточно просто.

Условимся называть кортежем длины k элементы вида (а₁, а₂, ... , a_k), где а; - не обязательно различные элементы некоторого конечного множест­ва А. Поскольку каждый элемент a_ij может быть любым элементом мно­жества А, то число различных кортежей вида (a_i1 ,a_i2 ,...,a_ik) может быть n^k.

Теорема.

Количество различных упорядоченных k-элементных под­множеств n-элементного множества, все k элементов которого не обязательно различны, равно n^k .

Пример:

Сколько различных слов можно составить:

В алфавите из восьми букв.

Решение: Всех таких слов будет столько, сколько существует отображений восьмиэлементного множества в множестве из двух элементов, т.е. по теореме 2⁸=256 слов.

В алфавите из шестнадцати букв.

Решение: В этом алфавите имеем 2¹⁶=65536 слов.