5.4. Перестановки

При составлении размещений без повторений из п по k мы по­лучали расстановки, отличающиеся друг от друга либо составом, либо порядком элементов. Но если брать расстановки, которые включают все п элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называются перестановками из п элементов, а их число обознача­ется Р_n Следовательно, число перестановок равно Р_п = =п!. Перестановки элементов 1,2,..., п записывают и в матричной форме , где верхняя строка - это по­рядковые номера 1, 2,..., п позиций элементов в перестановке; нижняя строка - тот же набор чисел 1, 2,..., п, взятых в каком-ли­бо порядке; - номер элемента на j-м месте перестановки. По­рядок столбцов в перестановках, записанных в матричной форме, не является существенным, так как в этом случае номер позиции каждого элемента в перестановке указывается явно в верхней строке. Например, перестановка (3,2,4,1) из четырех элементов может быть записана как , , и т.д.

Пример:

Сколькими способами можно расположить на шахматной доске 8 ладей, чтобы они «не били» друг друга?

Решение: Условие «не могли бить» означает, что на каждой го­ризонтали и вертикали может стоять лишь одна ладья. Ввиду это­го, каждому расположению ладей на доске соответствует перестановка . Верхняя строка перестановок – это номера горизонталей, нижняя - вертикалей, пересечение которых определяет положение ладей на доске. Следовательно, число рас­становок равно числу перестановок Р₈ = 8! из 8 элементов.

5.5. Число различных k-элементарных подмножеств n-элементарного множества

Посмотрим теперь, сколько существует разных подмножеств из k элементов в множестве, состоящем из п элементов (k < п).

Теорема Число различных k-элементных подмножеств n-элементарного множества равно

,

где сокращение п! = п * (п - 1) * ... * 3 * 2 * 1 называется факториалом числа n (читается n-факториал). Причем 0! = 1. А сокращение .

Доказательство. Чтобы построить k-элементное подмножество множества А, необходимо к (k - 1)-элементному множеству присоединить один из п - k + 1 элементов, которые не входят в это подмножество. Поскольку число (k - 1)­элементных подмножеств равно , И каждое из этих подмножеств можно сделать k-элементным п - k + 1 способами, по основному правилу комбина­торики получаем число * (n - k + 1) подмножеств. Однако не все эти подмножества будут различными, поскольку любое k-элементарное подмножество можно также построить k способами. Следовательно,

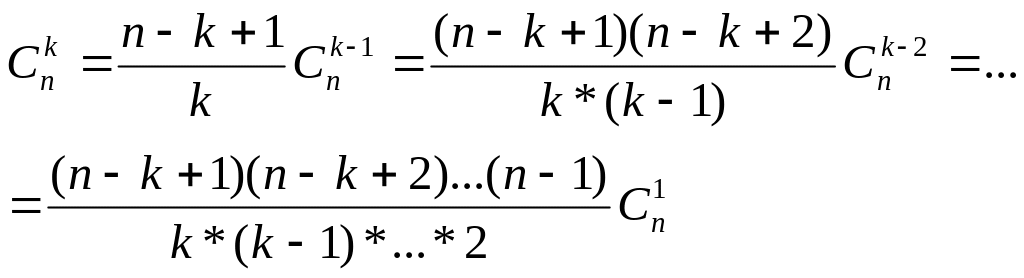
Поскольку – число одноэлементных подмножеств множества А – равно n, то

Теорема доказана.

Произвольное k-элементное подмножество множества А называется комбинацией, или выборкой, а число – числом комбинаций или сочетаний из n элементов по k элементов.

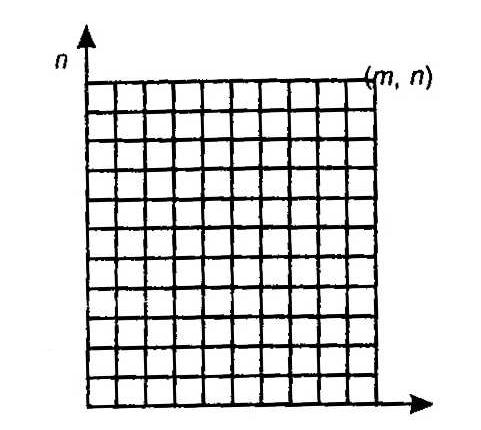
Рис. 5.2.

Биномиальные коэффициенты имеют интересную геометрическую интерпре­тацию. Пусть имеем прямоугольную шахматную доску размером m на n, раз­мещенную на координатной плоскости. Эта доска состоит из m*n элементарных квадратов, разделенных n - 1 горизон­тальной линией и m - 1 вертикальной. Определим, сколькими разными самыми короткими путями можно попасть из точки (0, 0) в точку (m, n) на этой доске.

Каждый самый короткий путь, ведущий из точки (0, 0) в точку (m,n), состоит, очевидно, из m + n сторон элементарных квадратов, среди которых m гори­зонтальных и n вертикальных. Эти пути отличаются между собой только 1 числом вертикальных и горизонтальных сторон. Значит, общее количество путей равно числу способов, какими из т + n сторон можно выбрать n верти­кальных, т.е. это число равно .

Заметим, что можно было бы вести подсчет не по вертикальным сторонам,

а по горизонтальным. То есть, существует различных самых коротких путей и, следовательно, справедливо равенство:

.

Данное равенство имеет название «формула симметрии».

Из этой формулы имеем следствие:

,

имеющее название «формула сложения». Докажем данное следствие.

Доказательство:

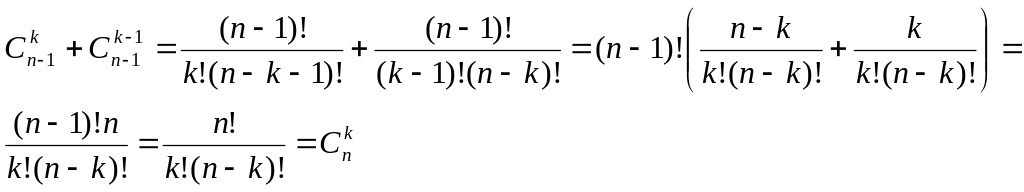
следствие доказано.

Пример:

Сборная команда университета по волейболу насчитывает 15 человек. Сколько разных вариантов должен рассмотреть тренер перед игрой, чтобы заявить список игроков на игру?

Решение: Число игроков волейбольной команды равно шести. Значит, число всех возможных вариантов - это число различных подмножеств, состоящих из шести элементов в множестве из пятнадцати элементов. Следовательно, по теореме 2 имеем

.