5. Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского.

Пусть S – двусторонняя замкнутая поверхность, ограничивающая тело V. Предположим, что функции имеют непрерывные частные производные в V и непрерывны на S. Докажем справедливость формулы Гаусса-Остроградского:

, (ФГО)

где поверхностный интеграл взят по внешней стороне поверхности S.

Доказывать формулу Гаусса-Остроградского будем отдельно для каждого слагаемого в подынтегральном выражении.

Докажем, что .

1. Сначала представим, что поверхность S либо пересекается любой прямой, параллельной оси OZ не более, чем в двух точках, либо отрезок этой прямой принадлежит S.

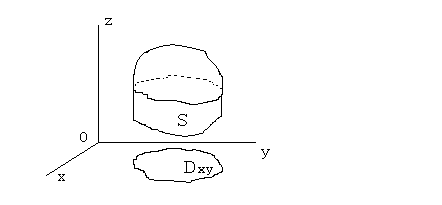
В этом случае поверхность S проецируется на область на плоскости XOY и можно параметризовать S следующим образом: , где . При этом та часть поверхности S, которая содержит отрезки прямых, параллельных оси OZ (обозначим ее ), проецируется на граничные точки . Интеграл по этой части поверхности равен нулю. Учитывая, что поверхностный интеграл взят по внешней стороне поверхности, получим , что дает

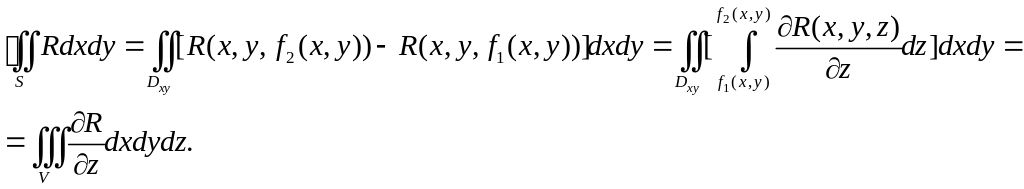
2. Для того, чтобы доказать формулу в общем случае, разобьем тело V поверхностями, параллельными оси OZ, на конечное число тел с граничными поверхностями , удовлетворяющими требованиям предыдущего пункта. Для каждого из полученных тел и соответствующих граничных поверхностей формула Гаусса-Остроградского справедлива. Поскольку интегралы по поверхностям, параллельным оси OZ, равны нулю, получим ,

что и требовалось доказать.

Соотношения и доказываются аналогично. Таким образом, справедливость формулы Гаусса-Остроградского доказана.

Элементы теории поля.

Полем называют скалярную или векторную функцию, заданную в каждой точке некоторой части пространства и являющейся физической характеристикой этой части пространства. В зависимости от вида заданной функции различают скалярное или векторное поле.

Примеры скалярных полей: поле температур, поле электрического потенциала.

Примеры векторных полей: поле скоростей, силовое поле.

Характеристики скалярного поля.

Пусть задано скалярное поле функции , .

Поверхностью уровня данного скалярного поля называется поверхность, задаваемая уравнением .

П р и м е р. Пусть на множестве трехмерного пространства задано поле температур . Очевидно, что . При любом значении множество значений , то есть, , представляет собой сферическую поверхность радиуса . Благодаря поверхностям уровня легко представить, как температура уменьшается при удалении от источника теплового излучения, находящегося в начале координат.

Скалярное поле может задаваться не только в пространстве, но и в области на плоскости.

Примером плоского скалярного поля может служить поле значений высоты над уровнем моря, заданное на карте местности.

Линией уровня плоского скалярного поля называется кривая, находящаяся в области задания скалярной функции и задаваемая уравнением .

П р и м е р. Пусть на множестве плоскости XOY задано поле высот над уровнем моря . Значения функции меняются в диапазоне . При любом значении множество значений

, то есть, представляет собой эллипс, причем чем меньше полуоси эллипса, тем выше точки этого эллипса находятся над уровнем моря. Точка, соответствующая началу координат, находится на наибольшей высоте, равной .

Градиентом скалярного поля , , называется вектор-функция, заданная на , и равная .

С помощью градиента определяют производную функции по направлению. Если – единичный вектор направления, то . Как известно, наибольшее изменение в фиксированной точке функция претерпевает в направлении градиента в этой точке.

По заданной функции легко построить градиент. Обратно, если известен градиент функции, то есть, все ее частные производные, то саму функцию легко восстановить с точностью до постоянного слагаемого по формуле

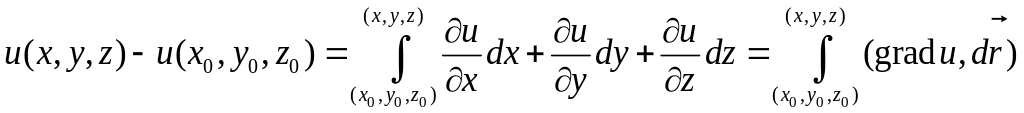
Характеристики векторного поля.

Рассмотрим поле вектора , .

Векторной линией данного векторного поля называется линия, касательная к которой в любой точке параллельна вектору поля, определенному в этой точке. В случае поля скоростей векторные линии называются линиями тока, в случае электростатического поля – силовыми линиями.

Выведем систему дифференциальных уравнений векторных линий. Согласно определению вектор параллелен вектору . Следовательно, справедливы соотношения

, которые и являются дифференциальными уравнениями векторных линий в пространстве.

П р и м е р. Определить векторные линии векторного поля .

Р е ш е н и е. Составим систему дифференциальных уравнений векторных линий:

.

Решая, например, уравнения и , получим систему системы плоскостей и цилиндрических поверхностей при произвольных наборах констант и . Пересечения этих плоскостей и поверхностей – это и есть векторные линии данного векторного поля.

Дивергенцией данного векторного поля с непрерывно дифференцируемыми компонентами является скалярная величина

.

Термин дивергенция (или расхождение) поля в точке связан с наличием дополнительных источников или стоков в этой точке. Для того, чтобы не зависеть от выбранной координатной системы при определении дивергенции, в дополнение к аналитическому дадим механическое определение дивергенции. Пусть точка . Возьмем шар с центром радиуса , лежащий в . Поверхность этого шара обозначим .

Сосчитаем поток вектора поля через поверхность в направлении внешней нормали:

.

Согласно формуле Гаусса-Остроградского . В силу непрерывности дивергенции возможно применение к последнему интегралу теоремы о среднем: , где точка . Таким образом, . Пусть теперь . Тогда вследствие непрерывности дивергенции . Поэтому мы получаем следующее определение дивергенции в точке :

,

где – поток вектора поля через сферу радиуса с центром в точке .

Иногда для определения дивергенции в точке вместо шара берут произвольное тело, содержащее , рассматривают поток через поверхность этого тела, и дивергенцию определяют как отношение потока к объему тела при стягивании тела в точку .

П р и м е р. Найти дивергенцию поля вектора 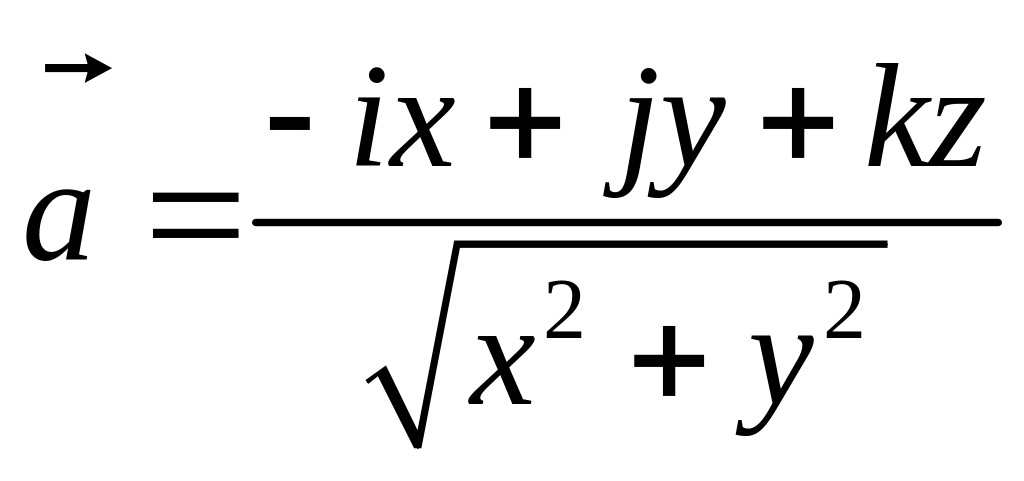в точке (3,4,5).

Циркуляцией вектора , , вдоль некоторой замкнутой ориентированной кривой C , находящейся внутри множества , назовем следующий криволинейный интеграл второго рода:

.

П р и м е р. Найти циркуляцию вектора вдоль лежащих в плоскости XOY окружностей: а) , б) . Обе окружности проходятся так, что круг, ими ограниченный, остается слева.

Р е ш е н и е. Найдем координаты вектора : . В случае а) с учетом параметризации , получим

.

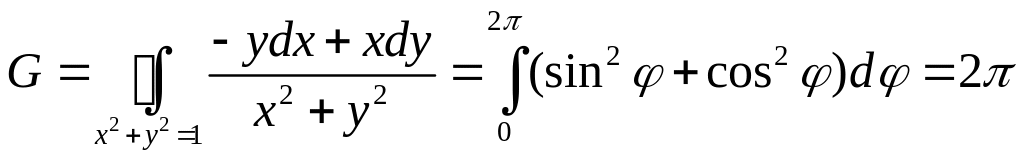В случае б) подынтегральная функция является непрерывно дифференцируемой внутри области, ограниченной заданным контуром, поэтому к ней можно применить формулу Грина. То есть,

.

Ротором вектора поля с непрерывно дифференцируемыми компонентами назовем следующую векторную величину:

.

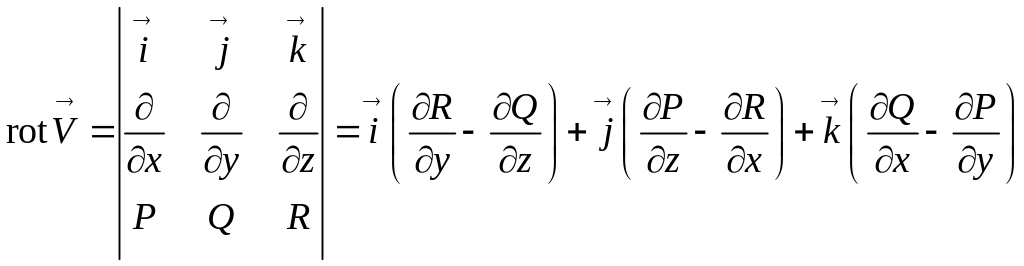Здесь «умножение» элементов второй строки на элементы третьей строки означает, что от функции из третьей строки берется соответствующая производная.

Ротор иногда называют вихрем, он характеризует вращение поля в данной точке. Дадим определение ротора, не связанное с выбранной в координатной системой. Поскольку ротор – векторная величина, а вектор задается своими проекциями на определенные направления, определим проекцию ротора в точке на заданное направление независимо от координат вектора поля. Рассмотрим плоскость с нормалью , содержащую точку . Пусть – лежащая в плоскости окружность радиуса с центром в точке , ориентированная таким образом, что с конца вектора видно, что она обходится в положительном направлении. Найдем циркуляцию вектора поля вдоль окружности :

. В соответствие с формулой Стокса 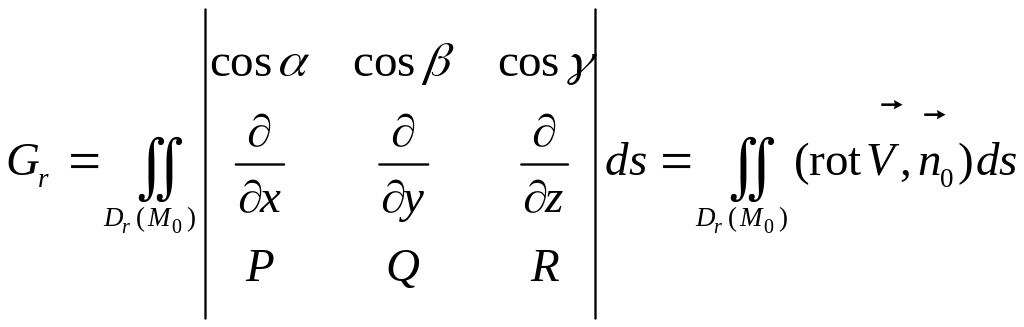, где – круг радиуса с центром в точке , лежащий внутри окружности . Поверхностный интеграл в данном случае представляет собой двойной интеграл по плоской области . Воспользуемся теперь непрерывностью компонент ротора и теоремой о среднем для двойного интеграла. Получим , где точка . Следовательно, . Пусть теперь . Тогда вследствие непрерывности компонент ротора имеем . Следовательно, мы получили проекцию ротора в точке на заданное направление :

,

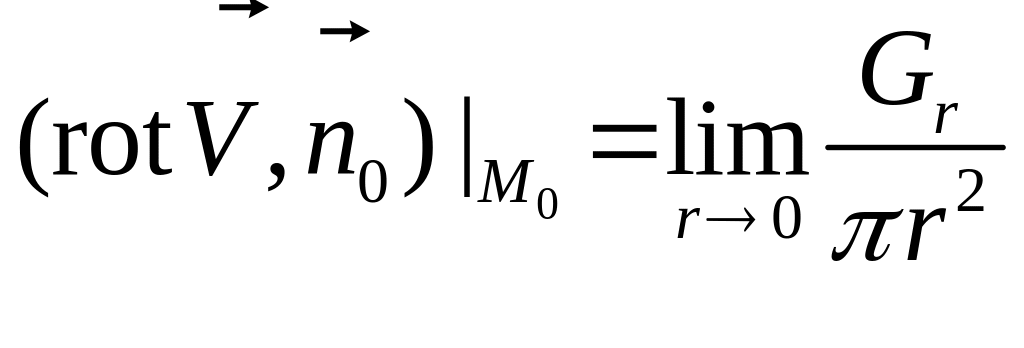где – циркуляция вектора поля по окружности радиуса с центром в точке , лежащей в плоскости с нормалью и ориентированной так, что с конца вектора видно, что она обходится против часовой стрелки.

П р и м е р. Найти ротор вектора .

Оператор Гамильтона (набла-оператор).

Для упрощения записи характеристик скалярных и векторных полей был введен символический векторный оператор, имеющий вид . Символическое «умножение» этого оператора на какую-то величину означает, что каждая из компонент оператора применяется к этой величине.

Например, если – скалярная величина, то .

Для векторных величин возможно как скалярное, так и векторное умножение. Проследим, что дадут такие произведения с оператором в случае векторного поля .

Скалярное произведение: .

Векторное произведение: .

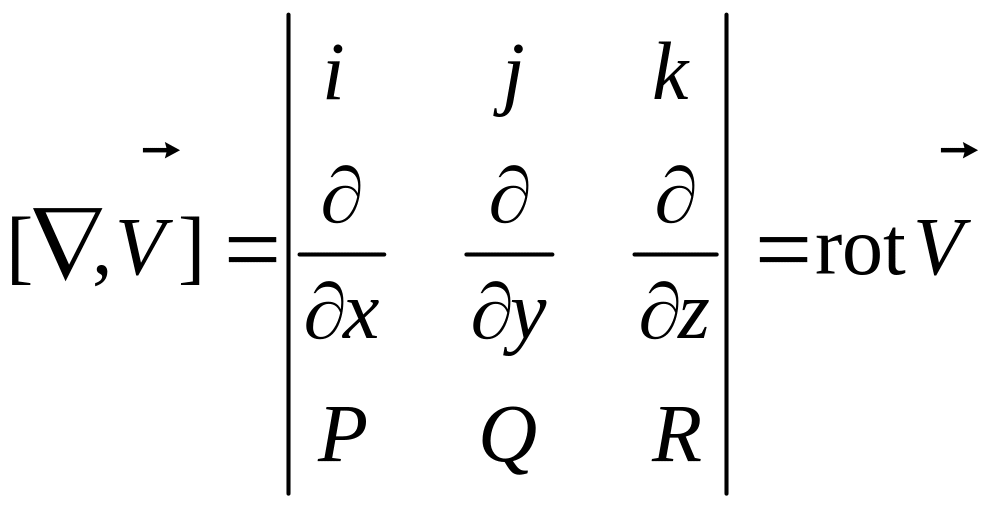Отдельный интерес представляет определенный для скалярных полей оператор

.

Такой оператор называется оператором Лапласа. Функции, удовлетворяющие уравнению Лапласа называются гармоническими в функциями.

Специальные векторные поля.

Потенциальным полем называется поле вектора , , если существует скалярная функция такая, что или . При этом функция называется потенциалом вектора .

У т в е р ж д е н и е. Необходимым и достаточным условием того, что поле вектора потенциально, является выполнение равенства

.

Н е о б х о д и м о с т ь. Пусть поле вектора потенциально, то есть существует функция такая, что . Следовательно, , , . Из определения ротора следует, что все его координаты равны нулю, поэтому .

Д о с т а т о ч н о с т ь. Условие равносильно условию независимости криволинейного интеграла второго рода от пути интегрирования. То есть интеграл с переменным верхним и фиксированным нижним пределом 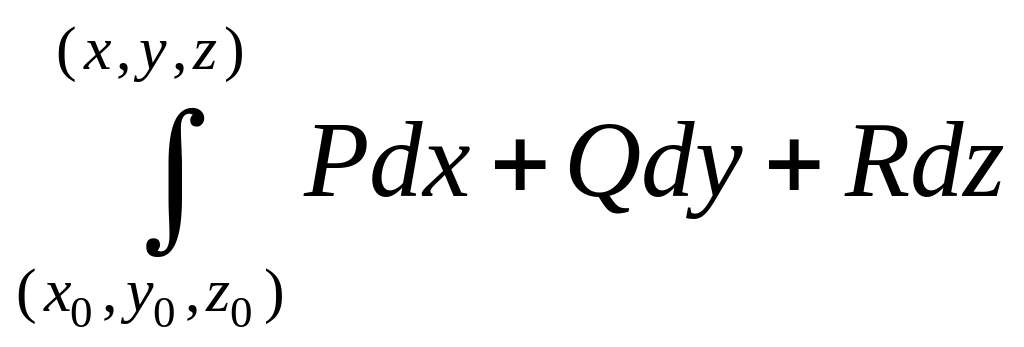является функцией переменных , находящихся в верхнем пределе: . Покажем, что функция является потенциалом вектора . Имеем 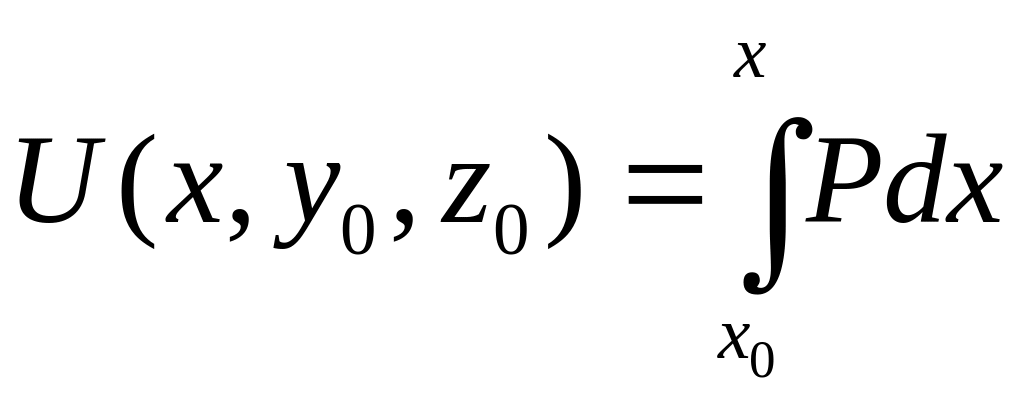, так как интеграл мы взяли по отрезку . Следовательно, . Аналогично доказывается, что .

Таким образом, функция , действительно, является потенциалом вектора .

Итак, потенциальное векторное поле – это безвихревое, бесциркуляционное поле, так как циркуляция вдоль любого замкнутого контура равна нулю.

Пример потенциального поля – поле ньютоновского притяжения.

П р и м е р. Показать, что поле вектора

потенциально, и найти потенциал этого поля.

Соленоидальным полем называется поле вектора , , если существует вектор-функция , , такая, что или , , . В этом случае вектор-функцию называют векторным потенциалом вектора .

У т в е р ж д е н и е. Необходимым и достаточным условием того, что поле вектора соленоидально, является выполнение равенства

.

Н е о б х о д и м о с т ь. Пусть . Тогда

.

Д о с т а т о ч н о с т ь. Пусть . Построим векторный потенциал вектора . Положим для упрощения и построим функции и такие, что и . Можно взять эти функции в ви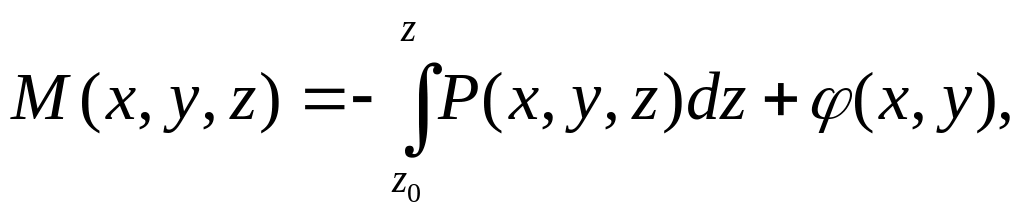де где – неизвестная функция, и 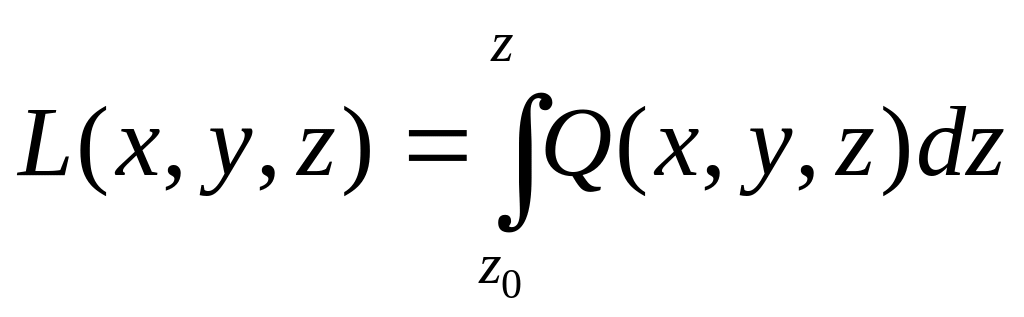. Удовлетворяя равенству и пользуясь тем, что , получим 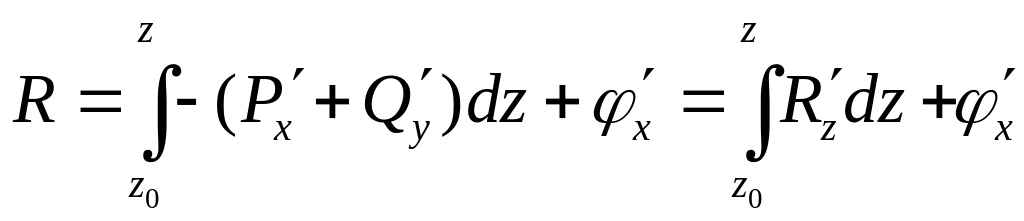. В результате интегрирования по имеем: . Таким образом, неизвестная функция определена: 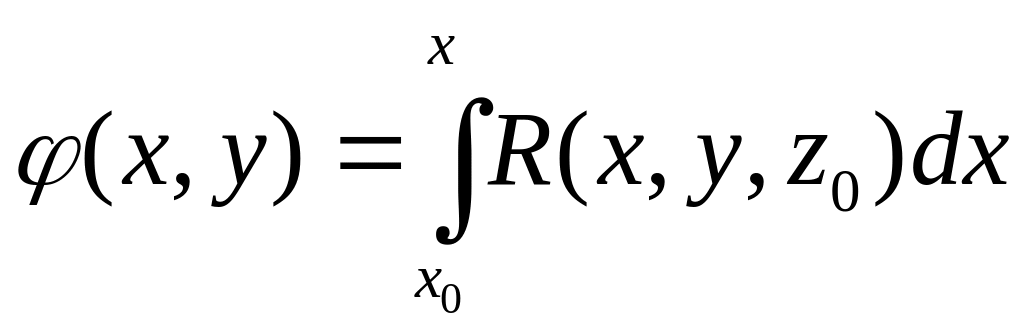. Следовательно, компоненты векторного потенциала построены.

Необходимое и достаточное условие соленоидальности векторного поля на основе формулы Гаусса-Остроградского обеспечивает равенство нулю потока вектора поля через любую замкнутую и ограничивающую некоторое тело поверхность.

Рассмотрим в «векторную трубку». Так называют поверхность, состоящую из векторных линий, в сечении которой поперечником получается замкнутая кривая.

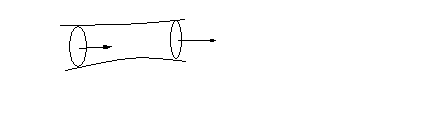
Возьмем замкнутую поверхность, состоящую из векторной трубки и двух поперечников. В соответствии со сказанным выше поток вектора поля через такую замкнутую поверхность равен нулю. Поток через боковую поверхность – векторную трубку – также равен нулю, так как по определению векторных линий направление вектора поля совпадает с направлением векторных линий, и значит, ортогонален к нормали к боковой поверхности. Таким образом, сумма потоков через поперечники внутрь (или вне) замкнутой поверхности равна нулю. Следовательно, в соленоидальном поле поток вектора поля через поперечные сечения векторной трубки сохраняет постоянную величину. Эта величина называется интенсивностью векторной трубки.

П р и м е р. Показать, что поле вектора для любого соленоидально.

Разложение произвольного векторного поля.

Пусть , , – произвольное векторное поле. Покажем, что вектор может быть представлен как сумма двух векторов, один из которых представляет потенциальное, а другой – соленоидальное векторное поле.

Пусть вектор . Какой должна быть эта функция , чтобы вектор был соленоидальным? Поскольку , получим , то есть . Таким образом, чтобы разложить исходный вектор на сумму потенциального и соленоидального векторов, необходимо сначала решить уравнение Пуассона . Такое уравнение всегда имеет решение (и даже бесчисленное множество решений). Определив , мы получим потенциальный вектор . Теперь по построению вектор соленоидальный. Следовательно, требуемое разложение построено.

54