Связь криволинейного интеграла второго рода по замкнутой кривой в пространстве с поверхностным интегралом. Формула Стокса.
Пусть C – гладкая замкнутая пространственная кривая, S – такая двусторонняя поверхность, что кривая C является границей этой поверхности. Тогда справедлива формула Стокса
,
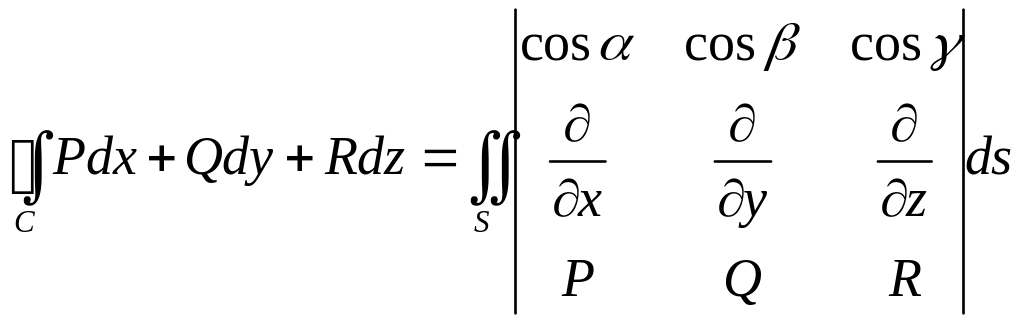(ФС)
где выбор стороны поверхности, а значит, выбор знаков направляющих косинусов нормали к поверхности определяется заданием обхода по кривой C следующим образом: если глядеть с конца вектора нормали к поверхности C, должно быть видно, что обход кривой C совершается против часовой стрелки.
Следует пояснить, что собой представляет правая часть формулы Стокса. Под интегралом находится определитель, в верхней строке которого расположены направляющие косинусы вектора нормали к поверхности S, в средней строке расположены символические операторы нахождения частных производных, и в нижней строке расположены функции, представленные в криволинейном интеграле. Раскладывая определитель по верхней строке, мы получим поверхностный интеграл второго рода. Формальное «умножение» символического оператора на функцию означает, что от этой функции следует взять частную производную по соответствующей переменной.
Приведем другое представление правой части формулы Стокса в виде поверхностного интеграла второго рода по координатам:
.
Нетрудно заметить, что в том случае, когда кривая C расположена в плоскости XOY, и в качестве S мы выберем плоскую область, ограниченную кривой C, формула Стокса превращается в уже известную формулу Грина.
Для доказательства параметризуем поверхность S:
,
.
Будем считать функции
дважды непрерывно дифференцируемыми
в области значений параметров
.
Таким образом, благодаря параметризации
мы перешли от поверхности S
к области
,
находящейся в параметрической плоскости.
Граница C
поверхности S
соответствует границе области
,
которую мы назовем
.
Посчитаем первое слагаемое в криволинейном
интеграле с применением введенной
параметризации и формулы Грина для
интеграла по замкнутой кривой
в параметрической плоскости.
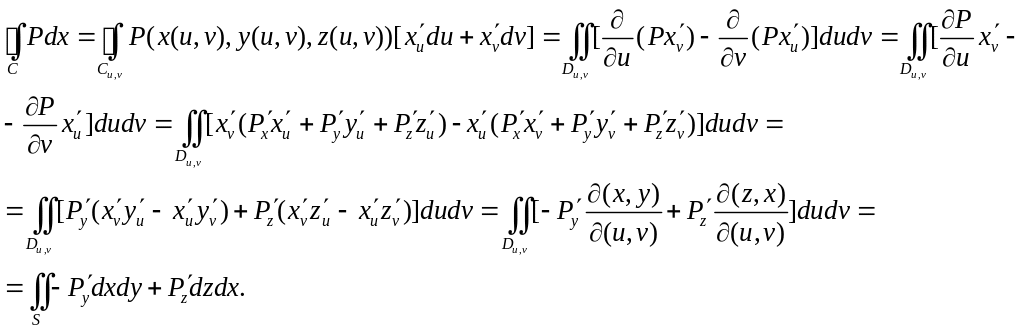
Аналогично
доказывается, что
и
.
Сложив все левые и все правые части полученных соотношений, мы получим формулу Стокса.
Условие независимости криволинейного интеграла второго рода от пути интегрирования в пространстве.
Мы уже нашли необходимое и достаточное условие того, что интеграл второго рода по кривой, расположенной на плоскости XOY и соединяющей две точки, не зависит от формы этой кривой. Получим подобные условия для криволинейного интеграла второго рода по пространственной кривой в случае, когда функции и их первые производные непрерывны. Как и в случае плоской кривой, легко заметить, что условие независимости интеграла по кривой, соединяющей две точки, от формы кривой равносильно условию равенства нулю интеграла по любой замкнутой кривой.
Очевидно, что
условия
,
справедливые в некоторой части
пространства, являются достаточными
для того, чтобы соотношение
выполнялось для любой замкнутой кривой
C,
расположенной в этой части пространства.
Для доказательства следует построить
двустороннюю поверхность с границей
C,
расположенную в этой части пространства,
и применить формулу Стокса.
Докажем, что
эти же условия необходимо выполняются
в той части пространства, где интеграл
по любой замкнутой кривой C
равен нулю. Предположим противное.
Пусть, например,
в некоторой точке M.
В силу непрерывности частных производных
знак
сохраняется в некоторой окрестности
точки M.
Проведем через точку M
плоскость, параллельную плоскости YOZ,
и на этой плоскости в той окрестности
M,
где сохраняется знак выражения
,
проведем замкнутую кривую
.
Имеем
.
Теперь воспользуемся формулой Стокса,
выбрав в качестве поверхности с границей
часть проведенной плоскости, параллельной
YOZ.
Получим
.
Это противоречит предположению о том,
что
.
Таким образом, доказано, что выполнение равенств
в некоторой части
пространства XYZ
равносильно тому, что в этой части
пространства криволинейный интеграл
не зависит от пути интегрирования, а
зависит только от выбора начальной и
конечной точек интегрирования.
Зафиксируем
начальную точку интегрирования
и рассмотрим функцию
,
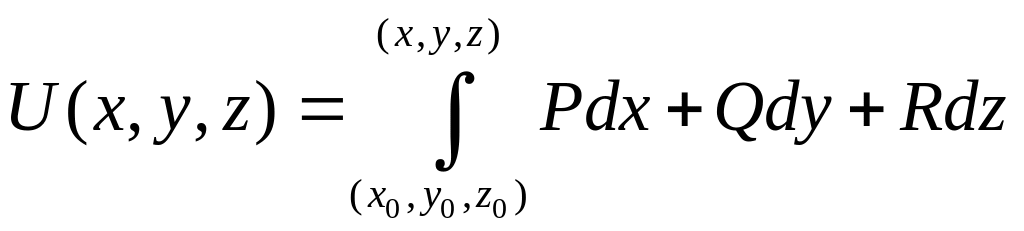где криволинейный интеграл берется по
любому пути, лежащему в
и соединяющему точку
с точкой
.
Рассмотрим
и выберем путь интегрирования вдоль
отрезка прямой
.
Тогда
,
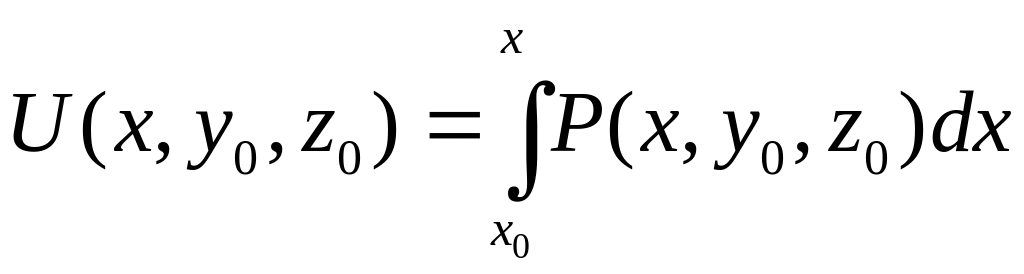и следовательно,
или
.
Аналогично,
и
.
Таким образом,
,
и подынтегральное выражение
является полным дифференциалом функции
,
которая называется потенциалом для
вектор-функции
.