2. Тройные интегралы.

Кубируемые тела.

В теории тройного интегрирования по телу в пространстве большую роль играет понятие объема тела. Простейшим телом, имеющим объем, является прямоугольный параллелепипед, объем которого равен произведению длин трех взаимно ортогональных сторон. Кроме того, в разделе «Двойные интегралы» был определен объем цилиндроида, выпуклого в направлении оси OZ. Кубируемым телом будем называть такое тело, которое разрезами вдоль конечного числа цилиндрических поверхностей с образующими, параллельными осям координат (в том числе, разрезами вдоль плоскостей) может быть разбито на конечное число прямоугольных параллелепипедов со сторонами, параллельными координатным плоскостям и цилиндроидов, выпуклых в направлении координатных осей. В настоящем разделе рассматриваются только кубируемые тела и их кубируемые фрагменты.

Задача о вычислении массы неоднородного тела.

Рассмотрим тяжелое материальное неоднородное тело в пространстве XYZ. Плотностью вещества, из которого состоит тело, назовем , где – объем кубируемого фрагмента, содержащего точку с координатами , – масса этого фрагмента, – диаметр фрагмента. Вследствие неоднородности плотность зависит от местоположения точки, то есть является функцией координат . Будем предполагать, что , – непрерывная функция.

Разделим область на кубируемых фрагментов. Пусть - один из этих фрагментов. Выберем внутри этого фрагмента точку Обозначим через массу вещества внутри , через – объем . В силу непрерывности плотности при достаточно малом диаметре фрагмента можно считать, что Это выполним для всех частей, на которые мы разбили тело. Складывая полученные произведения, найдем массу тела с объемом :

Точное значение массы найдем, если справа перейдем к пределу, когда число разбиений стремится к бесконечности, а все частичные области стягиваются в точку, то есть наибольший из диаметров фрагментов, называемый диаметром разбиения, стремится к нулю:

Определение тройного интеграла.

Пусть в точках тела в пространстве XYZ задана функция Тело разобьем на кубируемых частей с объемами Внутри -ой части с объемом возьмем произвольную точку , в ней вычислим значение заданной функции то есть найдем Это значение умножим на объем Это проделаем со всеми частями, на которые мы разбили область и образуем сумму

Эта сумма называется интегральной суммой для функции по телу . Диаметром фрагмента назовем наибольшее расстояние между двумя точками фрагмента. Диаметром разбиения назовем . Если существует предел интегральной суммы, когда стремится к бесконечности, а диаметр разбиения стремится к нулю, то функцию называют интегрируемой по телу (или по объему) , а сам предел называется тройным интегралом от функции по телу и обозначается

Итак, по определению

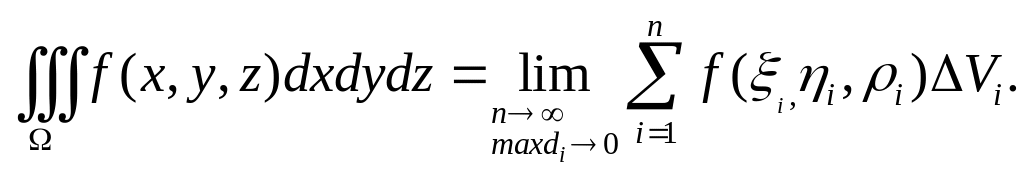
Очевидно, что в случае получим , где – объем тела .

Любая непрерывная функция интегрируема по кубируемому телу . Существуют функции, не являющиеся непрерывными в , но также интегрируемые по , например, функции, имеющие разрыв первого рода на части границы кубируемого фрагмента тела .

Свойства тройного интеграла.

Тройной интеграл обладает свойствами, аналогичными свойствам

двойного интеграла.

1. Тройной интеграл от суммы конечного числа функций равен сумме тройных интегралов от слагаемых функций

.

2. Постоянный множитель можно вынести за знак интеграла

.

3. Если , то

.

4. Если M и m есть соответственно наибольшее и наименьшее значения функции то

.

5. Если функция непрерывна, тело замкнуто, то в найдется по крайней мере одна точка , для которой справедливо равенство

,

где – объем тела (теорема о среднем).

6. Если тело разбито на два кубируемых фрагмента и , то

.

Вычисление тройного интеграла.

Как и в случае двойного интеграла, вычисление тройного интеграла по кубируемому телу сводится к вычислению повторного интеграла.

Рассмотрим сначала случай, когда тело представляет собой цилиндр, в основании которого лежит квадрируемая область , с граничными образующими, параллельными оси OZ и высотой . Проекцией на ось OZ является отрезок . Пусть – непрерывная в точках , и следовательно, интегрируемая по функция. Это значит, что предел интегральных сумм не зависит от способа разбиения тела и от выбора точек внутри фрагментов разбиения. Разобьем область на квадрируемые подобласти с площадями . Разобьем отрезок на равных частей. Проводя цилиндрические поверхности с образующими, параллельными оси OZ и направляющими – границами подобластей и проводя плоскости мы разобьем тело на кубируемых цилиндров , являющихся фрагментами тела . Выберем точки и выберем точки . Очевидно, что Диаметр полученного разбиения тела равен 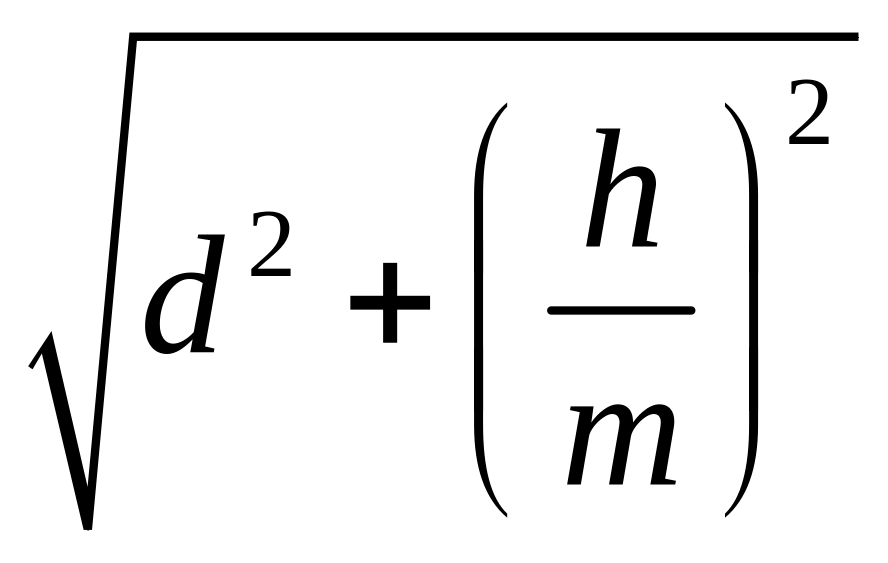, где – диаметр разбиения области на подобласти . Составим интегральную сумму

.

Согласно условию интегрируемости существует предел этой интегральной суммы при . Рассмотрим в правой части последнего равенства сумму, стоящую внутри, по параметру . При фиксированной точке внутренняя сумма представляет собой интегральную сумму для функции по отрезку . Перейдем к пределу при не одновременно, а последовательно: сначала в то время, пока фиксировано. При этом внешняя сумма становится интегральной суммой для непрерывной функции по области . Затем мы перейдем к пределу для внешней суммы. В результате мы получим

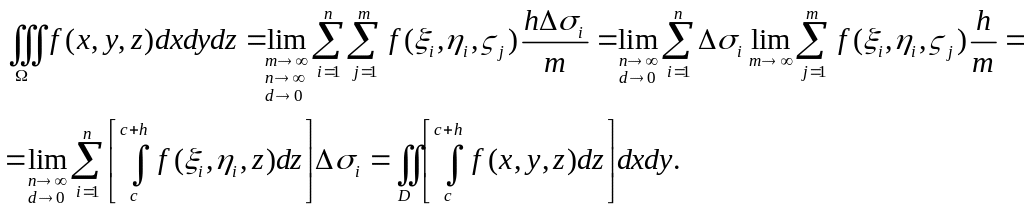
Таким образом, тройной интеграл приведен к повторному: внешнему двойному интегралу по области и внутреннему – по отрезку . В свою очередь, внешний двойной интеграл также сводится вычислению повторного интеграла.

Полученная формула справедлива и в случае, когда интегрируема по телу и, рассматриваемая как функция переменной , имеет конечное число разрывов первого рода на отрезке .

Мы рассмотрели частный случай, когда тело представляет собой цилиндр. Пусть теперь тело выпукло в направлении оси OZ и проецируется на область в плоскости XOY. Пусть уравнения нижней и верхней граничных поверхностей тела и соответственно. Найдем . Определим в проецирующемся на отрезок цилиндре с основанием функцию следующим образом: , если , в остальных точках .

Применяя для функции полученную формулу сведения тройного интеграла к повторному, получим

Опишем вычисление тройного интеграла в случае, когда – выпуклое в направлении осей OY и OZ тело.

Пусть уравнения поверхностей, ограничивающих тело снизу и сверху (в направлении движения по оси OZ) соответственно, и . Пусть уравнения кривых, ограничивающих область снизу и сверху (в направлении движения вдоль оси OY) и . Тогда .

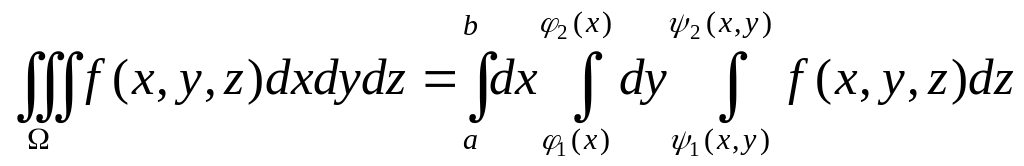Сначала вычисляем внутренний интеграл от функции по , считая и постоянными Используем формулу Ньютона –Лейбница, подставляя вместо верхнего предела , а нижнего . В результате имеем функцию, зависящую только от и . Далее от полученной функции берем интеграл по , считая постоянной. Используем формулу Ньютона-Лейбница, взяв в качестве верхнего предела и нижнего . В результате получаем функцию, зависящую только от . Подсчитав от нее интеграл по отрезку , получим число равное искомому тройному интегралу.

Аналогично сводится к повторному интегрированию тройной интеграл для тела , выпуклого в направлении двух любых координатных осей. В случае, когда тело не обладает таким свойством, разрежем его на фрагменты, выпуклые в направлении двух координатных осей, по плоскостям или цилиндрическим поверхностям с образующими, параллельными осям координат. Последнее возможно вследствие кубируемости .

П р и м е р ы.

1. Вычислить 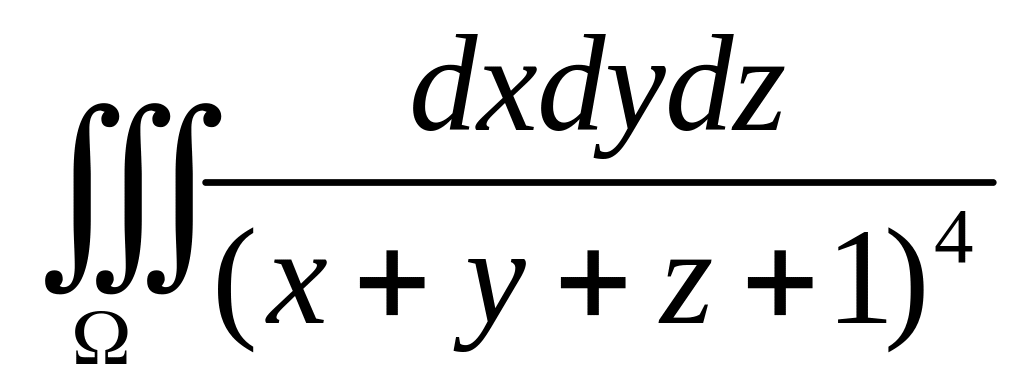, где - тело, ограниченное плоскостями: .

Р е ш е н и е. Проекцией тела на плоскость является область , ограниченная прямыми .

Тогда

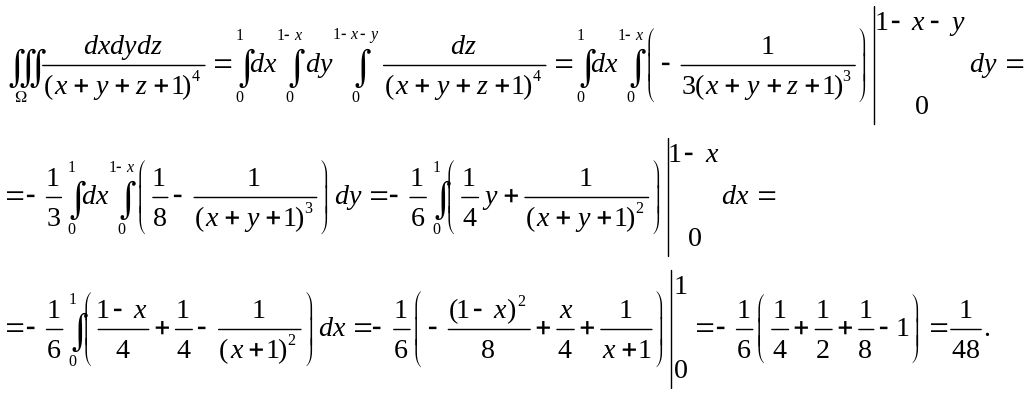
2. Вычислить 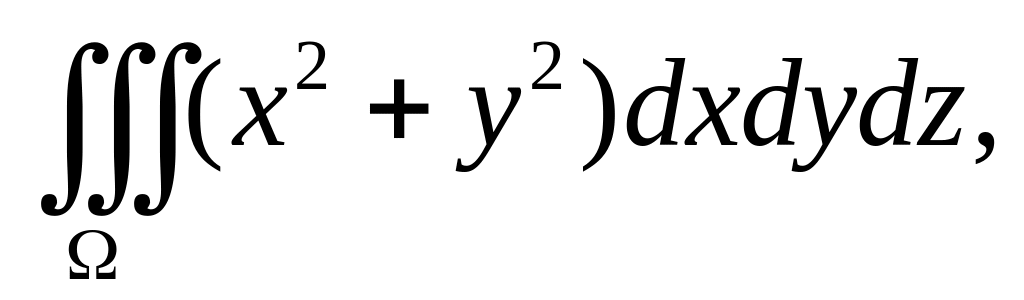где - тело, ограниченное снизу параболоидом вращения 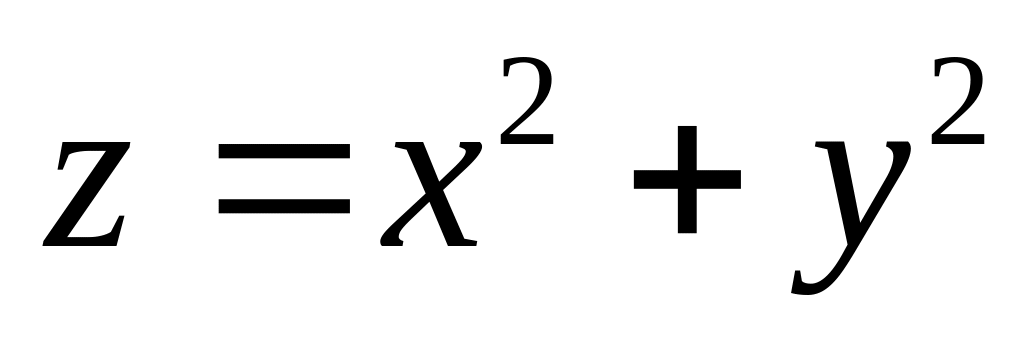, а сверху плоскостью .

Р е ш е н и е. Проекцией тела на плоскость XOY является круг , который и является областью интегрирования . Таким образом,

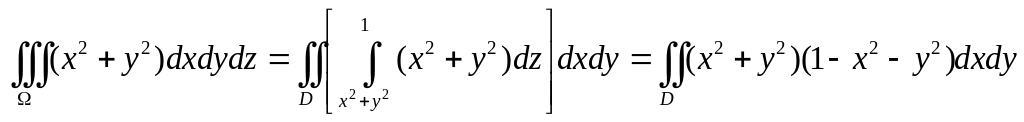. Для упрощения вычисления двойного интеграла перейдем к полярным координатам: . Тогда уравнение границы области примет вид . В результате имеем

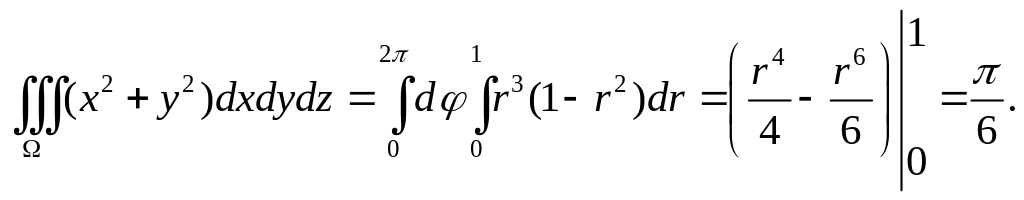
3. Вычислить интеграл где тело ограничено поверхностями .

Замена переменных в тройном интеграле.

Как и в случае двойного интеграла, при вычислении тройного интеграла иногда удобно производить замену переменных. Пусть 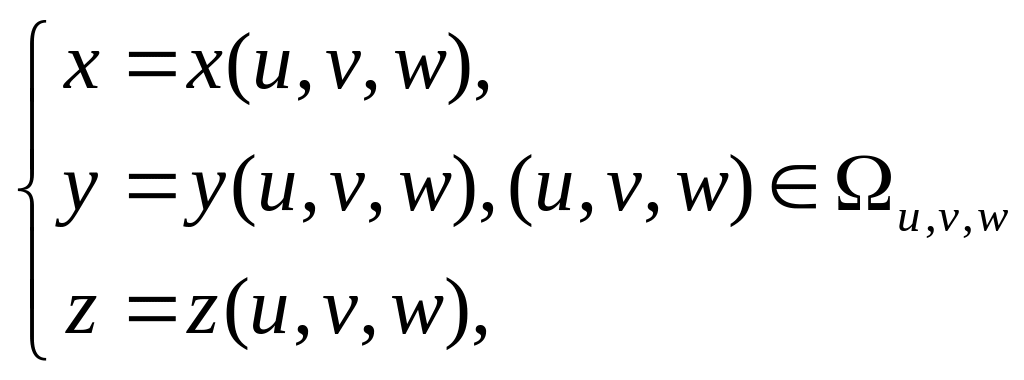, где – прямоугольный параллелепипед со сторонами, параллельными координатным осям в пространстве UVW. Будем предполагать, что функции , и имеют непрерывные частные производные первого порядка в , то есть, отображение непрерывно дифференцируемо, причем .

Возьмем малый прямоугольный параллелепипед в с вершинами , , , , , , , . При отображении , вершины переходят в точки с координатами

, , , , , , .

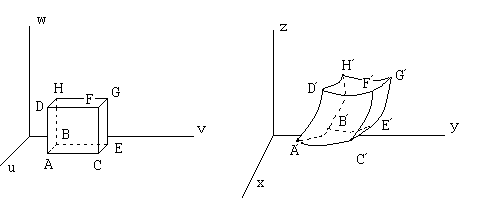
Если малы, то вследствие непрерывной дифференцируемости отображения образы сторон прямоугольного параллелепипеда мало отличаются от прямых, а тело близко к параллелепипеду, построенному на векторах , , , координаты которых представляют собой приращения функций в точке по каждому из аргументов, и потому выражены через эти приращения аргументов по формуле Лейбница:

,

,

где .

Объем такого параллелепипеда равен модулю смешанного произведения векторов , , , и вследствие непрерывности производных, может быть представлен в виде

,

где при .

Пусть теперь прямоугольный параллелепипед в плоскости UVW разбит плоскостями, параллельными координатным плоскостям, на малых прямоугольных параллелепипедов . При этом тело в пространстве XYZ разобьется на фрагменты близкие к параллелепипедам.

Подсчитаем сумму объемов этих фрагментов то есть объем тела . В соответствии с полученной выше формулой объем равен

,

где – вершины прямоугольных параллелепипедов , и , если диаметр разбиения стремится к нулю. Поскольку , где – объем прямоугольного параллелепипеда , мы можем получить точное значение , измельчая разбиения и переходя к пределу в предыдущем выражении для .

Заметим, что первое слагаемое в этом выражении является интегральной суммой для непрерывной в функции , а второе стремится к нулю при измельчении разбиений. Таким образом,

, где .

Построим теперь интегральную сумму для произвольной интегрируемой по функции для уже рассмотренного разбиения тела на прямоугольные параллелепипеды . При этом, согласно полученной формуле для объема тела в пространстве XYZ, объем каждого фрагмента равен , где .

Выберем в каждом фрагменте точку . Это возможно, так как вследствие интегрируемости функции мы можем выбирать произвольную точку внутри фрагмента . В результате интегральная сумма для получения интеграла равна

,

и представляет собой интегральную сумму для функции по прямоугольному параллелепипеду . Очевидно, что диаметры разбиений и одновременно стремятся к нулю в силу непрерывности отображения . Поэтому

.

П р и м е р ы.

1. Вычислить , где тело ограничено конусом и плоскостью .

Р е ш е н и е. Если использовать для вычисления декартовы координаты, то появятся радикалы, которые затруднят вычисление. Поэтому введем цилиндрические координаты:

, .

Пределы изменения параметров обусловлены тем, что уравнение конической поверхности в новых координатах имеет вид , и в пересечении конуса с плоскостью получим окружность , а в цилиндрических координатах . Модуль якобиана преобразования равен

.

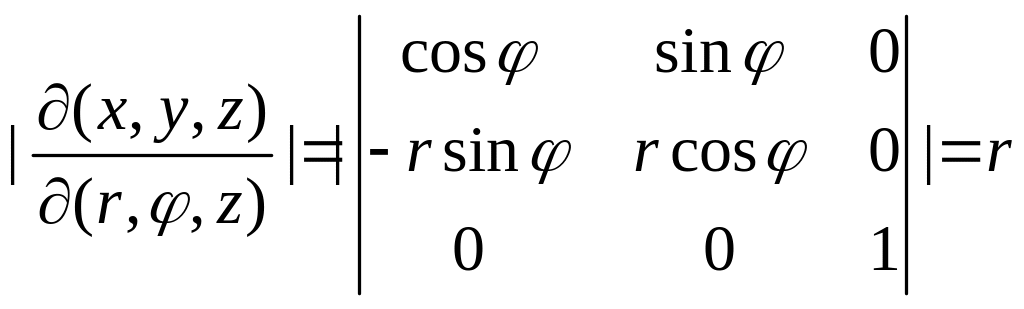Таким образом, .

2. Вычислить интеграл , где тело ограничено эллипсоидом

.

Р е ш е н и е. В целях упрощения счета введем обобщенные сферические координаты, что позволит избежать радикалов в подынтегральных функциях:

,

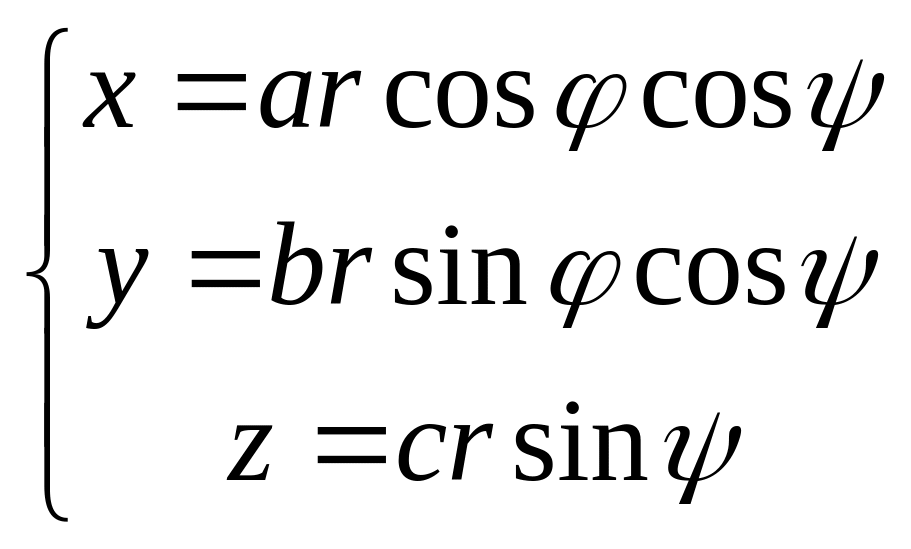так как в обобщенных сферических координатах уравнение поверхности, ограничивающей тело, будет . Вычислим модуль якобиана преобразования:

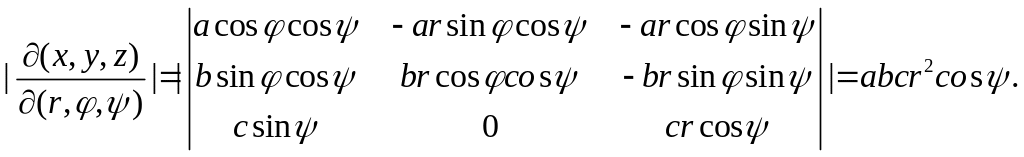
Итак, .

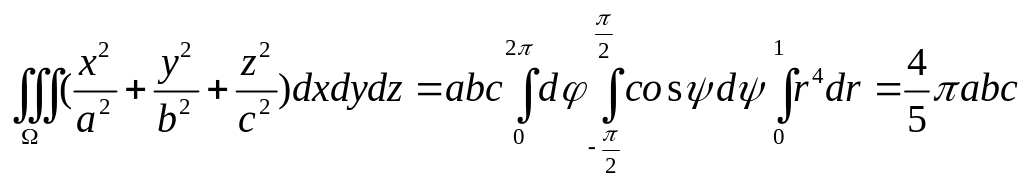3. Вычислить , где тело расположено в октанте

и ограничено поверхностями .

Криволинейные интегралы