Кратные интегралы
Двойные интегралы.
Квадрируемые плоские области.
В теории двойного
интегрирования по области на плоскости
большую роль играет понятие площади
области. Простейшей областью, имеющей
площадь, является прямоугольник, площадь
которого равна произведению двух смежных
сторон. Понятие «площадь криволинейной
трапеции» вводилось при изучении
интеграла Римана по отрезку. Пусть
криволинейная трапеция имеет в основании
отрезок
,
лежащий на прямой
,
боковые ее стороны параллельны оси OY,
а четвертая сторона задается уравнением
где
непрерывна на
,
причем
.
Такую трапецию назовем выпуклой в
направлении оси OY,
ее площадь равна
.
Криволинейную трапецию, имеющую в
основании отрезок
,
лежащий на прямой
,
с боковыми сторонами параллельными оси
OX
и четвертой стороной, заданной уравнением
где
непрерывна и
при
,
назовем выпуклой в направлении оси OX.
Ее площадь равна
.
Квадрируемой областью будем называть область, которая после разрезов по конечному числу отрезков, параллельных осям координат, распадается на конечное число прямоугольников и криволинейных трапеций, выпуклых в направлении координатных осей. Площадь этой области равна сумме площадей входящих в нее прямоугольников и криволинейных трапеций. Все области и подобласти, рассматриваемые в разделе «Двойной интеграл» предполагаются квадрируемыми.
Задача о вычислении
объема цилиндроида.
Пусть в области
D
плоскости OXY
задана непрерывная функция
,
.
Рассмотрим лежащую выше плоскости
поверхность
.
Цилиндроидом,
выпуклым в направлении оси OZ
называется тело, ограниченное снизу
областью D,
лежащей на плоскости
,
сверху поверхностью
,
с
боков цилиндрической поверхностью с
образующими, параллельными оси OZ,
и направляющей – границей области D.
В данном случае мы имеем цилиндроид с
основанием, расположенном на плоскости
.
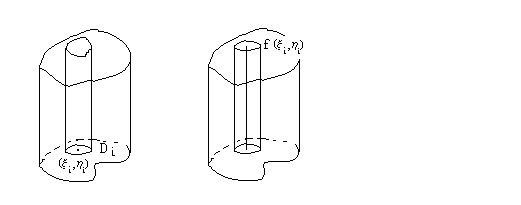
Область D
разобьем на n
квадрируемых частей с площадями
,
,
,…,
.
Получим n
подобластей
,
из которых состоит область D.
Через границу каждой области
проведем цилиндрическую поверхность
с образующими параллельными оси OZ.
Таких поверхностей будет n
.Они разобьют цилиндроид на n
частей. Возьмем i-ую
часть, основанием которой служит область
с площадью
.
Внутри этой части возьмем произвольную
точку
,
и вычислим значение
.
Рассмотрим
цилиндр, высота которого
,
а площадь основания равна
.
Этим цилиндром заменим i-ую
часть тела с основанием
.
Объем данного цилиндра равен
.
То же самое проделаем со всеми частями,
на которые мы разбили цилиндрическое
тело. Получим ступенчатое тело, состоящее
из n
цилиндров. Объем этого тела равен сумме
объемов цилиндров:
.
Диаметром
подобласти
назовем наибольше расстояние
между точками границы области (например,
диаметром прямоугольника будет длина
диагонали, диаметром круга будет
диаметр). Число
,
называемое диаметром разбиения, есть
наибольший из всех диаметров подобластей
,
на которые мы разбили область D.
Будем измельчать разбиение области D.
Это означает, что мы устремим число n
к бесконечности, и при этом
устремим к 0, так что все подобласти
стянутся в точки. При этом ступенчатое
тело, состоящее из n
цилиндров, по форме приблизится к
исходному цилиндроиду телу. Поэтому
за объем V
примем
предел
Определение двойного интеграла.
Пусть в области
D
плоскости OXY
задана функция
.
Функция
может принимать любые значения и может
не быть непрерывной. Область D
разобьем на n
подобластей
с площадями
Внутри i-ой
подобласти возьмем произвольную точку
в ней вычислим значение заданной функции
и умножим результат на
Проделав это со всеми подобластями
,
образуем сумму
Она называется
интегральной суммой для функции
по области D.
Если существует предел этой суммы при
n
стремящимся к бесконечности, и
стремящимся к 0, не зависящий ни от
способа разбиения области D
на подобласти, ни от выбора точек
,
то функция
называется интегрируемой по области
D,
а этот предел называется двойным
интегралом от функции
по области D
и обозначается
То есть двойной интеграл по определению равен
.
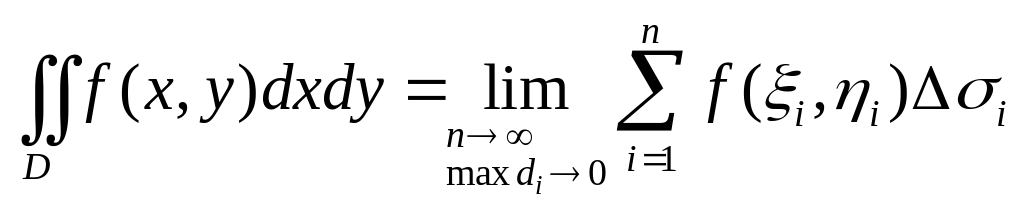Область D
называется областью интегрирования,
называется элементом площади;
называются переменными интегрирования,
- подынтегральной функцией. Очевидно,
что в случае, когда
имеем
,
где
–
площадь области D.
Любая непрерывная функция интегрируема по квадрируемой области D, но существуют также интегрируемые функции, не являющиеся непрерывными. Так, если функция имеет разрыв первого рода вдоль кривой, которая является участком границы квадрируемой подобласти области D, то также интегрируема по D.
Свойства двойного интеграла.
Из свойств сумм, свойств пределов, а также из определения двойного интеграла как предела интегральных сумм следуют свойства двойного интеграла.
Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от слагаемых функций
.
2. Постоянный множитель можно вынести за знак интеграла
3. Если
всюду в области D,
то
4. Если M и m есть соответственно наибольшее и наименьшее значения функции в области D, то
5. Если функция
непрерывная в замкнутой области D,
то в этой области найдется по крайней
мере одна точка
для которой справедливо равенство
где S площадь области D (теорема о среднем).
6. Если область
D
разбита на две квадрируемые части
и
,
то
Вычисление двойного интеграла.
Очевидно, что формула, определяющая двойной интеграл в виде предела интегральных сумм пригодна только для приближенных вычислений, если функция не является постоянной в области D. Для получения точного результата и использования формулы Ньютона-Лейбница, определяющей значение интеграла по отрезку в виде разности значений первообразной в конечных точках отрезка, двойной интеграл сводят к повторному интегралу.
Выведем формулу связи двойного интеграла с повторным для случая неотрицательной функции. Общий случай интегрируемой функции легко сводится к этому частному случаю путем разбиения области интегрирования на подобласти и использования интеграла от постоянной.
Итак, если
,
то двойной интеграл есть объем
соответствующего цилиндроида:
.
Рассмотрим
сначала случай, когда D
– прямоугольник
.
Вспомним формулу определения объема
тела по известным площадям поперечных
сечений
,
где
–
площадь поперечника, вырезаемого из
тела соответствующей плоскостью,
ортогональной оси OX.
В нашем случае таким поперечником
является криволинейная трапеция с
основанием
,
ограниченная сверху кривой
.
Следовательно,
.
В итоге,
.
Аналогичным образом, рассекая
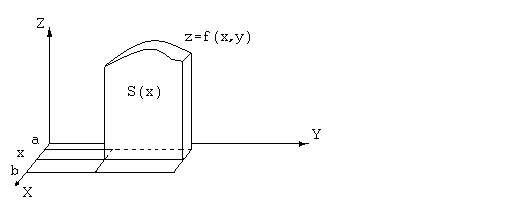
тело плоскостями,
ортогональными OY,
получим другое представление объема
того же цилиндроида:
.
Таким образом, в случае прямоугольной
области
.
Рассмотрим теперь более общий случай области, выпуклой в направлении оси OY. Это означает, что граница области D пересекается любой прямой параллельной оси OY либо не более, чем в двух точках, либо по одному отрезку.
Пусть область D
такова, что расположена между прямыми
параллельными оси OY.
Эти прямые касаются границы области D
или частично совпадают с границей по
отрезку.
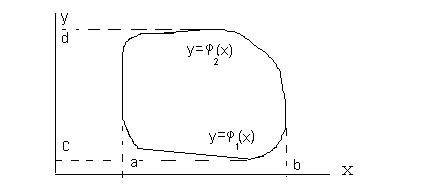
Участки границы
области D,
проецирующиеся на интервал
,
заданы уравнениями соответственно
и
,
.
Найдем
и
.
Таким образом, область D
находится внутри прямоугольника
.
Определим новую
функцию
следующим образом:
,
если
,
и
в остальных точках прямоугольника
.
Из свойств двойного интеграла следует,
что
.
Представляя двойной интеграл от
по прямоугольнику в виде повторного
интеграла, получим:
.
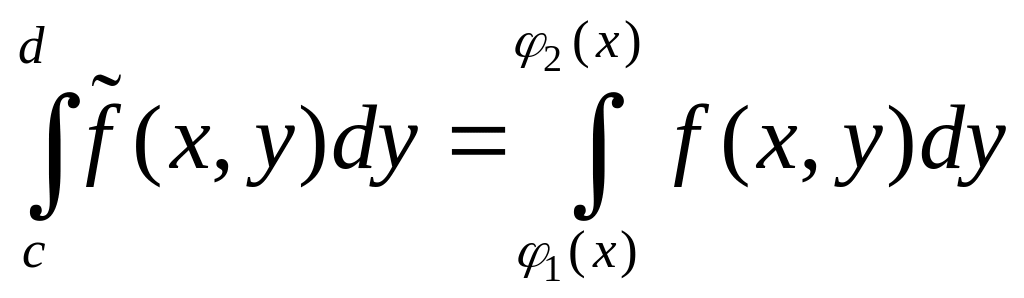Следовательно,
.
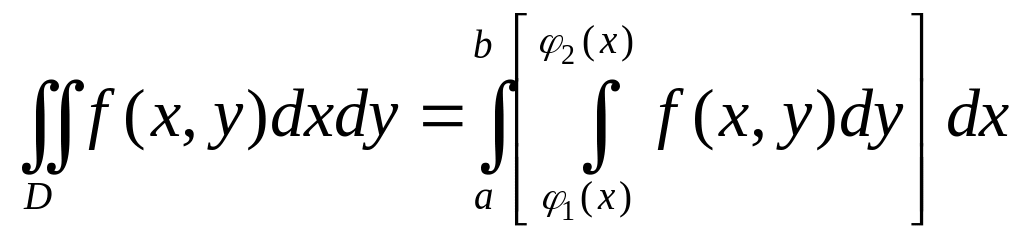Интеграл справа,
называемый повторным, обычно записывают
несколько по-другому, помещая
сразу после внешнего интеграла и опуская
квадратные скобки. В результате имеем
следующее выражение двойного интеграла
через повторный:
.
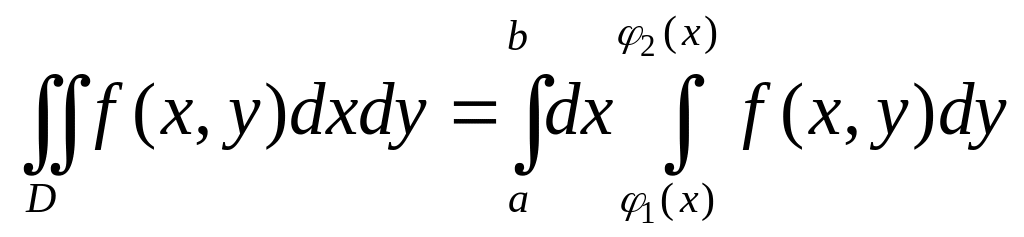Способ вычисления
повторного интеграла следующий. Сначала
вычисляется интеграл по
– внутренний интеграл, который берется
от функции
по переменной
,
когда
считается постоянной, с использованием
формулы Ньютона-Лейбница. Верхний и
нижний пределы внутреннего интеграла
зависят от
,
так что, взяв внутренний интеграл, мы
получим внешний интеграл по переменной
от полученной функции, зависящей от
.
Остается взять внешний интеграл, где
верхний и нижний пределы должны быть
константами.
Пределы
двукратного интеграла определяются по
виду области D,
исходя из чертежа. Определяется отрезок
на оси OX,
на который проецируется область D.
Определяются кривые
и
,
ограничивающие область D,
соответственно снизу и сверху. Функции
и
являются пределами для внутреннего
интеграла, взятого по
,
то есть,
,
есть ординаты точек входа и выхода из
области D
при движении по прямой, параллельной
оси OY,
в сторону увеличения
при фиксированном
.
Числа
и
–
нижний и верхний пределы внешнего
интеграла по
.
Аналогичная формула перехода к повторному интегралу справедлива для области, выпуклой в направлении оси OX, только в таком случае в повторном интеграле внутренним будет интеграл по переменной .
В случае произвольной квадрируемой области ее разбивают на конечное число выпуклых в направлении осей подобластей и применяют переход к повторному интегралу в каждой из этих подобластей.
П р и м е р ы.
1.Вычислить
по области
ограниченной линиями
Р е ш е н и е. Найдем
точки пересечения границ области D:
Прямая, проведенная
через область параллельно оси OY
в направлении роста
между прямыми
и
,
пересекает на точке входа параболу
а на точке выхода прямую
Внешними пределами (по
)
являются 0 и 1, а внутренними (по
)
и
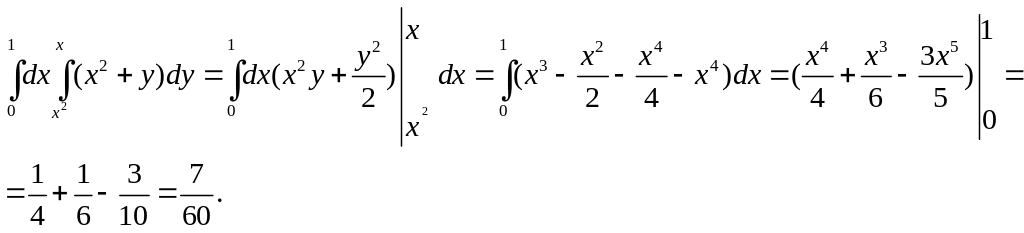
2. Вычислить
по области
Р е ш е н и е. Найдем
точки пересечения граничных кривых
области D.
Линии
и
пересекаются в точке (1,1). Линии
пересекаются
в точке (0,0). Линии
пересекаются в точке (2,0). Если вычислять
этот интеграл, взяв в качестве внешнего
интегрирования интегрирование по
,
то при определении пределов интегрирования
по
на выходе будут две разные линии, и
придется разбивать область интегрирования
на две области. Так что в этом случае
внешнее интегрирование берем по
,
а внутреннее по
.
Прямая, пересекающая область параллельно
оси
в положительном направлении, пересекает
в точке входа линию
а в точке выхода линию
Внешними пределами (по
)
будут 0 и 1, а внутренними пределами
(по
)
и
В
результате имеем
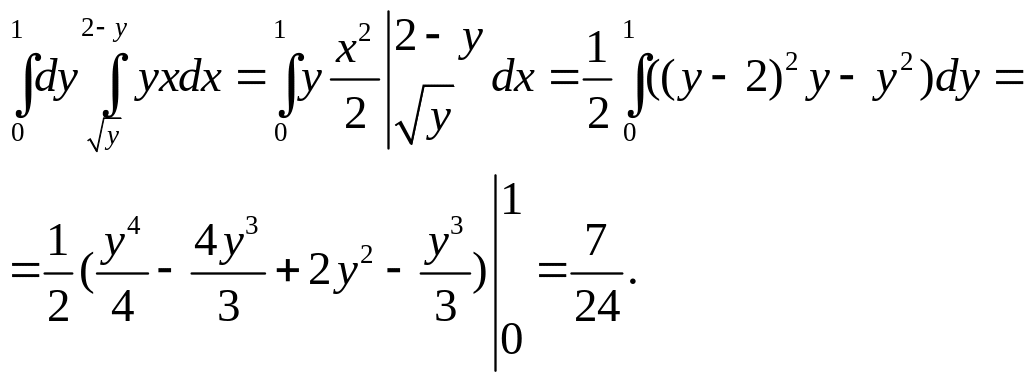
3. Вычислить
,
если область D
ограничена параболой
и прямой
.
Замена переменных в двойном интеграле.
Для успешного
вычисления двойного интеграла иногда
целесообразно производить замену
переменных, например, если сложная
область интегрирования D
в плоскости XOY
является образом прямоугольника
со
сторонами, параллельными координатным
осям в плоскости параметров UOV
при отображении
.
Будем предполагать, что функции
имеют непрерывные частные производные
первого порядка в
,
то есть отображение непрерывно
дифференцируемо, причем,
.
Возьмем малый
прямоугольник в
с вершинами
,
,
и
.
При отображении
,
вершины
переходят в точки
с координатами
,
,
и
.
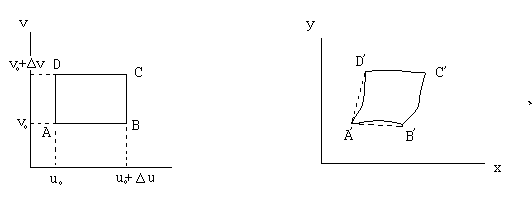
Если
малы, то вследствие непрерывной
дифференцируемости отображения образы
сторон прямоугольника мало отличаются
от прямых, а область
близка к параллелограмму, построенному
на векторах
,
.
Воспользуемся формулой конечных приращений Лагранжа и запишем
,
,
где
Сосчитаем площадь параллелограмма
как модуль векторного произведения
векторов
и
:
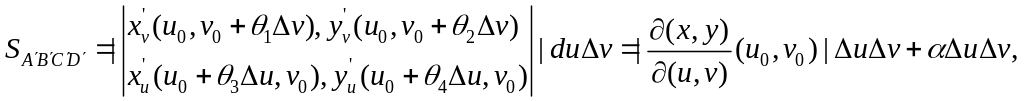
где
–
бесконечно малая величина при
.
Пусть теперь
прямоугольник
в плоскости UOV
разбит прямыми, параллельными осям, на
малых
прямоугольников
со сторонами
.
При этом область D
в плоскости XOY
разобьется на подобласти
близкие к параллелограммам.
Подсчитаем сумму площадей этих подобластей то есть площадь области D. В соответствии с полученной выше формулой площадь D равна
,
где
–
вершины прямоугольников
,
и
, если диаметр разбиения стремится к
нулю. Поскольку
,
где
–
площадь прямоугольника
,
мы можем получить точное значение
,
измельчая разбиения
и переходя к пределу в предыдущем
выражении для
.
Заметим, что первое слагаемое в этом
выражении является интегральной суммой
для непрерывной в
функции
,
а второе стремится к нулю при измельчении
разбиений. Таким образом,
,
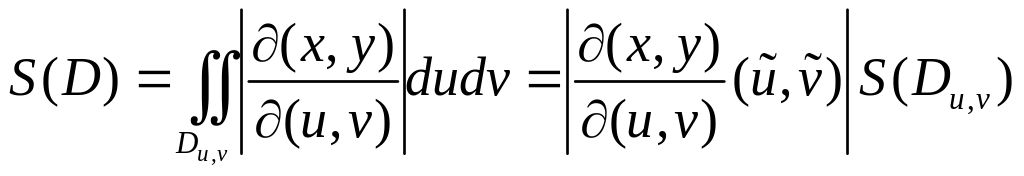где
.
Построим теперь
интегральную сумму для произвольной
интегрируемой по D
функции
для уже рассмотренного разбиения
области D
на прямоугольники
.
При этом, согласно полученной формуле
для площади области в плоскости XOY,
площадь каждой подобласти
равна
,
где
.
Выберем на каждой подобласти
точку
.
Это возможно, так как вследствие
интегрируемости функции мы можем
выбирать произвольную точку на подобласти
.
В результате интегральная сумма для
получения интеграла
равна
,
и представляет
собой интегральную сумму для функции
по прямоугольнику
.
Очевидно, что диаметры разбиений
и D
одновременно стремятся к нулю в силу
непрерывности отображения
.
Поэтому
.
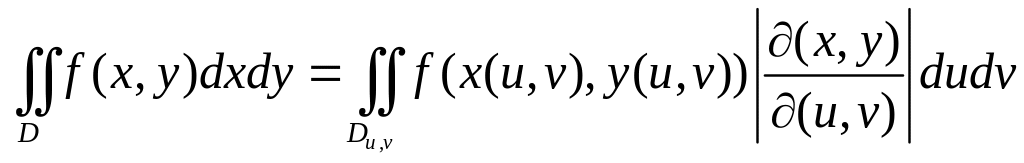П р и м е р ы.
1. Вычислить интеграл
по круговому
сектору , ограниченному линиями
Р е ш е н и е.
Применение декартовых координат в
данном случае было бы сложным. Перейдем
к полярным координатам
по формулам
Тогда в
плоскости полярных координат
имеем
прямоугольник, ограниченный прямыми
.
Вычислим
модуль
якобиана преобразования:
Таким образом,
.
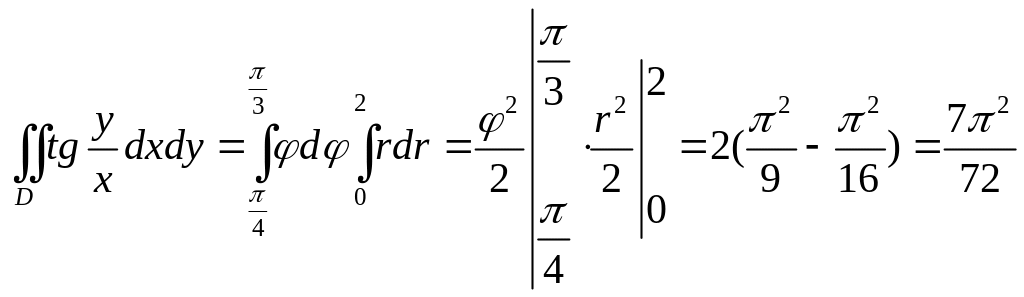2. Вычислить интеграл
по области
ограниченной
линиями
Р е ш е н и е. Для
упрощения вычисления перейдем к новым
переменным
Вычислим
модуль якобиана преобразования:
.
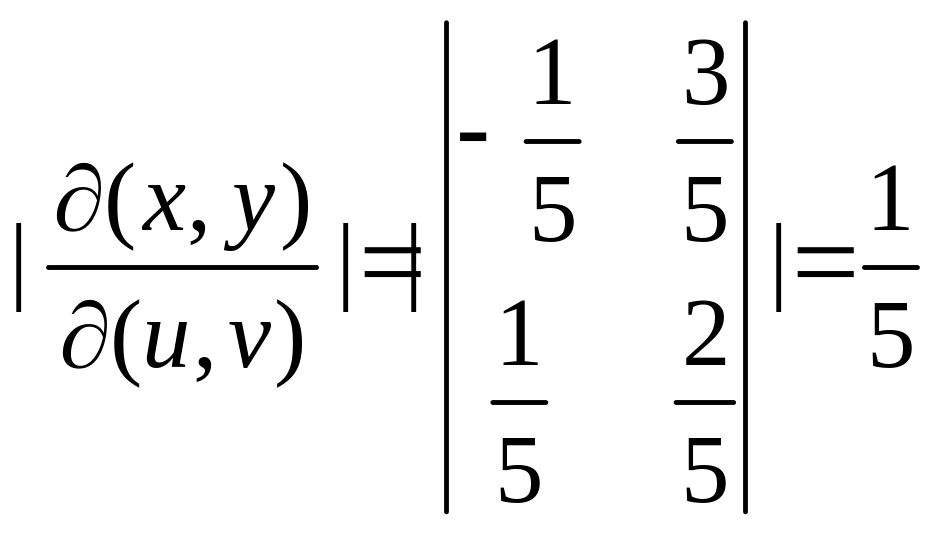Областью
интегрирования в плоскости новых
переменных будет прямоугольник со
сторонами, параллельными осям
и
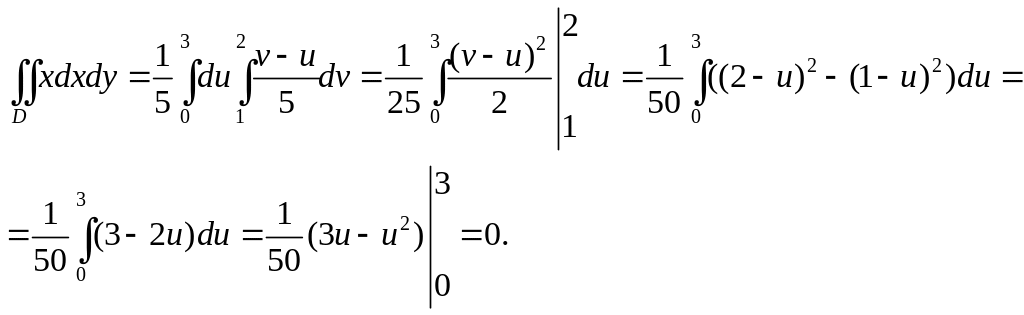
3. Вычислить
,
если область D
ограничена кривой
и прямыми
,
с помощью следующей замены переменных:
.
Приложения двойного интеграла к вычислению площади поверхности.
Прежде всего, мы должны пояснить, что понимается под площадью поверхности, так как раньше понятие площадь относилось только к плоской области.
Пусть поверхность
S
задается соотношением
,
где
–
квадрируемая область в плоскости XOY.
Функция
задает взаимнооднозначное соответствие
между точками области
и точками поверхности S.
Пусть функция
имеет непрерывные производные первого
порядка, то есть непрерывно дифференцируема
в
.
В этом случае поверхность является
гладкой, то есть в каждой ее точке
можно провести касательную плоскость
с нормалью, задаваемой вектором
.
Разобьем область
на квадрируемые подобласти
.
Проведем цилиндрические поверхности
с образующими, ортогональными плоскости
XOY
и направляющими – границами
.
Эти цилиндрические поверхности разобьют
исходную поверхность на фрагменты
.
Выберем произвольную точку
на каждом фрагменте
и проведем касательную плоскость к
поверхности S
в точке
.
Нормаль к этой плоскости
.
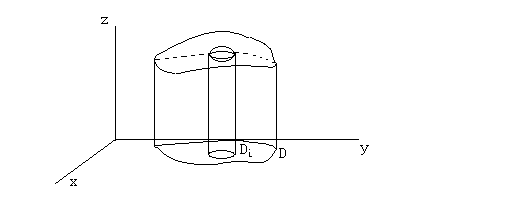
Та же цилиндрическая
поверхность, которая вырезала фрагмент
из поверхности S,
вырежет фрагмент
из касательной плоскости к фрагменту
.
Подсчитаем площадь каждого плоского
фрагмента
и просуммируем полученные площади. Если
теперь измельчать разбиение области
,
устремляя количество подобластей
к бесконечности и одновременно устремляя
диаметр разбиения к нулю, сумма площадей
плоских фрагментов
будет стремиться к пределу, который мы
и назовем площадью поверхности S.
Прежде, чем мы
выведем формулу площади поверхности,
найдем связь между площадью подобласти
и
площадью части касательной плоскости
,
проецирующейся на
.
Рассмотрим плоскость, расположенную
под углом
к плоскости XOY
так, что нормаль к наклонной плоскости
и ось OZ
лежат в плоскости Q
и составляют между собой угол
.
Пусть прямоугольник
со сторонами длин
и
расположен на наклонной плоскости так,
что одна его сторона (длины
)
ортогональна плоскости Q,
а другая (длины
)
параллельна плоскости Q.
Проекцией прямоугольника
на плоскость XOY
является прямоугольник
со сторонами
и
.
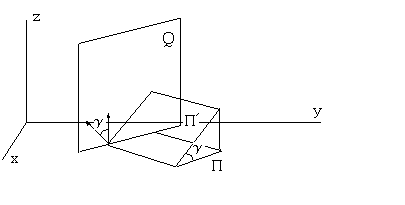
Таким образом,
площадь прямоугольника
равна площади прямоугольника
,
деленной на
.
Площадь
квадрируемой области
можно
получить, разбивая
системой ортогональных прямых на
прямоугольники, суммируя площади этих
прямоугольников и переходя к пределу
при измельчении разбиения. Соответствующим
образом получается и площадь области
,
проецирующейся на
.
Следовательно, площадь
равна разделенной на
площади
,
где
–
угол, который нормаль
составляет
с осью OZ.
Значение
легко получить, используя формулу
скалярного произведения:
.
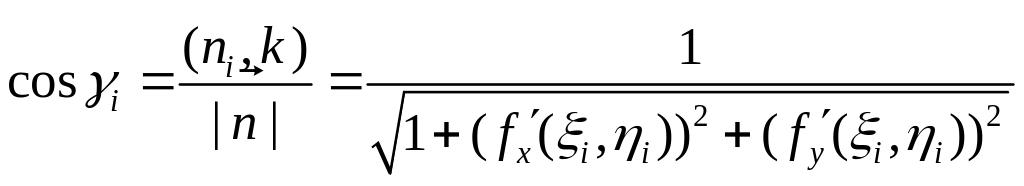Итак, для
вычисления площади поверхности S
просуммируем площади всех плоских
областей
обозначая площади
через
:
.
Очевидно, что
полученная сумма есть интегральная
сумма от функции
по области
,
на которую проецируется поверхность
S.
Переходя к пределу при увеличении
и стремлении диаметра разбиения к нулю,
получим в соответствии с определением
площадь поверхности
:
.
(ПП)
Для поверхностей,
задаваемых в виде
или
формулы вычисления площади поверхности
аналогичны. К сожалению, не все поверхности
удобно задавать в явном виде – когда
одна из переменных выражается через
остальные. Часто поверхности задаются
в параметрическом виде:
.
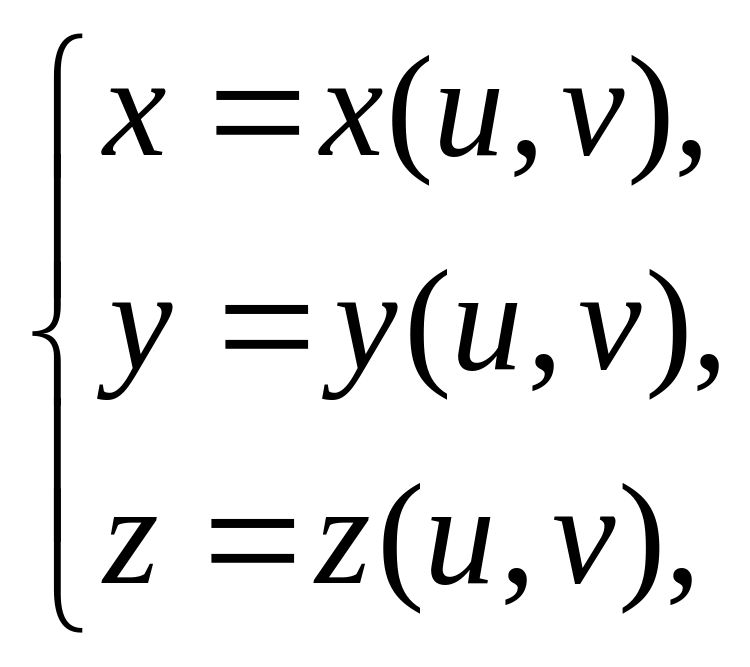
Выведем формулу
для получения площади поверхности,
заданной параметрически. Предположим,
что функции
и
имеют непрерывные производные первого
порядка по обеим переменным при
,
причем
.
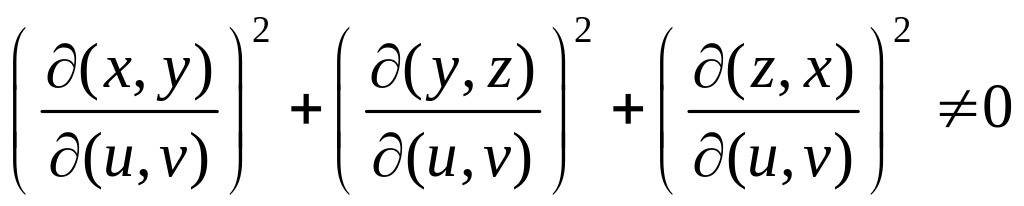Последнее
неравенство означает, что в окрестности
любой точки
можно построить хотя бы одно из
обратных отображений:
или
вследствие отличия от нуля соответствующего
якобиана. Предположим, что
в
окрестности точки
,
и мы построили обратное отображение
.
Тогда в окрестности точки
,
где
мы имеем явную зависимость
,
где
.
Поэтому для вычисления площади
соответствующего фрагмента поверхности
можно воспользоваться полученной выше
формулой площади поверхности (ПП). Для
этого следует выразить
и
через заданные параметрические
зависимости. Решая систему уравнений
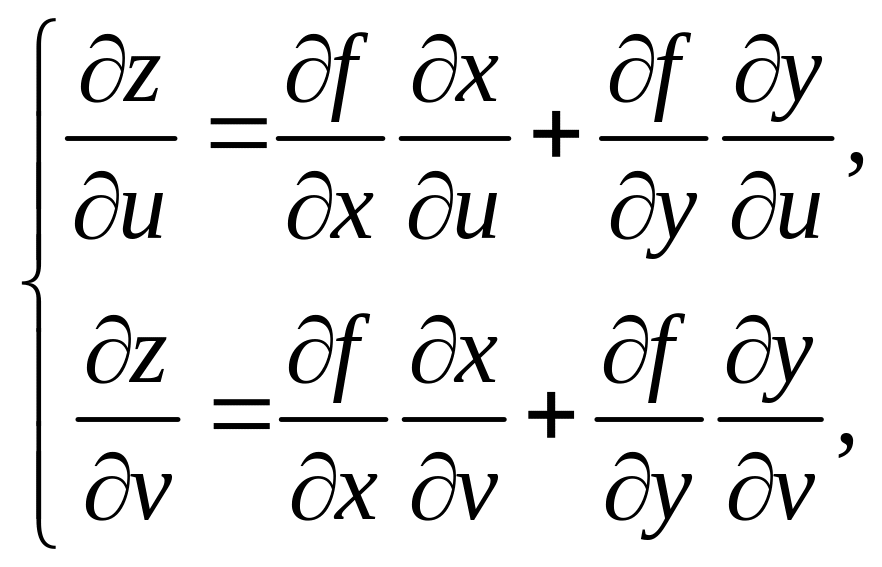относительно
и
,
найдем:
,
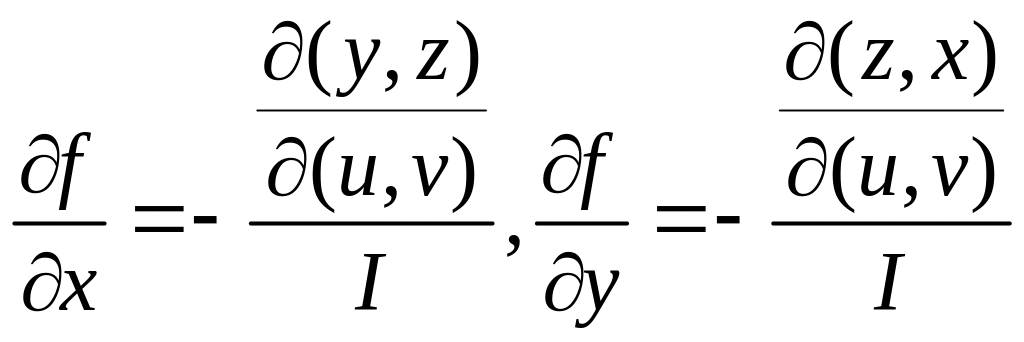где
.
Переходя в формуле (ПП) к новым переменным
,
получим
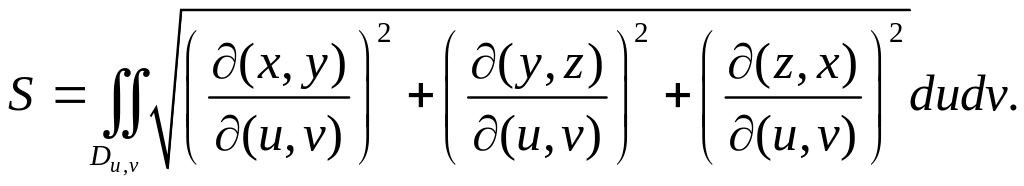(ППП)
Здесь мы получили сразу площадь всей поверхности, хотя собирались получить площадь того фрагмента, где получено явное выражение . Однако, разбивая поверхность на фрагменты, на каждом из которых одна из трех декартовых координат явно выражается через две другие и переходя к переменным в выражении площади каждого такого фрагмента, мы получим одинаковые подынтегральные выражения для различных фрагментов области значений параметров . Останется только сложить эти площади.
П р и м е р.
Вычислить площадь
боковой поверхности конуса
,
отсеченной плоскостью
.
Р е ш е н и е 1. Введем параметризацию:
.
Вычислим якобианы:
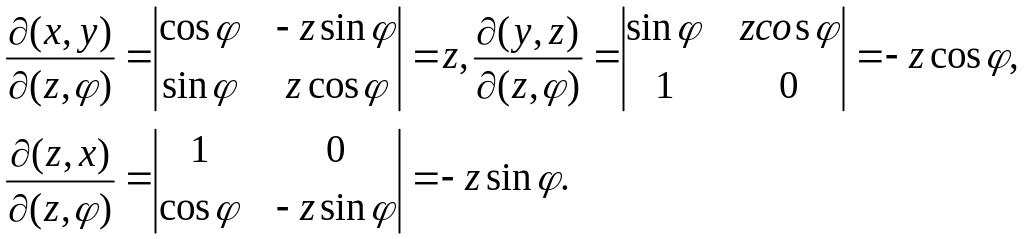
Применяя формулу (ППП), получим
.
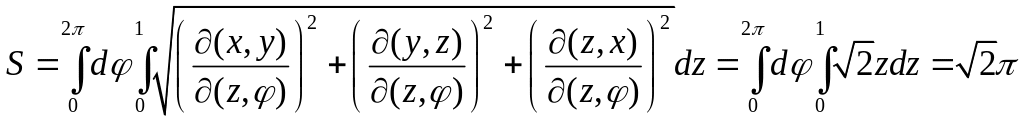Р е ш е н и е 2.
Вычислим площадь той же поверхности,
по формуле (ПП) для случая явного задания
поверхности. Проекцией конуса на
плоскость XOY
, то есть, областью
является круг
,
так как плоскость
пересекается с конусом по окружности,
проецирующейся на единичную окружность
в плоскости XOY.
Поскольку в данном случае
найдем частные производные:
.
Применяя формулу (ПП), получим
,
так как интеграл представляет собой
умноженную на
площадь
области
– круга единичного радиуса.
2. Найти площадь
поверхности тора
,
.